Tes mann–whitney u
Uji Mann-Whitney U (terkadang disebut uji jumlah peringkat Wilcoxon) digunakan untuk membandingkan perbedaan antara dua sampel independen ketika distribusi sampel tidak terdistribusi normal dan ukuran sampel kecil (n <30).
Uji ini dianggap setara dengan uji t dua sampel independen .
Berikut beberapa contoh kapan Anda dapat menggunakan tes Mann-Whitney U:
- Anda ingin membandingkan gaji lima lulusan universitas A dengan gaji lima lulusan universitas B. Gaji tidak terdistribusi secara normal.
- Anda ingin mengetahui apakah penurunan berat badan bervariasi untuk dua kelompok: 12 orang yang menggunakan diet A dan 10 orang yang menggunakan diet B. Penurunan berat badan tidak terdistribusi secara normal.
- Ingin diketahui apakah nilai 8 siswa di kelas A berbeda dengan nilai 7 siswa di kelas B. Nilai tersebut tidak berdistribusi normal.
Dalam setiap contoh, Anda ingin membandingkan dua kelompok, distribusi sampelnya tidak normal, dan ukuran sampelnya kecil.
Dengan demikian, uji Mann-Whitney U dapat dilakukan sepanjang asumsi berikut terpenuhi.
Asumsi Uji Mann-Whitney U
Sebelum melakukan tes Mann-Whitney U, Anda harus memastikan bahwa empat asumsi berikut terpenuhi:
- Biasa atau kontinu: Variabel yang Anda analisis bersifat ordinal atau kontinu. Contoh variabel ordinal mencakup item Likert (misalnya, skala 5 poin yang berkisar dari “sangat tidak setuju” hingga “sangat setuju”). Contoh variabel kontinu mencakup tinggi badan (diukur dalam inci), berat badan (diukur dalam pon), atau nilai ujian (diukur dari 0 hingga 100).
- Independensi: Semua observasi dari kedua kelompok tidak bergantung satu sama lain.
- Bentuk: Bentuk sebaran kedua kelompok kurang lebih sama.
Jika asumsi tersebut terpenuhi, maka dapat dilakukan uji Mann-Whitney U.
Cara Melakukan Tes Mann-Whitney U
Untuk melakukan uji Mann-Whitney U, kami mengikuti prosedur pengujian hipotesis lima langkah standar :
1. Nyatakan asumsinya.
Dalam kebanyakan kasus, uji Mann-Whitney U dilakukan sebagai uji dua sisi. Hipotesis nol dan hipotesis alternatif ditulis dalam bentuk:
H 0 : Kedua populasi sama
H a : Kedua populasi tersebut tidak sama
2. Tentukan tingkat signifikansi yang akan digunakan dalam hipotesis.
Tentukan tingkat signifikansinya. Pilihan umum adalah .01, .05, dan .1.
3. Temukan statistik pengujian.
Statistik uji dilambangkan dengan U dan merupakan yang lebih kecil dari U 1 dan U 2 , sebagaimana didefinisikan di bawah ini:
kamu 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
kamu 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
dimana n 1 dan n 2 masing-masing adalah ukuran sampel untuk sampel 1 dan 2, dan R 1 dan R 2 adalah jumlah peringkat masing-masing sampel 1 dan 2.
Contoh di bawah ini akan menunjukkan cara menemukan statistik pengujian ini secara detail.
4. Menolak atau tidak menolak hipotesis nol.
Dengan menggunakan statistik uji, tentukan apakah Anda dapat menolak hipotesis nol berdasarkan tingkat signifikansi dan nilai kritis yang terdapat pada tabel Mann-Whitney U.
5. Interpretasikan hasilnya.
Interpretasikan hasil tes dalam konteks pertanyaan yang diajukan.
Contoh melakukan tes Mann-Whitney U
Contoh berikut menunjukkan cara melakukan tes Mann-Whitney U.
Contoh 1
Kami ingin tahu apakah pengobatan baru efektif dalam mencegah serangan panik. Sebanyak 12 pasien dibagi secara acak menjadi dua kelompok yang terdiri dari 6 orang dan ditugaskan untuk menerima obat baru atau plasebo. Pasien kemudian mencatat jumlah serangan panik yang mereka alami selama sebulan.
Hasilnya ditunjukkan di bawah ini:
| OBAT BARU | PLACEBO |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
Lakukan tes Mann-Whitney U untuk melihat apakah terdapat perbedaan jumlah serangan panik pada pasien kelompok plasebo dibandingkan dengan kelompok obat baru. Gunakan tingkat signifikansi 0,05.
1. Nyatakan asumsinya.
H 0 : Kedua populasi sama
H a : Kedua populasi tersebut tidak sama
2. Tentukan tingkat signifikansi yang akan digunakan dalam hipotesis.
Masalahnya memberitahu kita bahwa kita harus menggunakan tingkat signifikansi 0,05.
3. Temukan statistik pengujian.
Ingatlah bahwa statistik uji dilambangkan dengan U dan merupakan yang lebih kecil dari U 1 dan U 2 , sebagaimana didefinisikan di bawah:
kamu 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
kamu 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
dimana n 1 dan n 2 masing-masing adalah ukuran sampel untuk sampel 1 dan 2, dan R 1 dan R 2 adalah jumlah peringkat masing-masing sampel 1 dan 2.
Untuk mencari R 1 dan R 2 , kita perlu menggabungkan pengamatan dari kedua kelompok dan mengurutkannya dari yang terkecil hingga yang terbesar:
| OBAT BARU | PLACEBO |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
Jumlah sampel: 1 , 1 , 2 , 3 , 3 , 4 , 4 , 5 , 5 , 6 , 8 , 9
Peringkat: 1.5 , 1.5 , 3 , 4.5 , 4.5 , 6.5 , 6.5 , 8.5 , 8.5 , 10 , 11 , 12
R 1 = jumlah rangking sampel 1 = 1,5+4,5+4,5+6,5+8,5+8,5 = 34
R 2 = jumlah rangking sampel 2 = 1,5+3+6,5+10+11+12 = 44
Selanjutnya, kita menggunakan ukuran sampel kita n 1 dan n 2 serta jumlah peringkat kita R 1 dan R 2 untuk mencari U 1 dan U 2 .
U1 = 6(6) + 6(6+1)/2 – 34 = 23
U2 = 6(6) + 6(6+1)/2 – 44 = 13
Statistik pengujian kami adalah yang lebih kecil dari U1 dan U2 , yang kebetulan adalah U=13.
Catatan: Kita juga dapat menggunakan kalkulator tes Mann-Whitney U untuk menentukan bahwa U = 13.
4. Menolak atau tidak menolak hipotesis nol.
Menggunakan n 1 = 6 dan n 2 = 6 dengan tingkat signifikansi 0,05, tabel Mann-Whitney U memberi tahu kita bahwa nilai kritisnya adalah 5:
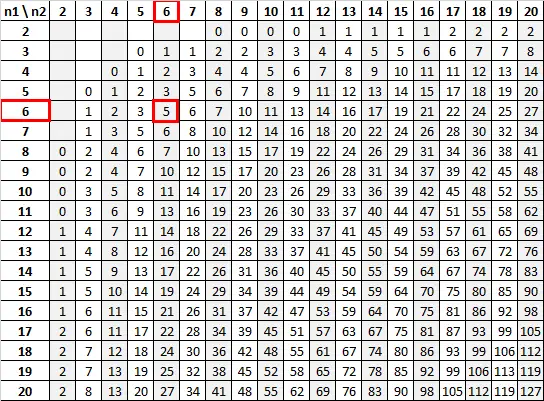
Karena statistik pengujian kami (13) lebih besar dari nilai kritis kami (5), kami gagal menolak hipotesis nol.
5. Interpretasikan hasilnya.
Karena kami gagal menolak hipotesis nol, kami tidak memiliki cukup bukti untuk mengatakan bahwa jumlah serangan panik yang dialami pasien pada kelompok plasebo berbeda dengan jumlah serangan panik pada kelompok obat baru.
Contoh 2
Kami ingin tahu apakah belajar 30 menit sehari selama seminggu membantu siswa berprestasi lebih baik dalam ujian. Sebanyak 15 pasien secara acak ditugaskan untuk belajar atau tidak ada kelompok belajar. Setelah seminggu, semua siswa mengikuti tes yang sama.
Hasil tes untuk kedua kelompok ditunjukkan di bawah ini:
| BELAJAR | TIDAK BELAJAR |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
Lakukan tes Mann-Whitney U untuk melihat apakah ada perbedaan nilai tes kelompok belajar dibandingkan dengan kelompok tidak belajar. Gunakan tingkat signifikansi 0,01.
1. Nyatakan asumsinya.
H 0 : Kedua populasi sama
H a : Kedua populasi tersebut tidak sama
2. Tentukan tingkat signifikansi yang akan digunakan dalam hipotesis.
Masalahnya memberitahu kita bahwa kita harus menggunakan tingkat signifikansi 0,01.
3. Temukan statistik pengujian.
Ingatlah bahwa statistik uji dilambangkan dengan U dan merupakan yang lebih kecil dari U 1 dan U 2 , sebagaimana didefinisikan di bawah:
kamu 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
kamu 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
dimana n 1 dan n 2 masing-masing adalah ukuran sampel untuk sampel 1 dan 2, dan R 1 dan R 2 adalah jumlah peringkat masing-masing sampel 1 dan 2.
Untuk mencari R 1 dan R 2 , kita perlu menggabungkan pengamatan dari kedua kelompok dan mengurutkannya dari yang terkecil hingga yang terbesar:
| BELAJAR | TIDAK BELAJAR |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
Jumlah sampel: 72 , 75 , 80 , 81, 84, 88 , 89 , 90 , 91 , 92 , 93 , 94 , 95 , 96 , 99
Baris: 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
R 1 = jumlah rangking sampel 1 = 5+7+8+9+10+12+14+15 = 80
R 2 = jumlah rangking sampel 2 = 1+2+3+4+6+11+13 = 40
Selanjutnya, kita menggunakan ukuran sampel kita n 1 dan n 2 serta jumlah peringkat kita R 1 dan R 2 untuk mencari U 1 dan U 2 .
U1 = 8(7) + 8(8+1)/2 – 80 = 12
U2 = 8(7) + 7(7+1)/2 – 40 = 44
Statistik pengujian kami adalah yang lebih kecil dari U1 dan U2 , yang kebetulan adalah U=12.
Catatan: Kita juga dapat menggunakan kalkulator uji Mann-Whitney U untuk menentukan bahwa U = 12.
4. Menolak atau tidak menolak hipotesis nol.
Menggunakan n 1 = 8 dan n 2 = 7 dengan tingkat signifikansi 0,01, tabel Mann-Whitney U memberi tahu kita bahwa nilai kritisnya adalah 6:
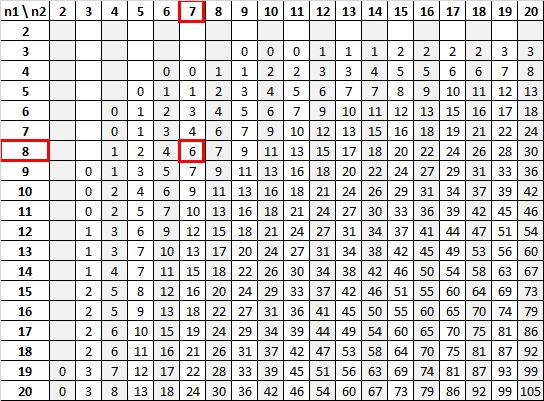
Karena statistik pengujian kami (12) lebih besar dari nilai kritis kami (6), kami gagal menolak hipotesis nol.
5. Interpretasikan hasilnya.
Karena kami gagal menolak hipotesis nol, kami tidak mempunyai cukup bukti untuk mengatakan bahwa nilai ujian siswa yang belajar berbeda dengan siswa yang tidak belajar.
Sumber daya tambahan
Kalkulator Tes Mann-Whitney U
Tabel Mann-Whitney U
Cara Melakukan Tes Mann-Whitney U di Excel
Cara melakukan tes Mann-Whitney U di R
Cara Melakukan Tes Mann-Whitney U dengan Python
Cara Melakukan Tes Mann-Whitney U di SPSS
Cara melakukan tes Mann-Whitney U di Stata