Matriks kovarians

Oleh Benjamin anderson Agustus 5, 2023 Statistik 0 Komentar

Artikel ini menjelaskan apa itu matriks kovarians dan apa rumusnya. Anda akan menemukan cara membuat matriks kovarians dengan contoh nyata dan sifat-sifat matriks kovarians.

Apa yang dimaksud dengan matriks kovarians?

Matriks kovarians merupakan matriks persegi yang elemen-elemennya merupakan varians dan kovarians dari variabel yang diteliti. Jadi, elemen diagonal utama matriks kovarians adalah varians setiap variabel, dan elemen sisanya adalah kovarians antar variabel.

Dalam statistik, matriks kovarians digunakan untuk menganalisis hubungan antara dua atau lebih variabel acak. Matriks kovarians sangat berguna karena memungkinkan Anda menafsirkan korelasi antara banyak variabel dengan cepat, karena Anda dapat melihat nilai semua kovarians variabel secara bersamaan.

Simbol matriks kovarians adalah huruf kapital Yunani sigma (Σ).

Cara menghitung matriks kovarians

Untuk menghitung matriks kovarians beberapa variabel statistik, harus dilakukan langkah-langkah sebagai berikut:

Hitung varians semua variabel.
Hitung kovarians setiap pasangan variabel.
Bentuk matriks kovarians:

Varians variabel i harus ditempatkan pada diagonal utama matriks, lebih tepatnya pada posisi i,i .
Kovariansi antara variabel i dan j harus diletakkan pada posisi i,j matriks.

Oleh karena itu, rumus matriks kovarians adalah sebagai berikut:

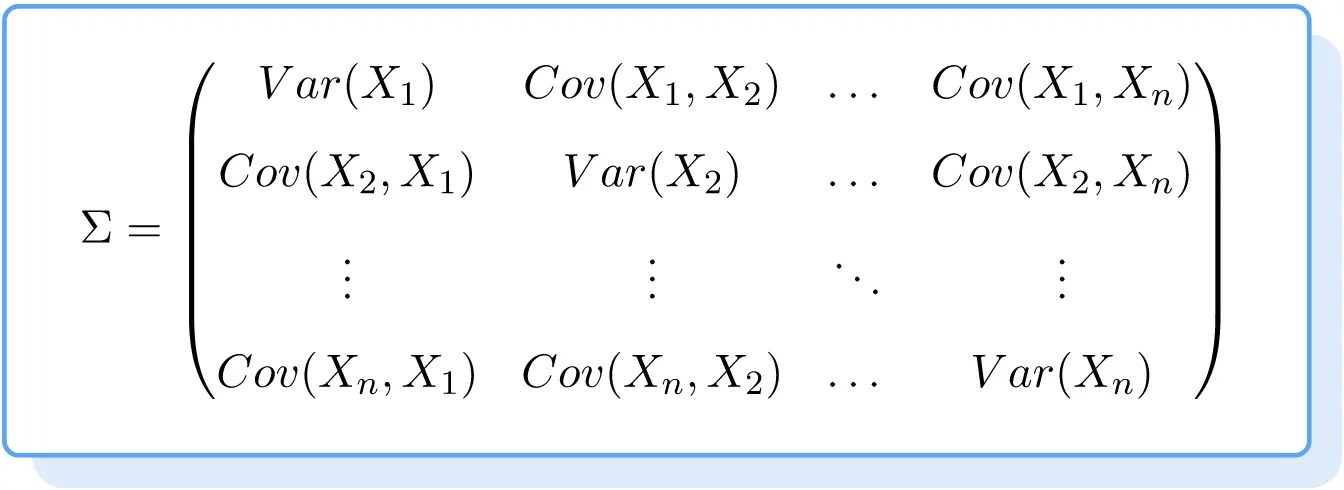
Contoh Matriks Kovariansi

Setelah melihat definisi matriks kovarians, berikut langkah-langkah latihannya agar Anda dapat melihat cara pembuatan matriks jenis ini.

Menghitung matriks kovarians variabel X, Y dan Z yang nilainya adalah:

X: 4, 7, 12, 5, 7
Dan: 9, 15, 19, 6, 8
Z: 7, 2, 4, 6, 3

Hal pertama yang perlu kita lakukan adalah menentukan varians semua variabel:

$Var(X)=7,6$

$Var(Y)=23,44$

$Var(Z)=3,44$

➤ Lihat: kalkulator kesenjangan

Kedua, kita mencari kovarians antara setiap pasangan variabel:

$Cov(X,Y)=11,2$

$Cov(X,Z)=-2,6$

$Cov(Y,Z)=-4,36$

➤ Lihat: kalkulator kovarians

Dan setelah kita menghitung semua varian dan kovarians, yang tersisa hanyalah membuat matriks kovarians. Untuk melakukan ini, kami menempatkan nilai varians pada diagonal utama matriks dan nilai kovarians pada posisinya yang sesuai:

$\Sigma=\begin{pmatrix}Var(X)&Cov(X,Y)&Cov(X,Z)\\[1.5ex]Cov(Y,X)&Var(Y)&Cov(Y,Z)\\[1.5ex]Cov(Z,X)&Cov(Z,Y)&Var(Z)\end{pmatrix}$

$\Sigma=\begin{pmatrix}7,6&11,2&-2,6\\[1.5ex]11,2&23,44&-4,36\\[1.5ex]-2,6&-4,36&3,44\end{pmatrix}$

Seperti yang Anda lihat, dengan merepresentasikan varians dan kovarians dalam sebuah matriks, interpretasi variabel menjadi sangat mudah. Variabel yang mempunyai dispersi paling besar adalah Y (23,44), sebaliknya variabel X dan Y mempunyai hubungan searah, sedangkan variabel X dan Z (berarti Y dan Z) mempunyai hubungan berbanding terbalik.

Perhatikan bahwa matriks kovarians selalu simetris, karena kovarians antara dua variabel tidak bergantung pada urutan variabel. Misalnya,

$Cov(X,Y)$

adalah sama dengan

$Cov(Y,X).$

Selain itu, matriks kovarians akan selalu berupa matriks persegi dan dimensinya akan sama dengan jumlah variabel. Dalam hal ini kita memiliki tiga variabel dan itulah mengapa matriksnya berukuran 3×3, tetapi jika kita hanya memiliki dua variabel, matriks kovariansnya akan menjadi 2×2.

Sifat-sifat matriks kovarians

Matriks kovarians memiliki ciri-ciri sebagai berikut:

Matriks kovarians merupakan matriks persegi yang orde banyaknya variabelnya.
Matriks kovarians bersifat simetris, artinya diagonal utama matriks tersebut merupakan sumbu simetri.
Matriks kovarians selalu bersifat semi-pasti positif.
Penentu matriks kovarians sama dengan atau lebih besar dari nol.

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya