Cara membuat matriks korelasi di spss

Matriks korelasi adalah tabel persegi yang menunjukkan koefisien korelasi Pearson antara berbagai variabel dalam suatu kumpulan data.

Sekadar mengingatkan, koefisien korelasi Pearson adalah ukuran hubungan linier antara dua variabel . Dibutuhkan nilai antara -1 dan 1 di mana:

• -1 menunjukkan korelasi linier negatif sempurna antara dua variabel
• 0 menunjukkan tidak ada korelasi linier antara dua variabel
• Angka 1 menunjukkan korelasi linier positif sempurna antara dua variabel

Semakin jauh koefisien korelasi dari nol maka semakin kuat hubungan kedua variabel tersebut.

Tutorial ini menjelaskan cara membuat dan menginterpretasikan matriks korelasi di SPSS.

Contoh : Cara Membuat Matriks Korelasi di SPSS

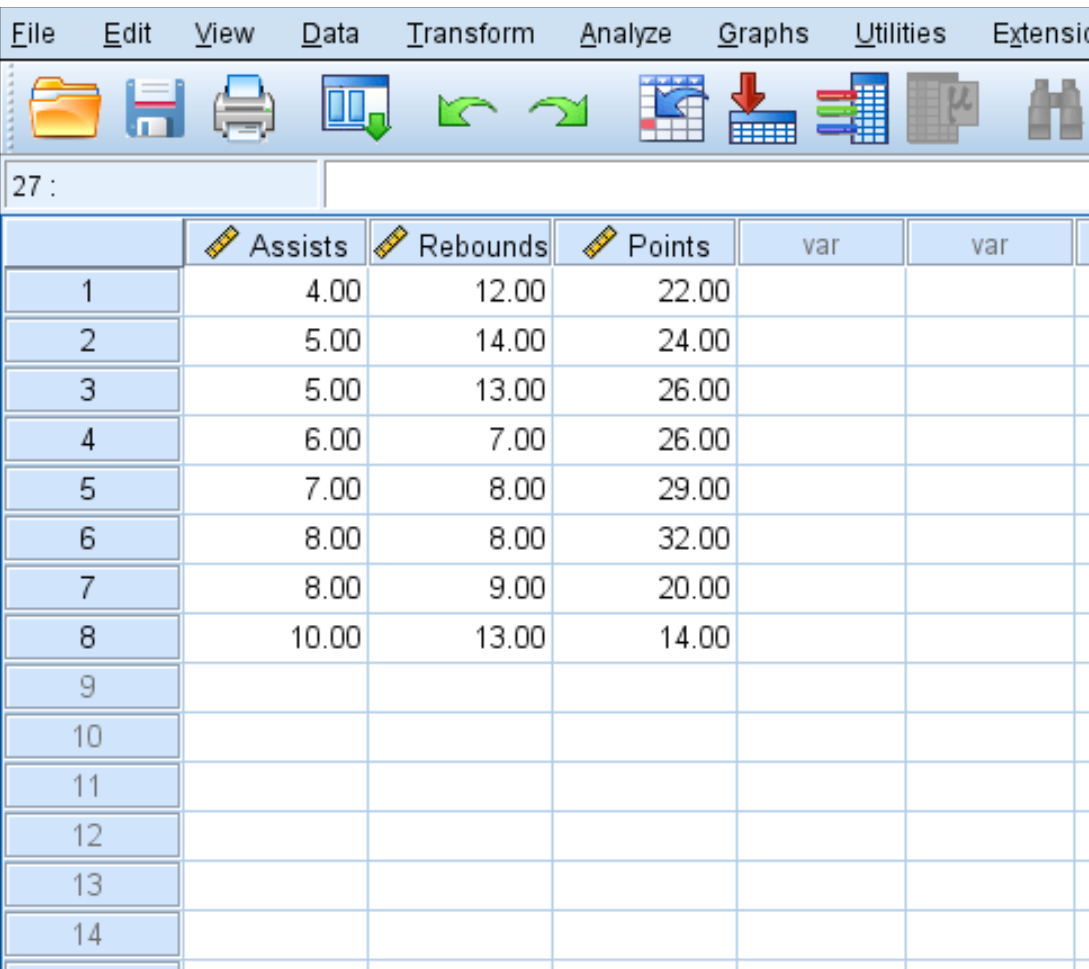
Ikuti langkah-langkah berikut untuk membuat matriks korelasi untuk kumpulan data ini yang menampilkan rata-rata assist, rebound, dan poin dari delapan pemain bola basket:

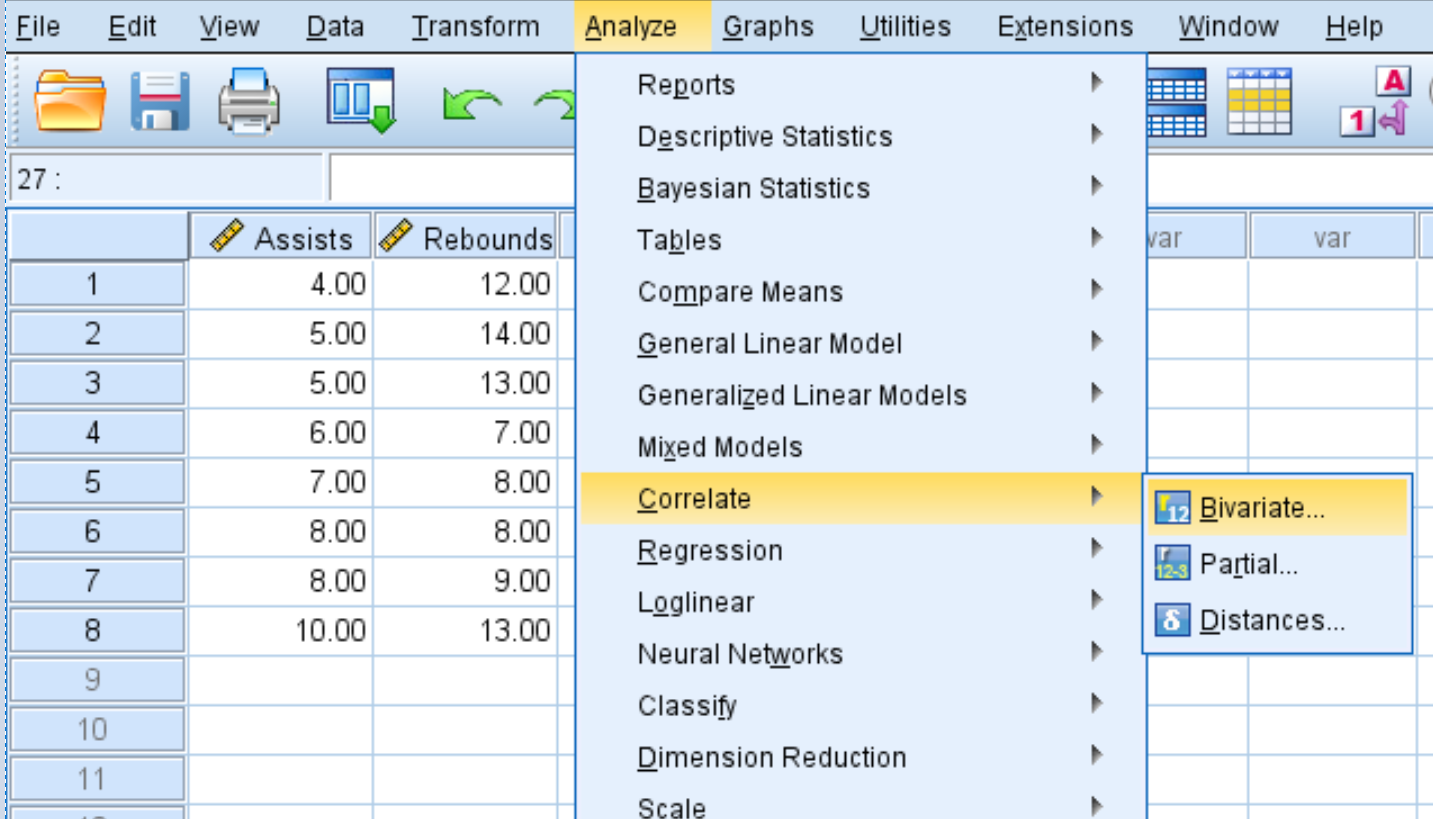
Langkah 1: Pilih Korelasi Bivariat.

• Klik tab Analisis .
• Klik Korelasi .
• Klik Bivariat .

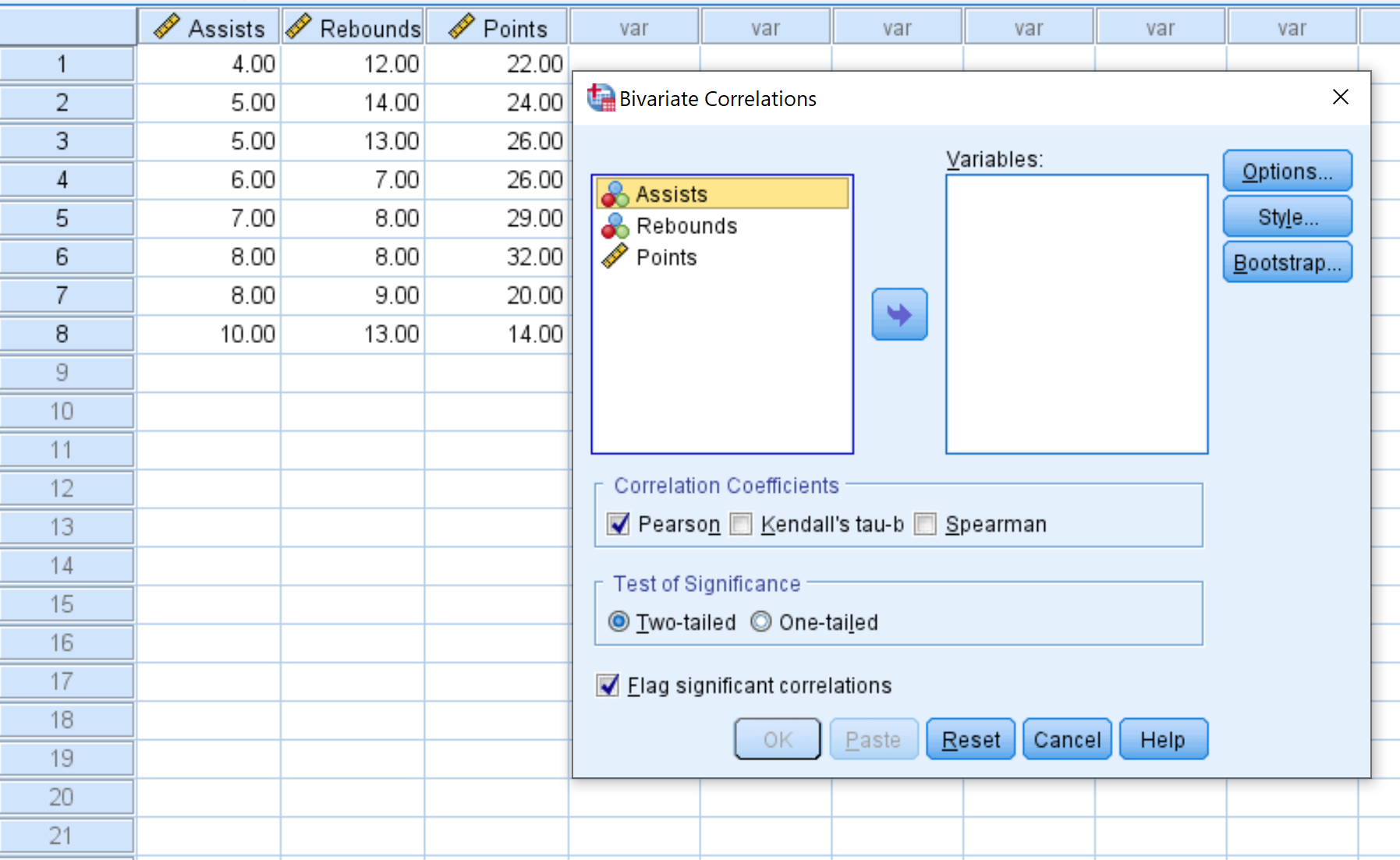
Langkah 2: Buat matriks korelasi.

Setiap variabel dalam dataset awalnya akan ditampilkan di kotak sebelah kiri:

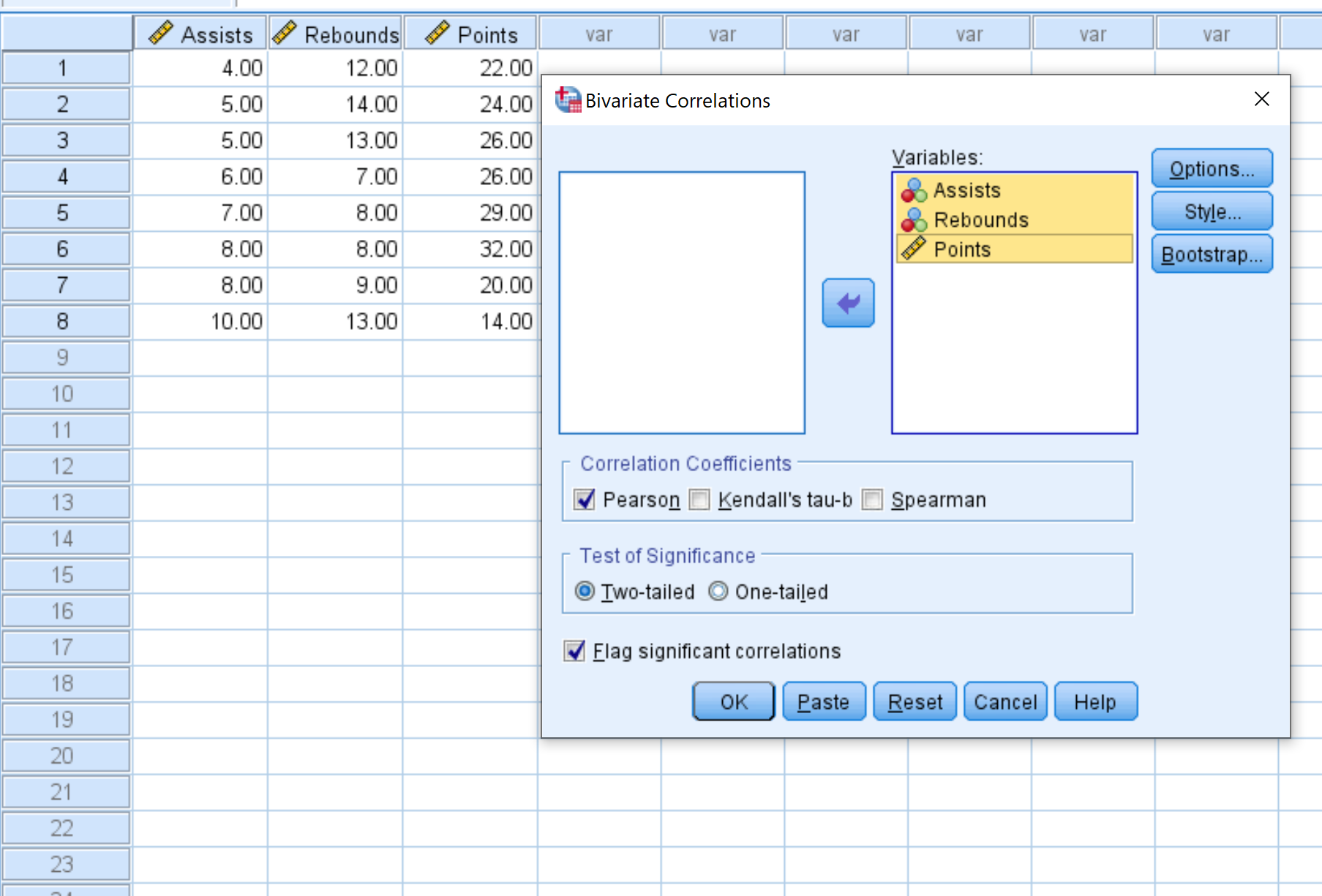
• Pilih setiap variabel yang ingin Anda sertakan dalam matriks korelasi dan klik panah untuk memindahkannya ke kotak Variabel . Kami akan menggunakan ketiga variabel dalam contoh ini.
• Di bawah Koefisien Korelasi , pilih apakah Anda ingin menggunakan korelasi Pearson, tau Kendall, atau korelasi Spearman. Kami akan membiarkannya sebagai Pearson untuk contoh ini.
• Di bawah Uji Signifikansi , pilih apakah Anda ingin menggunakan uji dua sisi atau satu sisi untuk menentukan apakah dua variabel memiliki hubungan yang signifikan secara statistik. Kami akan membiarkannya sebagai dua sisi.
• Centang kotak di samping Laporkan korelasi signifikan jika Anda ingin SPSS melaporkan variabel yang berkorelasi signifikan.
• Terakhir, klik OK .

Setelah Anda mengklik OK , matriks korelasi berikut akan muncul:

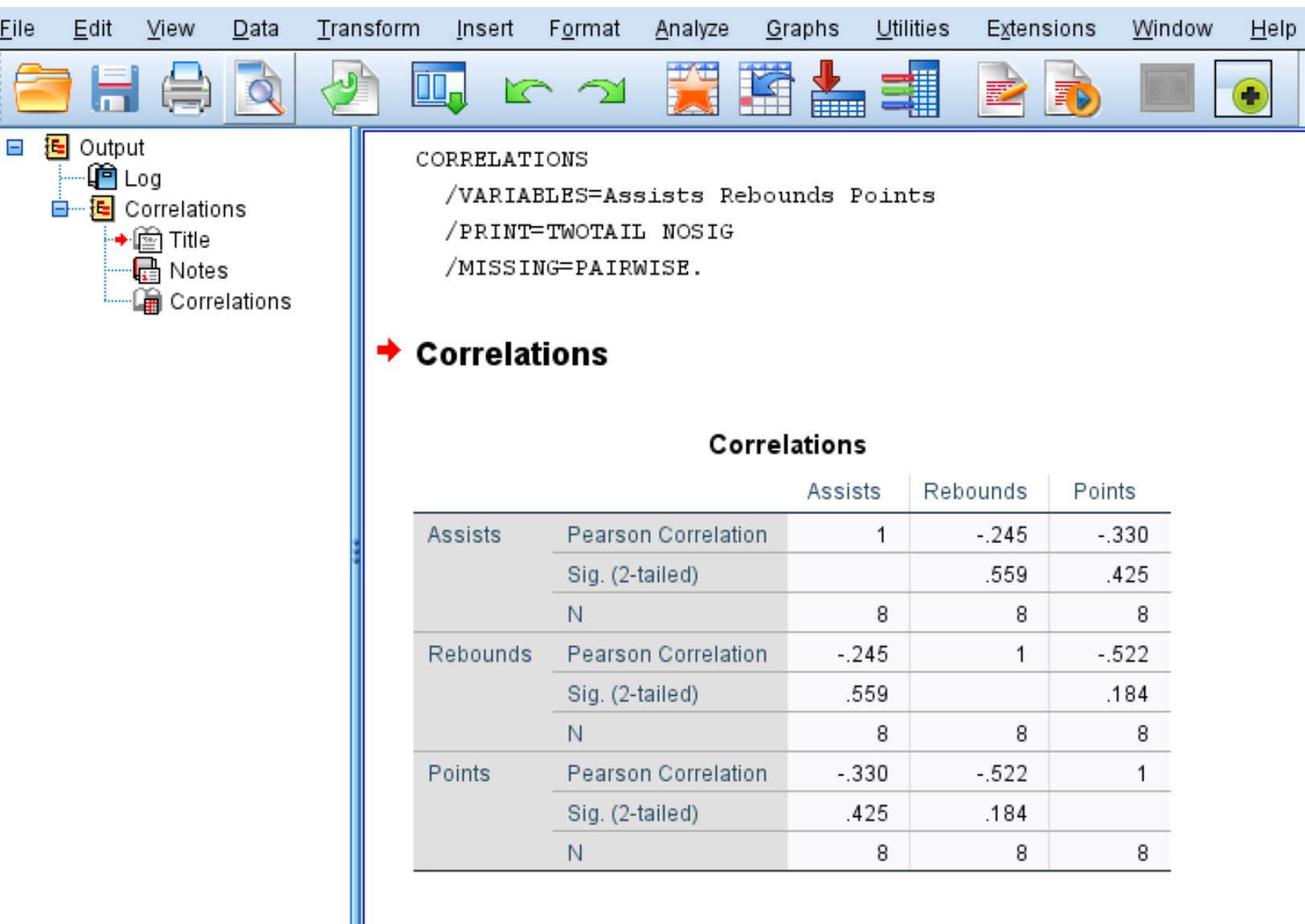
Langkah 3: Interpretasikan matriks korelasi.

Matriks korelasi menampilkan tiga pengukuran berikut untuk setiap variabel:

• Korelasi Pearson: ukuran hubungan linier antara dua variabel, berkisar antara -1 hingga 1.
• tanda tangan. (dua sisi): nilai p dua sisi yang terkait dengan koefisien korelasi. Ini memberitahu Anda jika dua variabel memiliki hubungan yang signifikan secara statistik (misalnya jika p <0,05)
• N : jumlah pasangan yang digunakan untuk menghitung koefisien korelasi Pearson.

Misalnya, berikut cara menginterpretasikan hasil variabel Assists:

• Koefisien korelasi Pearson antara assist dan rebound adalah -0,245 . Karena angka ini negatif, berarti kedua variabel tersebut mempunyai hubungan negatif.
• Nilai p yang terkait dengan koefisien korelasi Pearson untuk assist dan rebound adalah 0,559 . Karena nilai ini tidak kurang dari 0,05, kedua variabel tersebut tidak mempunyai hubungan yang signifikan secara statistik.
• Jumlah pasangan yang digunakan untuk menghitung koefisien korelasi Pearson adalah 8 (misalnya, 8 pasang pemain digunakan dalam perhitungan ini).

Langkah 4: Visualisasikan matriks korelasi.

Anda juga dapat membuat matriks plot sebar untuk memvisualisasikan hubungan linier antara masing-masing variabel.

• Klik tab Bagan .
• Klik Pembuat Bagan .

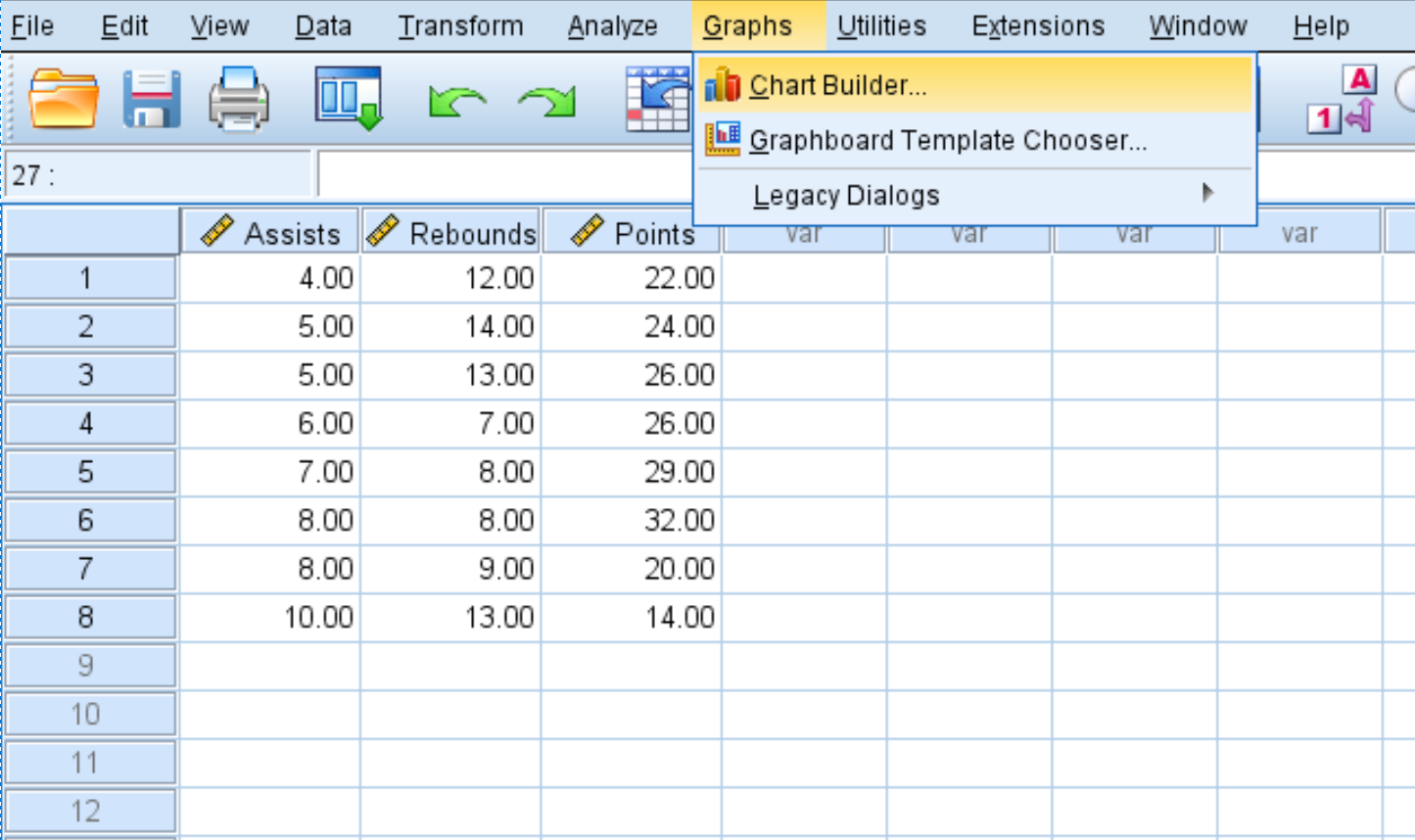
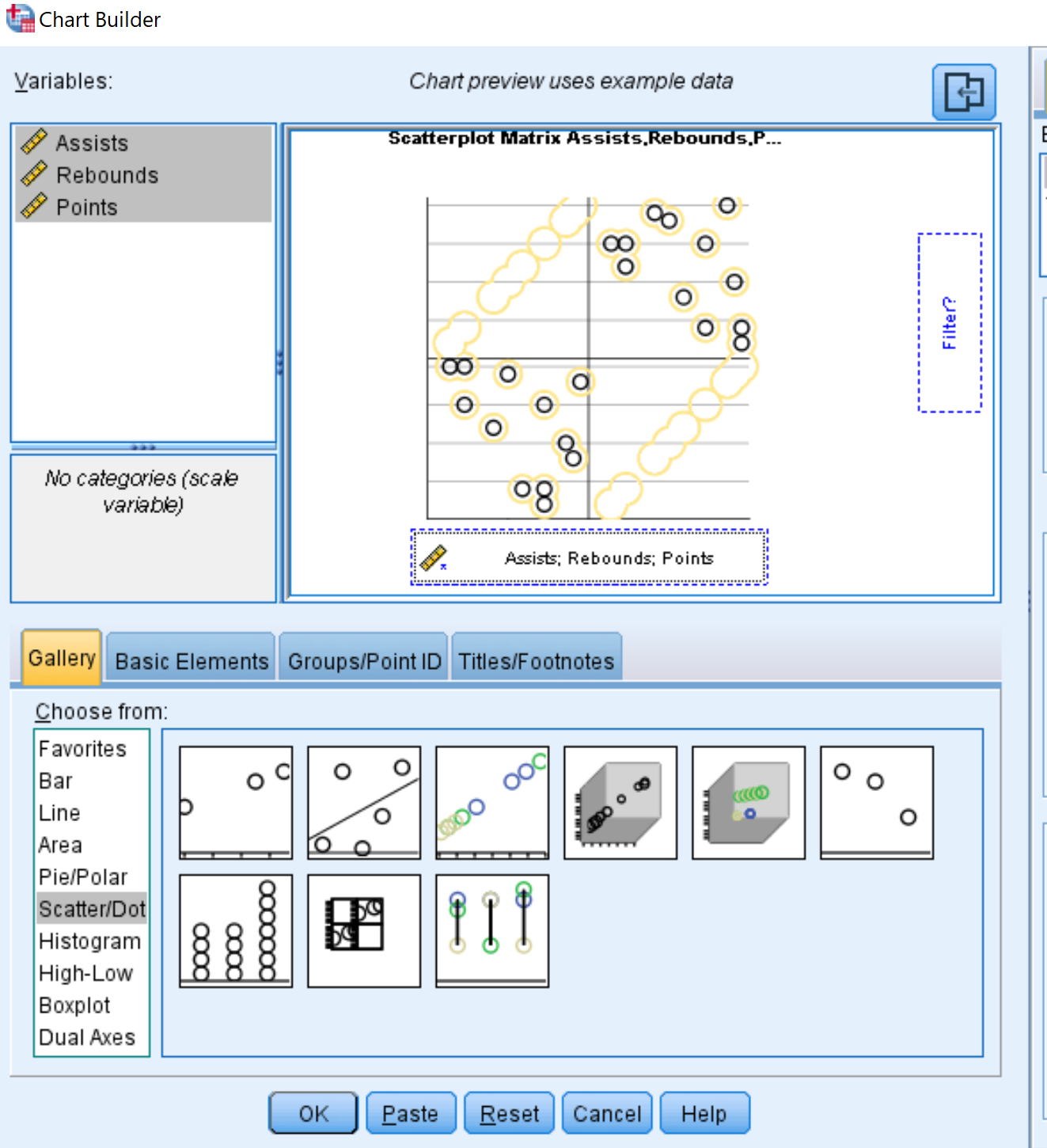
• Untuk tipe bagan, klik Sebar/Titik .
• Klik pada gambar yang bertuliskan Scatterplot Matrix .
• Di kotak Variabel di kiri atas, tahan Ctrl dan klik tiga nama variabel. Seret mereka ke kotak di bagian bawah bagan yang bertuliskan Scattermatrix .
• Terakhir, klik OK .

Matriks scatterplot berikut akan otomatis muncul:

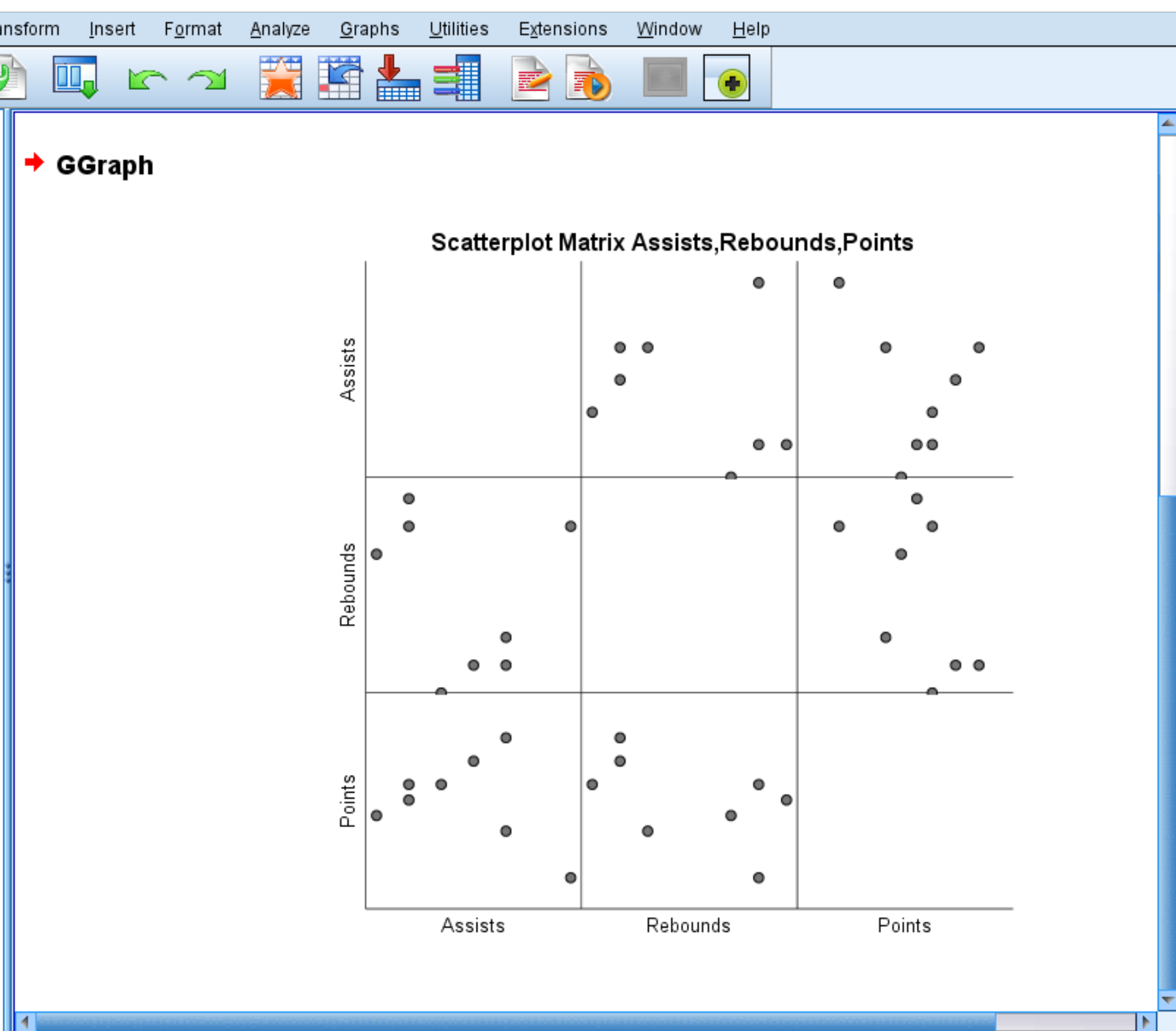
Setiap diagram sebar individu menunjukkan kombinasi berpasangan antara dua variabel. Misalnya, plot pencar di sudut kiri bawah menunjukkan kombinasi poin dan assist berpasangan untuk masing-masing dari 8 pemain dalam kumpulan data.

Matriks scatterplot bersifat opsional, tetapi ini memberikan cara yang baik untuk memvisualisasikan hubungan antara setiap kombinasi variabel berpasangan dalam kumpulan data.