Cara mencari median data yang dikelompokkan: dengan contoh

Kita sering kali ingin menghitung median data yang dikelompokkan bersama dengan cara tertentu.

Ingatlah bahwa median mewakili nilai yang terletak tepat di tengah kumpulan data, ketika semua nilai diurutkan dari terkecil hingga terbesar.

Misalnya, kita memiliki data yang dikelompokkan berikut:

Meskipun tidak mungkin menghitung median secara pasti karena kita tidak mengetahui nilai data mentahnya , median dapat diperkirakan dengan menggunakan rumus berikut:

Median data yang dikelompokkan = L + W[(N/2 – C) / F]

Emas:

• L : Batas bawah kelas median
• W : Median lebar kelas
• N : Frekuensi total
• C : Frekuensi kumulatif sampai dengan median kelas
• F : Median frekuensi kelas

Catatan : Kelas menengah adalah kelas yang memuat nilai yang terletak di N/2. Pada contoh di atas, terdapat N = 23 nilai total. Jadi nilai mediannya adalah pada posisi 23/2 = 11,5 yaitu pada kelas 21-30.

Contoh berikut menunjukkan cara menghitung median data yang dikelompokkan dalam berbagai skenario.

Contoh 1: Hitung Median Data yang Dikelompokkan

Misalkan kita mempunyai distribusi frekuensi berikut yang menunjukkan ujian yang dinilai oleh 40 siswa di kelas tertentu:

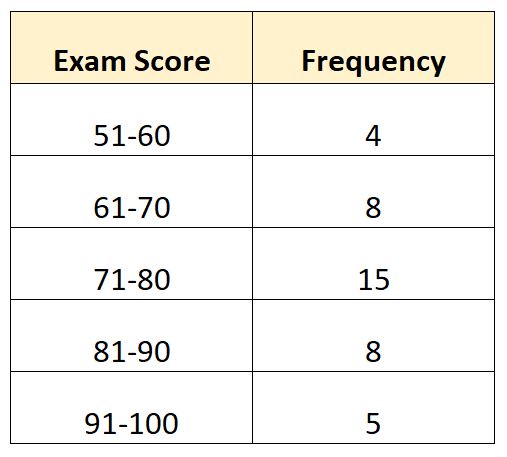
Dalam contoh ini, ada N = 40 nilai total. Jadi nilai mediannya ada pada kelas yang letaknya 40/2 = 20. Nilai terbesar ke-20 berada di kelas 71-80 .

Mengetahui hal ini, kita dapat menghitung nilai berikut:

• L : Batas kelas menengah bawah: 71
• W : Median lebar kelas: 9
• N : Total frekuensi: 40
• C : Frekuensi kumulatif sampai dengan kelas median: 12
• F : Median frekuensi kelas: 15

Kita dapat memasukkan nilai-nilai ini ke dalam rumus untuk menghitung median distribusi:

• Median = L + W[(N/2 – C) / F]
• Median = 71 + 9[(40/2 – 12) / 15]
• Median = 75,8

Kami memperkirakan nilai median ujian adalah 75,8 .

Contoh 2: Hitung Median Data yang Dikelompokkan

Misalkan kita mempunyai distribusi frekuensi berikut yang menunjukkan jumlah poin yang dicetak per pertandingan oleh 60 pemain bola basket:

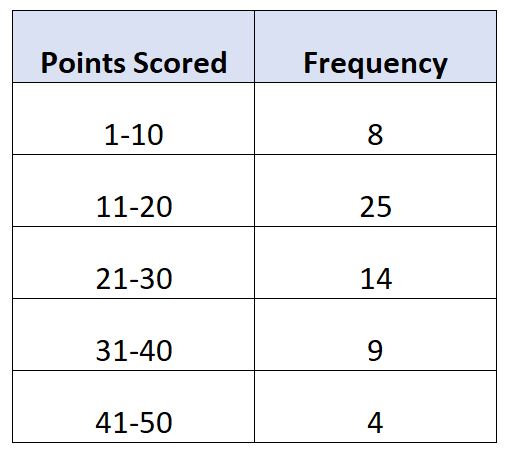
Dalam contoh ini, ada N = 60 nilai total. Jadi, nilai mediannya berada pada kelas dimana 60/2 = 30 berada. Nilai terbesar ke-30 berada di kelas 11-20 .

Mengetahui hal ini, kita dapat menghitung nilai berikut:

• L : Batas kelas menengah ke bawah: 11
• W : Median lebar kelas: 9
• N : Total frekuensi: 60
• C : Frekuensi kumulatif sampai dengan median kelas : 8
• F : Median frekuensi kelas: 25

Kita dapat memasukkan nilai-nilai ini ke dalam rumus untuk menghitung median distribusi:

• Median = L + W[(N/2 – C) / F]
• Median = 11 + 9[(60/2 – 8) / 25]
• Median = 18,92

Kami memperkirakan nilai median ujian adalah 18,92 .

Sumber daya tambahan

Tutorial berikut menjelaskan cara melakukan operasi umum lainnya dengan data yang dikelompokkan:

Cara mencari mean dan deviasi standar data yang dikelompokkan
Cara menemukan mode data berkelompok
Cara menghitung peringkat persentil untuk data yang dikelompokkan