Panduan lengkap: cara menafsirkan hasil anova di excel

ANOVA satu arah digunakan untuk menentukan apakah terdapat perbedaan yang signifikan secara statistik antara rata-rata tiga atau lebih kelompok independen.

Contoh berikut memberikan panduan lengkap tentang cara menginterpretasikan hasil ANOVA satu arah di Excel.

Contoh: Cara menginterpretasikan hasil ANOVA di Excel

Misalkan seorang guru secara acak meminta 30 siswa di kelasnya untuk menggunakan salah satu dari tiga metode belajar untuk mempersiapkan ujian.

Tangkapan layar berikut menunjukkan skor siswa berdasarkan metode yang mereka gunakan:

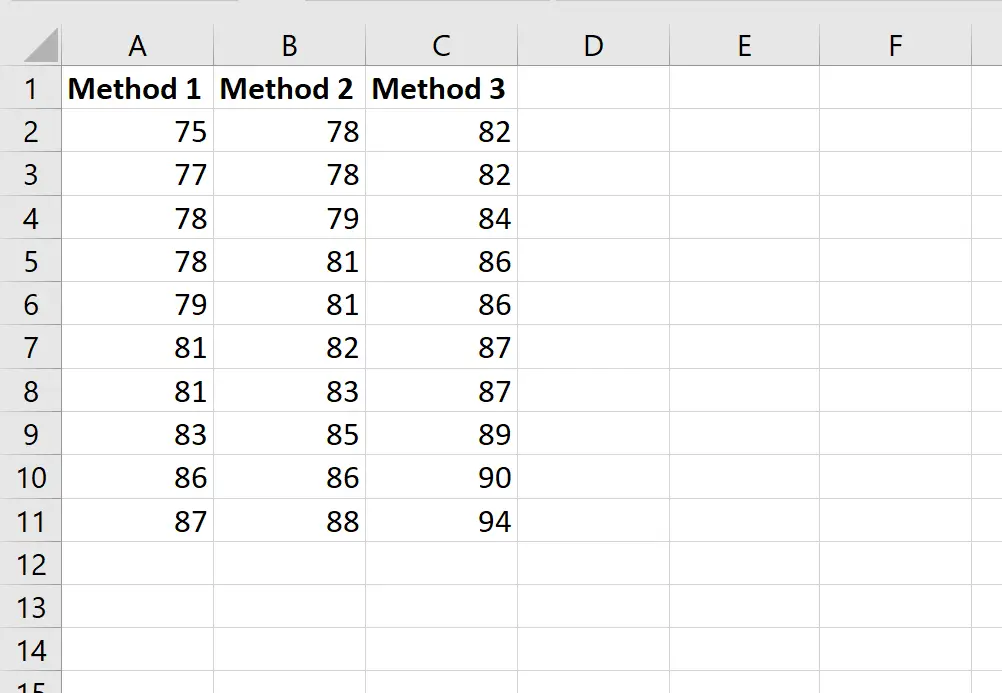
Misalkan guru ingin melakukan ANOVA satu arah untuk menentukan apakah skor rata-rata ketiga kelompok sama.

Untuk melakukan ANOVA satu arah di Excel, klik tab Data di sepanjang pita atas, lalu klik Analisis Data di grup Analisis .

Jika Anda tidak melihat opsi Analisis Data , Anda harus memuat perangkat lunak Analysis ToolPak gratis terlebih dahulu.

Setelah Anda mengkliknya, jendela baru akan muncul. Pilih Anova: Faktor Tunggal , lalu klik OK .

Di jendela baru yang muncul, masukkan informasi berikut:

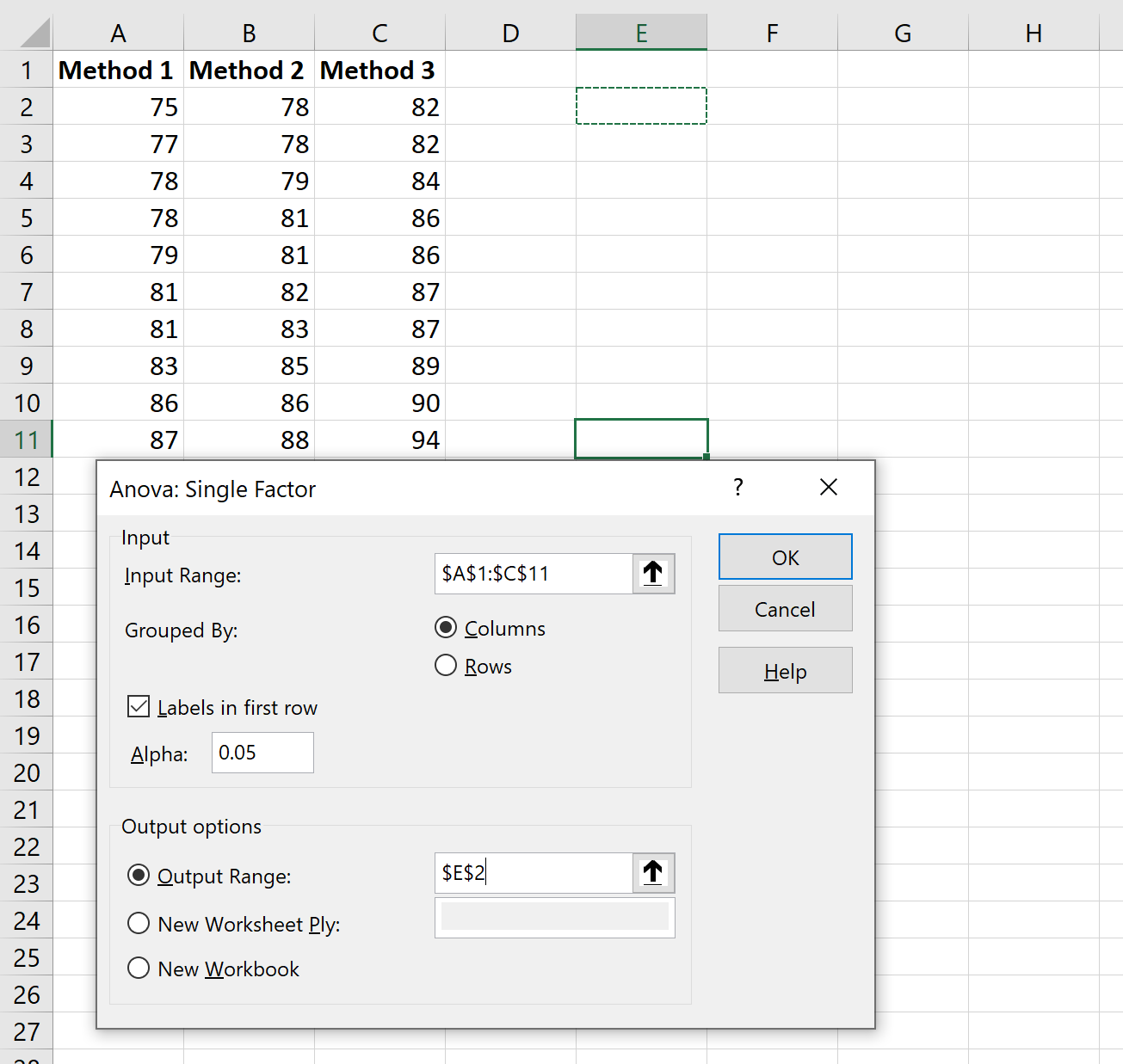
Setelah Anda mengklik OK , maka akan muncul hasil ANOVA satu arah:

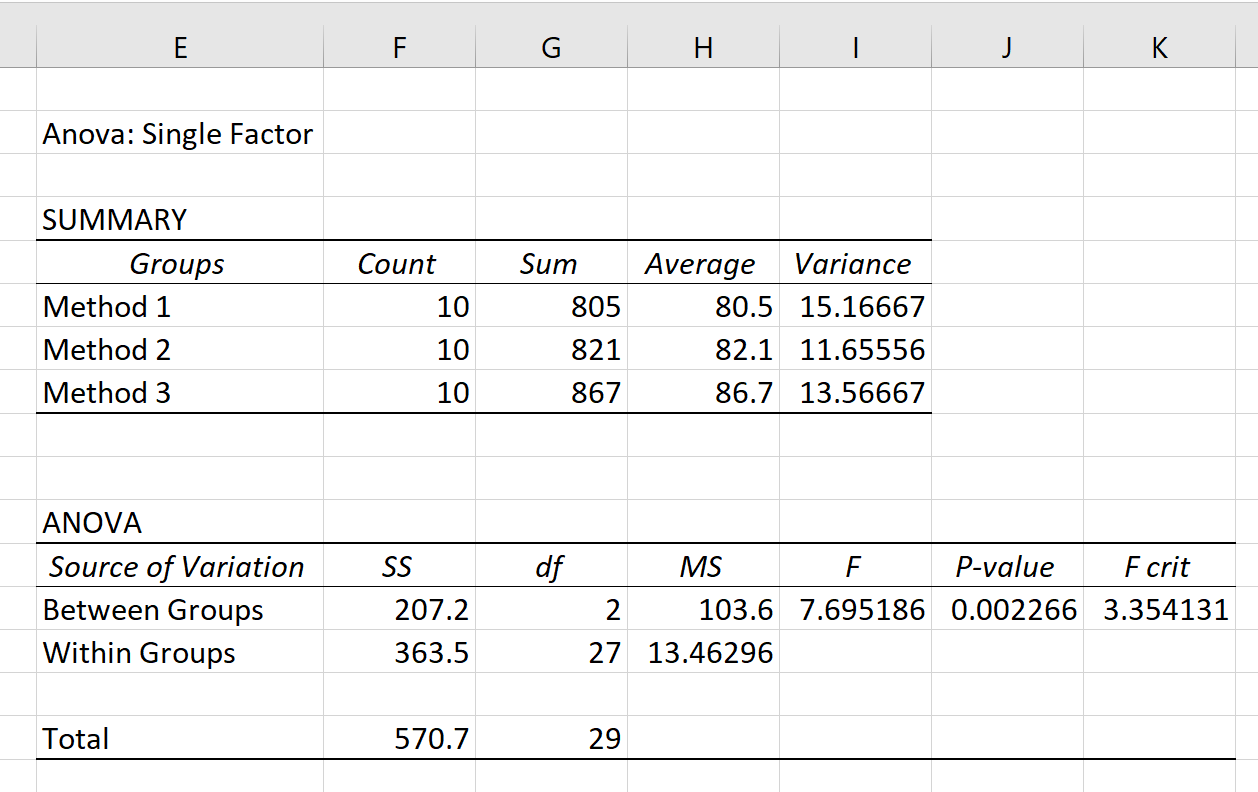
Dua tabel ditampilkan dalam hasilnya: SUMMARY dan ANOVA .

Berikut cara menginterpretasikan nilai pada setiap tabel:

Tabel RINGKASAN :

• Grup : Nama grup
• Count : Banyaknya observasi pada masing-masing kelompok
• Sum : Jumlah nilai masing-masing kelompok
• Rata-rata : Nilai rata-rata pada setiap kelompok
• Varians : Varians nilai pada setiap kelompok

Tabel ini memberi kita beberapa ringkasan statistik yang berguna untuk setiap kelompok yang digunakan dalam ANOVA.

Dari tabel ini kita dapat melihat bahwa siswa yang menggunakan Metode 3 memiliki rata-rata nilai ujian tertinggi (86,7), namun mereka juga memiliki varian nilai ujian tertinggi. ulasan (13.56667).

Untuk menentukan apakah perbedaan rata-rata kelompok signifikan secara statistik, kita harus mengacu pada tabel ANOVA.

Tabel ANOVA :

• Sumber variasi : variasi yang diukur (baik antar kelompok atau dalam kelompok)
• SS : Jumlah kuadrat untuk setiap sumber variasi
• df : Derajat kebebasan, dihitung sebagai #groups-1 untuk df Between dan #observations – #groups untuk df Within
• MS : Jumlah rata-rata kuadrat, dihitung dalam SS/df
• F : Nilai F keseluruhan, dihitung sebagai MS Between / MS Within
• Nilai-P : Nilai-p yang sesuai dengan nilai-F keseluruhan
• F crit : Nilai kritis F yang sesuai dengan α = 0,05

Nilai terpenting dalam tabel ini adalah p-value , yang ternyata adalah 0.002266 .

Ingatlah bahwa ANOVA satu arah menggunakan hipotesis nol dan hipotesis alternatif berikut:

• H ₀ : Semua mean grup adalah sama.
• H _A : Tidak semua rata-rata kelompok sama.

Karena nilai p kurang dari α = 0,05, kami menolak hipotesis nol ANOVA satu arah dan menyimpulkan bahwa kami memiliki cukup bukti untuk menyatakan bahwa semua mean kelompok tidak sama.

Artinya, tidak ketiga metode belajar tersebut menghasilkan rata-rata nilai ujian yang sama.

Catatan : Anda juga dapat membandingkan nilai F keseluruhan dengan nilai F kritis untuk menentukan apakah Anda harus menolak hipotesis nol atau tidak. Dalam hal ini, karena nilai keseluruhan F lebih besar dari nilai kritis F, hipotesis nol akan ditolak. Perhatikan bahwa pendekatan nilai-p dan pendekatan nilai-F kritis akan selalu menghasilkan kesimpulan yang sama.

Sumber daya tambahan

Tutorial berikut menjelaskan cara melakukan ANOVA yang berbeda di Excel:

Bagaimana Melakukan ANOVA Satu Arah di Excel
Cara Melakukan ANOVA Dua Arah di Excel
Cara Melakukan ANOVA Pengukuran Berulang di Excel
Cara Melakukan Nested ANOVA di Excel