Bagaimana menafsirkan rasio odds

Dalam statistik, probabilitas mengacu pada peluang terjadinya suatu peristiwa. Ini dihitung sebagai berikut:

KEMUNGKINAN:

P(peristiwa) = (# hasil yang diinginkan) / (# kemungkinan hasil)

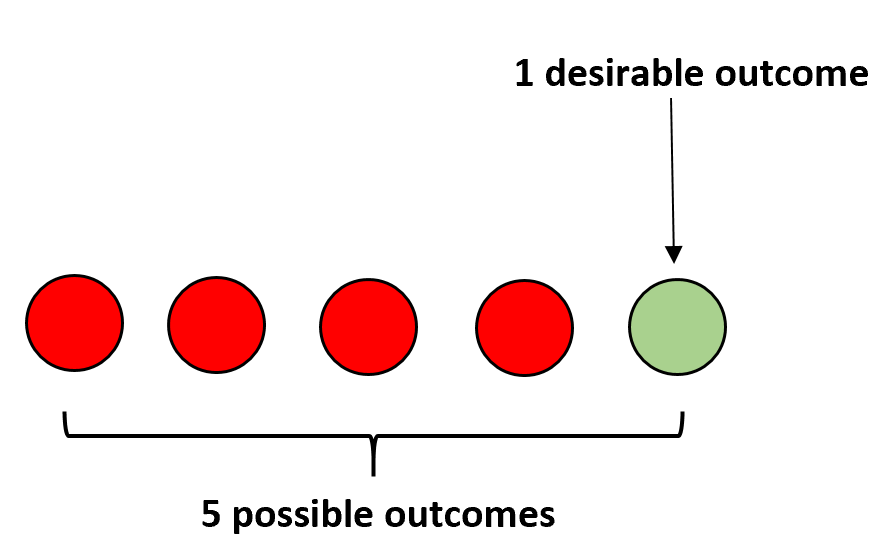
Misalnya, kita mempunyai empat bola merah dan satu bola hijau di dalam tas. Jika Anda menutup mata dan memilih sebuah bola secara acak, peluang terambilnya bola hijau dihitung sebagai berikut:

P(hijau) = 1 / 5 = 0,2 .

Peluang terjadinya suatu peristiwa dapat dihitung sebagai berikut:

KEMUNGKINAN:

Peluang (peristiwa) = P (peristiwa terjadi) / 1-P (peristiwa terjadi)

Misalnya, peluang menembak bola hijau adalah (0.2)/1-(0.2) = 0.2/0.8 = 0.25 .

Rasio odds adalah rasio dua probabilitas.

LAPORAN KEBERUNTUNGAN:

Rasio Odds = Peluang Event A / Peluang Event B

Misalnya kita bisa menghitung odds rasio antara memilih bola merah dan bola hijau.

Peluang terambilnya bola merah adalah 4/5 = 0,8 .

Peluang terambilnya bola merah adalah (0.8) / 1-(0.8) = 0.8 / 0.2 = 4 .

Rasio odds pemilihan bola merah dibandingkan bola hijau dihitung sebagai berikut:

Peluang (merah) / Peluang (hijau) = 4 / 0,25 = 16 .

Jadi peluang tertembaknya bola merah 16 kali lebih besar dibandingkan peluang tertembaknya bola hijau.

Kapan rasio odds digunakan di dunia nyata?

Di dunia nyata, rasio odds digunakan dalam berbagai konteks di mana peneliti ingin membandingkan peluang terjadinya dua peristiwa. Berikut beberapa contohnya.

Contoh #1: Menafsirkan rasio odds

Para peneliti ingin mengetahui apakah pengobatan baru meningkatkan kemungkinan pasien mendapatkan hasil kesehatan yang positif dibandingkan dengan pengobatan yang sudah ada. Tabel berikut menunjukkan jumlah pasien yang mengalami hasil kesehatan positif atau negatif, bergantung pada pengobatannya.

Peluang pasien mendapatkan hasil positif dengan pengobatan baru dapat dihitung sebagai berikut:

Peluang = P(positif) / 1 – P(positif) = (50/90) / 1-(50/90) = (50/90) / (40/90) = 1,25

Peluang pasien mendapatkan hasil positif dengan pengobatan yang ada dapat dihitung sebagai berikut:

Peluang = P(positif) / 1 – P(positif) = (42/90) / 1-(42/90) = (42/90) / (48/90) = 0,875

Dengan demikian, rasio odds untuk mencapai hasil positif dengan pengobatan baru dibandingkan dengan pengobatan yang ada dapat dihitung sebagai berikut:

Rasio peluang = 1,25 / 0,875 = 1,428 .

Kami menafsirkan hal ini berarti bahwa peluang pasien mendapatkan hasil positif dengan menggunakan pengobatan baru adalah 1,428 kali lipat peluang pasien mendapatkan hasil positif dengan menggunakan pengobatan yang ada.

Dengan kata lain, kemungkinan mendapatkan hasil positif meningkat sebesar 42,8% dengan pengobatan baru.

Contoh #2: Menafsirkan rasio odds

Pemasar ingin mengetahui apakah sebuah iklan membuat pelanggan membeli suatu barang lebih sering dibandingkan iklan lainnya. Jadi mereka menampilkan setiap iklan kepada 100 orang. Tabel berikut menunjukkan jumlah orang yang membeli item berdasarkan iklan yang mereka lihat:

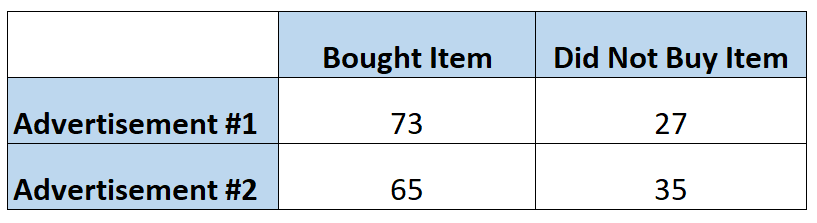
Peluang seseorang membeli barang tersebut setelah melihat iklan pertama dapat dihitung sebagai berikut:

Peluang = P(dibeli) / 1 – P(dibeli) = (73/100) / 1-(73/100) = (73/100) / (27/100) = 2,704

Peluang seseorang membeli barang tersebut setelah melihat iklan kedua dapat dihitung sebagai berikut:

Peluang = P(dibeli) / 1 – P(dibeli) = (65/100) / 1-(65/10) = (65/100) / (35/100) = 1,857

Jadi rasio peluang pelanggan yang membeli barang setelah melihat iklan pertama versus membeli setelah melihat iklan kedua dapat dihitung sebagai berikut:

Rasio peluang = 2,704 / 1,857 = 1,456 .

Kami menafsirkan hal ini berarti bahwa peluang seseorang membeli barang tersebut setelah melihat iklan pertama adalah 1,456 kali peluang seseorang membeli barang tersebut setelah melihat iklan kedua.

Dengan kata lain, peluang membeli item tersebut meningkat sebesar 45,6% berkat listing pertama.

Sumber daya tambahan

Cara Menghitung Rasio Odds dan Risiko Relatif di Excel
Bagaimana menafsirkan rasio odds kurang dari 1
Bagaimana menafsirkan risiko relatif