Mengapa deviasi standar penting? (penjelasan + contoh)

Standar deviasi digunakan untuk mengukur sebaran nilai dalam suatu sampel.

Kita dapat menggunakan rumus berikut untuk menghitung deviasi standar sampel tertentu:

√ Σ( _xi – x _batang ) ² / (n-1)

Emas:

• Σ: Simbol yang berarti “jumlah”
• x _i : nilai ^ke-i dari sampel
• x _bar : Arti sampel
• n: Ukuran sampel

Semakin tinggi nilai standar deviasi, maka semakin tersebar nilai-nilai tersebut dalam suatu sampel. Sebaliknya, semakin rendah nilai standar deviasinya, maka semakin erat pengelompokannya.

Pertanyaan yang sering diajukan siswa adalah: Mengapa standar deviasi itu penting?

Jawabannya: Standar deviasi penting karena memberitahu kita distribusi nilai dalam kumpulan data tertentu.

kami menganalisis kumpulan data Kapan pun, kami ingin menemukan metrik berikut:

• Pusat kumpulan data . Cara paling umum untuk mengukur “pusat” adalah dengan menggunakan mean dan median.
• Distribusi nilai dalam dataset . Cara paling umum untuk mengukur penyebaran adalah dengan menggunakan standar deviasi.

Dengan mengetahui dimana letak pusatnya dan bagaimana sebaran nilainya, maka kita dapat memahami dengan baik sebaran nilai pada suatu kumpulan data.

Contoh berikut menggambarkan pentingnya deviasi standar dalam praktik.

Contoh 1: Pembagian gaji

Asumsikan gaji rata-rata di perusahaan A adalah $80.000 dan deviasi standarnya adalah $20.000. Karena standar deviasinya sangat besar, tidak ada jaminan bahwa Anda akan dibayar mendekati $80.000 per tahun jika Anda bekerja di perusahaan ini karena ada variasi gaji yang begitu besar.

Sebaliknya, misalkan gaji rata-rata di Perusahaan B juga $80.000, namun deviasi standarnya hanya $4.000. Karena deviasi standar ini sangat kecil, Anda dapat yakin bahwa Anda akan dibayar mendekati $80.000 karena variasi gajinya sangat kecil.

Jika kita membuat boxplot untuk memvisualisasikan distribusi gaji di kedua perusahaan tersebut, maka tampilannya akan seperti ini:

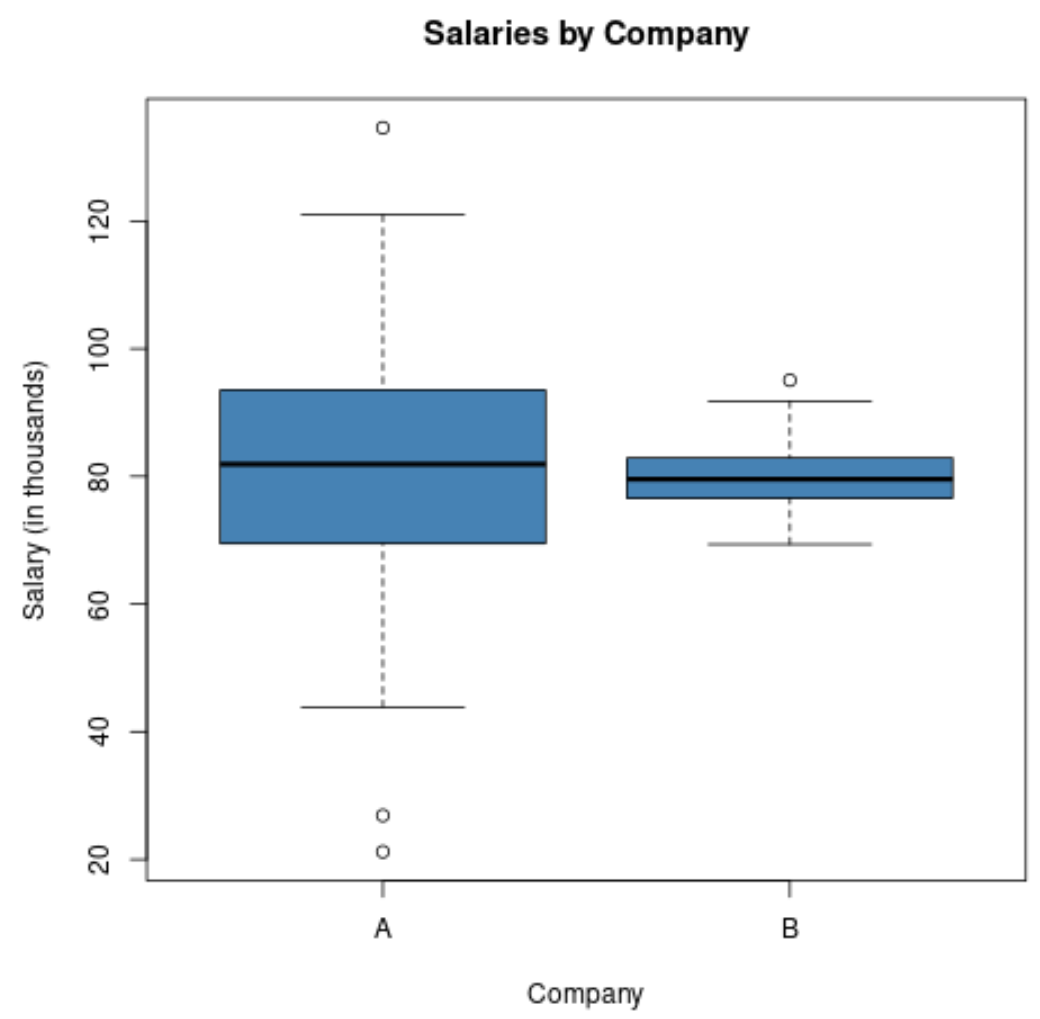
Perhatikan bahwa panjang plot kotak untuk perusahaan A lebih besar karena deviasi standar upah jauh lebih tinggi.

Kedua perusahaan memiliki gaji rata-rata yang sama, namun kesenjangan gaji jauh lebih tinggi di perusahaan A.

Contoh 2: Distribusi harga rumah

Asumsikan harga rata-rata rumah di lingkungan A adalah $250.000 dan deviasi standarnya adalah $50.000. Karena deviasi standarnya cukup besar, ini berarti beberapa harga rumah akan jauh lebih tinggi dari $250.000 dan yang lainnya akan jauh lebih rendah. Jika Anda melihat rumah mana pun di lingkungan ini, tidak ada jaminan bahwa harganya akan mendekati rata-rata.

Sebaliknya, misalkan harga rata-rata rumah di lingkungan B juga $250.000, namun deviasi standarnya hanya $10.000. Karena deviasi standar ini cukup kecil, Anda dapat yakin bahwa rumah mana pun yang Anda lihat di lingkungan tersebut kemungkinan besar akan mendekati harga ini.

Jika kita membuat diagram kotak untuk memvisualisasikan sebaran harga rumah di kedua lingkungan tersebut, maka tampilannya akan seperti ini:

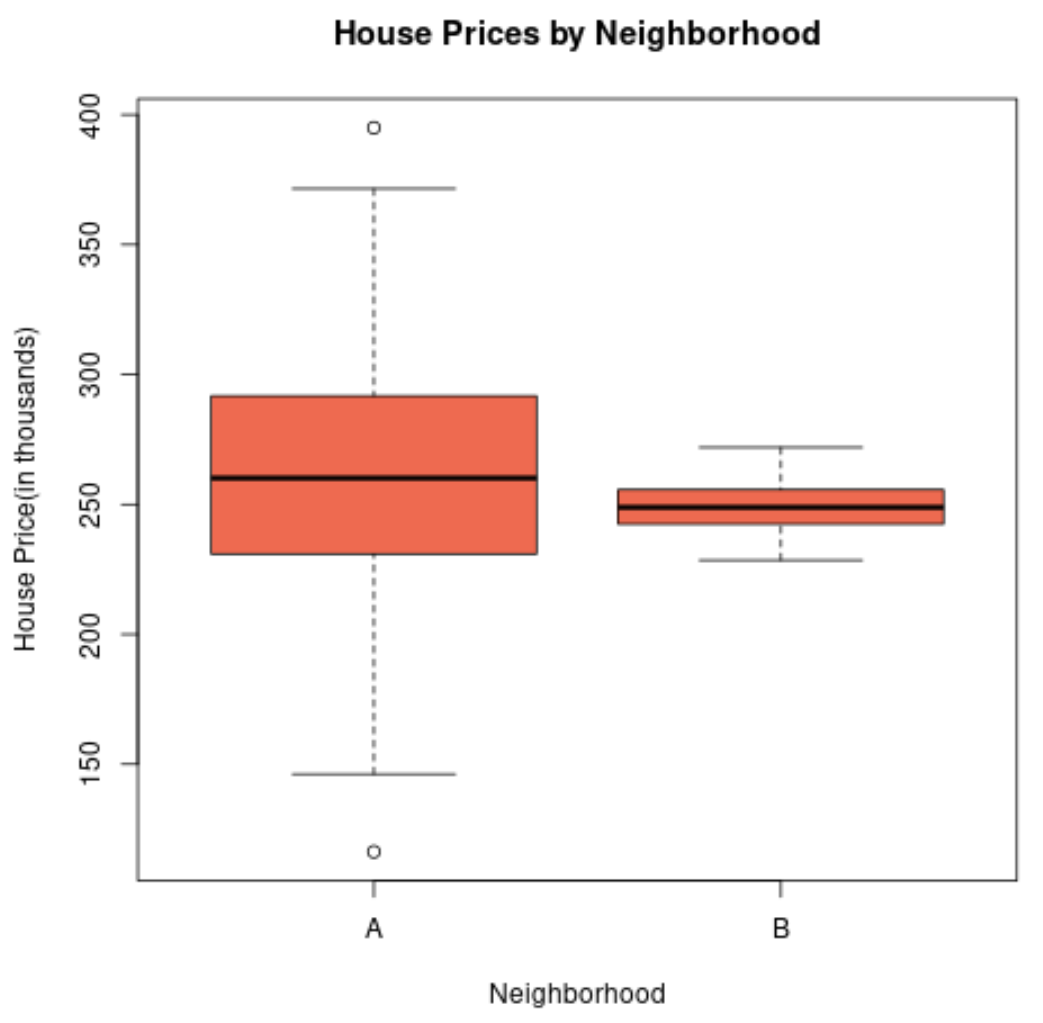
Panjang plot kotak lingkungan A lebih besar karena deviasi standar harga real estat jauh lebih tinggi.

Faktanya, harga rumah berkisar antara kurang dari $150.000 hingga lebih dari $400.000 untuk lingkungan A, sedangkan harga hanya berkisar antara $230.000 hingga $270.000 untuk lingkungan B.

Hanya dengan mengetahui deviasi standar harga rumah di setiap lingkungan, kita dapat mengetahui seberapa besar variasi harga yang diharapkan di setiap lingkungan.

Sumber daya tambahan

Apa yang dianggap sebagai deviasi standar yang baik?
Rentang vs. Deviasi Standar: Kapan Menggunakan Masing-masing
Koefisien variasi versus deviasi standar: perbedaan