Mengapa ukuran sampel penting? (penjelasan & contoh)
Ukuran sampel mengacu pada jumlah total orang yang terlibat dalam suatu eksperimen atau penelitian.
Ukuran sampel penting karena secara langsung mempengaruhi ketepatan estimasi parameter populasi.
Untuk memahami mengapa hal ini terjadi, ada baiknya jika kita memiliki pemahaman dasar tentang interval kepercayaan.
Penjelasan singkat tentang interval kepercayaan
Dalam statistik, kita sering kali berupaya mengukur parameter populasi – angka yang menggambarkan karakteristik tertentu dari keseluruhan populasi.
Misalnya, kita mungkin tertarik untuk mengukur tinggi rata-rata semua individu di kota tertentu.
Namun, pengumpulan data setiap individu dalam suatu populasi sering kali terlalu mahal dan memakan waktu. Jadi kita biasanya mengambil sampel acak dari populasi dan menggunakan data sampel untuk memperkirakan parameter populasi.
Misalnya, kita dapat mengumpulkan data tentang tinggi badan 100 individu secara acak di suatu kota. Kami kemudian dapat menghitung ukuran rata-rata individu dalam sampel. Namun, kita tidak dapat memastikan bahwa rata-rata sampel sama persis dengan rata-rata populasi.
Untuk memperhitungkan ketidakpastian ini, kita dapat membuat interval kepercayaan . Interval kepercayaan adalah rentang nilai yang kemungkinan memuat parameter populasi dengan tingkat kepercayaan tertentu.
Rumus untuk menghitung selang kepercayaan suatu mean populasi adalah:
Interval kepercayaan = x +/- z*(s/√ n )
Emas:
- x : mean sampel
- z : nilai z yang dipilih
- s: deviasi standar sampel
- n: ukuran sampel
Nilai z yang Anda gunakan bergantung pada tingkat kepercayaan yang Anda pilih. Tabel berikut menunjukkan nilai z yang sesuai dengan pilihan tingkat kepercayaan yang paling umum:
| Tingkat kepercayaan diri | nilai z |
|---|---|
| 0,90 | 1.645 |
| 0,95 | 1.96 |
| 0,99 | 2.58 |
Hubungan antara ukuran sampel dan interval kepercayaan
Misalkan kita ingin memperkirakan berat rata-rata suatu populasi penyu. Kami mengumpulkan sampel penyu secara acak dengan informasi berikut:
- Ukuran sampel n = 25
- Rata-rata berat sampel x = 300
- Simpangan baku sampel s = 18,5
Berikut cara menghitung interval kepercayaan 90% untuk bobot rata-rata populasi sebenarnya:
Interval kepercayaan 90%: 300 +/- 1,645*(18,5/√ 25 ) = [293,91, 306,09]
Kami yakin 90% bahwa rata-rata berat penyu dalam populasi adalah antara 293,91 dan 306,09 pon.
Sekarang misalkan kita tidak hanya mengumpulkan 25 ekor penyu, tapi kita mengumpulkan data sebanyak 50 ekor penyu.
Berikut cara menghitung interval kepercayaan 90% untuk bobot rata-rata populasi sebenarnya:
Interval kepercayaan 90%: 300 +/- 1,645*(18,5/√ 50 ) = [295,79, 304,30]
Perhatikan bahwa interval kepercayaan ini lebih sempit dibandingkan interval kepercayaan sebelumnya. Ini berarti perkiraan kami mengenai berat rata-rata populasi penyu yang sebenarnya lebih akurat.
Sekarang misalkan kita mengumpulkan data 100 penyu.
Berikut cara menghitung interval kepercayaan 90% untuk bobot rata-rata populasi sebenarnya:
Interval kepercayaan 90%: 300 +/- 1,645*(18,5/√ 100 ) = [296,96, 303,04]
Perhatikan bahwa interval kepercayaan ini bahkan lebih sempit dibandingkan interval kepercayaan sebelumnya.
Tabel berikut merangkum masing-masing lebar interval kepercayaan:
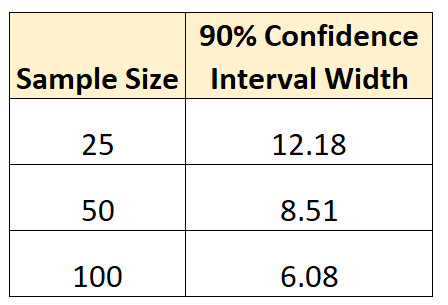
Intinya: Semakin besar ukuran sampel, semakin akurat kita dapat memperkirakan parameter populasi .
Sumber daya tambahan
Tutorial berikut memberikan penjelasan yang lebih bermanfaat tentang interval kepercayaan dan ukuran sampel.
Pengantar Interval Keyakinan
4 Contoh Confidence Interval dalam Kehidupan Nyata
Populasi vs. sampel: apa bedanya?