Cara mentransformasi data di r (log, akar kuadrat, akar kubus)

Banyak uji statistik yang mengasumsikan bahwa sisa variabel respons terdistribusi normal.

Namun, residu seringkali tidak terdistribusi secara normal. Salah satu cara untuk mengatasi masalah ini adalah dengan mentransformasikan variabel respon menggunakan salah satu dari tiga transformasi:

1. Transformasi log: ubah variabel respons dari y menjadi log(y) .

2. Transformasi akar kuadrat: Transformasikan variabel respon dari y menjadi √y .

3. Transformasi akar pangkat tiga: ubah variabel respon dari y menjadi y ^1/3 .

Dengan melakukan transformasi ini, variabel respon secara umum mendekati distribusi normal. Contoh berikut menunjukkan cara melakukan transformasi ini di R.

Transformasi log di R

Kode berikut menunjukkan cara melakukan transformasi log pada variabel respons:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform log transformation
log_y <- log10(df$y)

Kode berikut menunjukkan cara membuat histogram untuk menampilkan distribusi y sebelum dan sesudah melakukan transformasi log:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for log-transformed distribution 
hist(log_y, col='coral2', main='Log Transformed')

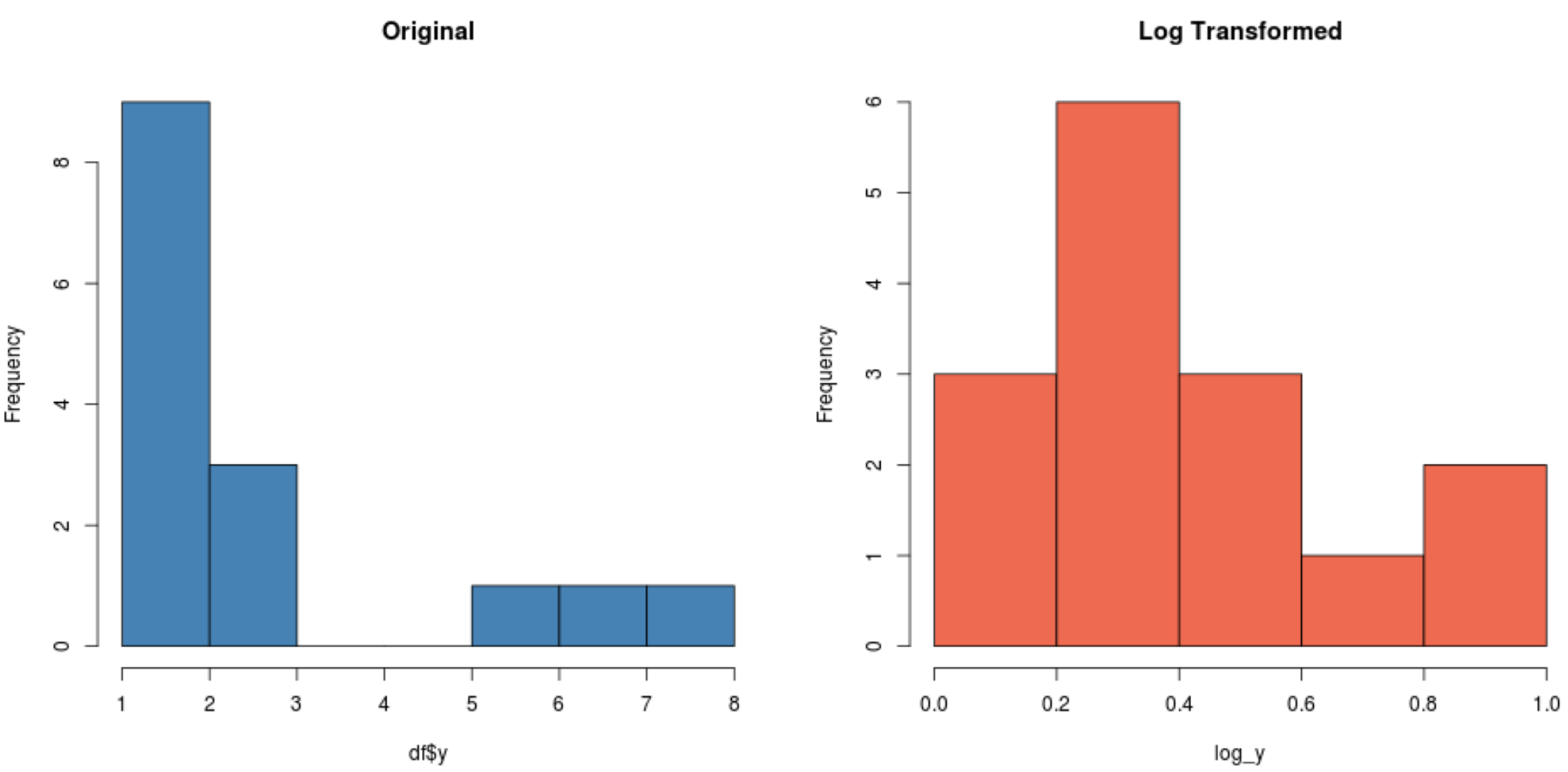
Perhatikan bagaimana distribusi transformasi log jauh lebih normal daripada distribusi aslinya. Ini masih bukan “bentuk lonceng” yang sempurna tetapi lebih mendekati distribusi normal daripada distribusi aslinya.

Faktanya, jika kita melakukan uji Shapiro-Wilk pada setiap distribusi, kita akan menemukan bahwa distribusi asli gagal memenuhi asumsi normalitas, sedangkan distribusi log-transformasi tidak (pada α = 0,05):

 #perform Shapiro-Wilk Test on original data
shapiro.test(df$y)

	Shapiro-Wilk normality test

data: df$y
W = 0.77225, p-value = 0.001655

#perform Shapiro-Wilk Test on log-transformed data 
shapiro.test(log_y)

	Shapiro-Wilk normality test

data:log_y
W = 0.89089, p-value = 0.06917

Transformasi akar kuadrat di R

Kode berikut menunjukkan cara melakukan transformasi akar kuadrat pada variabel respon:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform square root transformation
sqrt_y <- sqrt(df$y)

Kode berikut menunjukkan cara membuat histogram untuk menampilkan distribusi y sebelum dan sesudah melakukan transformasi akar kuadrat:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for square root-transformed distribution 
hist(sqrt_y, col='coral2', main='Square Root Transformed') 

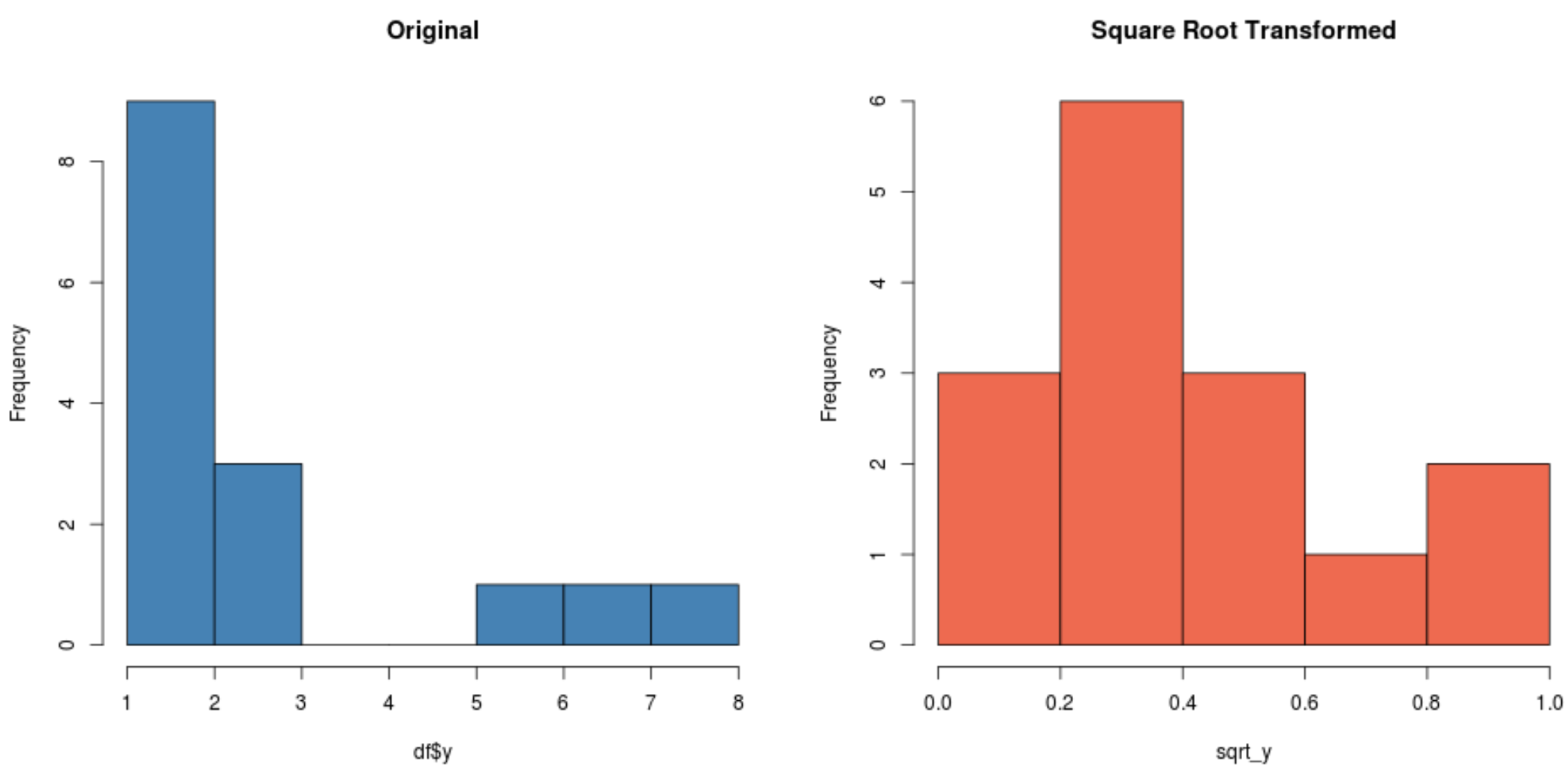
Perhatikan bagaimana distribusi transformasi akar kuadrat jauh lebih terdistribusi normal daripada distribusi aslinya.

Transformasi akar pangkat tiga di R

Kode berikut menunjukkan cara melakukan transformasi akar pangkat tiga pada variabel respon:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform square root transformation
cube_y <- df$y^(1/3)

Kode berikut menunjukkan cara membuat histogram untuk menampilkan distribusi y sebelum dan sesudah melakukan transformasi akar kuadrat:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for square root-transformed distribution 
hist(cube_y, col='coral2', main='Cube Root Transformed') 

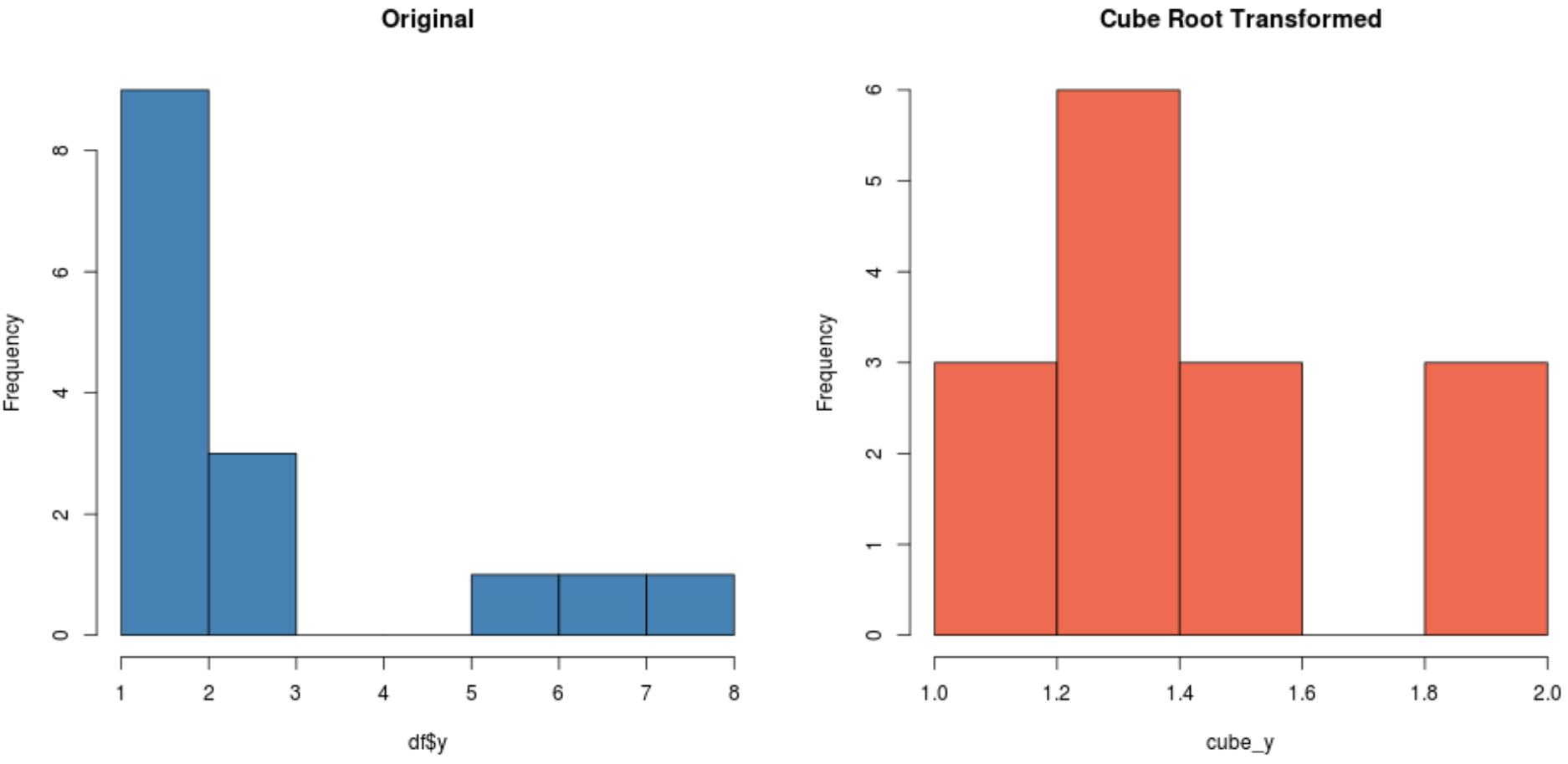
Bergantung pada kumpulan data Anda, salah satu transformasi ini mungkin menghasilkan kumpulan data baru yang terdistribusi lebih normal dibandingkan yang lain.