Ukuran tendensi sentral: pengertian & contoh
Ukuran tendensi sentral adalah nilai tunggal yang mewakili titik pusat suatu kumpulan data. Nilai ini juga bisa disebut “lokasi pusat” dari kumpulan data.
Dalam statistik, ada tiga ukuran tendensi sentral yang umum:
- Rata-rata
- median
- Mode
Masing-masing ukuran ini menemukan lokasi pusat kumpulan data menggunakan metode berbeda. Bergantung pada jenis data yang Anda analisis, mungkin lebih baik menggunakan salah satu dari tiga metrik ini dibandingkan dua metrik lainnya.
Dalam artikel ini, kita akan melihat cara menghitung masing-masing dari tiga ukuran tendensi sentral serta cara menentukan ukuran mana yang terbaik untuk digunakan berdasarkan data Anda.
Mengapa ukuran tendensi sentral bermanfaat?
Sebelum kita melihat cara menghitung mean, median, dan modus, ada baiknya kita memahami terlebih dahulu mengapa pengukuran ini benar-benar berguna.
Pertimbangkan skenario berikut:
Sepasang suami istri muda sedang mencoba memutuskan di mana akan membeli rumah pertama mereka di kota baru dan jumlah terbesar yang dapat mereka belanjakan adalah $150.000. Beberapa wilayah kota memiliki rumah mahal, beberapa memiliki rumah murah, dan beberapa memiliki rumah dengan harga menengah. Mereka ingin dengan mudah mempersempit pencarian mereka ke lingkungan tertentu yang sesuai dengan anggaran mereka.
Jika pasangan tersebut hanya melihat harga rumah keluarga tunggal di setiap lingkungan, mereka mungkin akan kesulitan menentukan lingkungan mana yang paling sesuai dengan anggaran mereka, karena mereka mungkin melihat sesuatu seperti ini:
Harga rumah Lingkungan A : $140,000, $190,000, $265,000, $115,000, $270,000, $240,000, $250,000, $180,000, $160,000, $200,000, $240,000, $280,000,…
Harga rumah lingkungan B : $140,000, $290,000, $155,000, $165,000, $280,000, $220,000, $155,000, $185,000, $160,000, $200,000, $190,000, $140,000, $145.00 0,…
Harga rumah lingkungan C : $140,000, $130,000, $165,000, $115,000, $170,000, $100,000, $150,000, $180,000, $190,000, $120,000, $110,000, $130,000, $120,00 0,…
Namun, jika mereka mengetahui harga rata-rata (misalnya ukuran tendensi sentral) rumah di setiap lingkungan, maka mereka dapat menyaring pencariannya lebih cepat karena mereka dapat lebih mudah mengidentifikasi lingkungan mana yang memiliki harga rumah yang sesuai dengan anggaran mereka:
Harga rata-rata sebuah rumah di lingkungan A: $220,000
Harga rata-rata sebuah rumah di lingkungan B : $190,000
Harga rata-rata sebuah rumah di lingkungan C : $140,000
Dengan mengetahui harga rata-rata rumah di setiap lingkungan, mereka dapat dengan cepat melihat bahwa Lingkungan C kemungkinan memiliki jumlah rumah terbanyak sesuai anggaran mereka.
Inilah manfaat menggunakan ukuran tendensi sentral: membantu Anda memahami nilai sentral dari suatu kumpulan data, yang cenderung menggambarkan di mana letak nilai data secara umum. Dalam contoh khusus ini, hal ini membantu pasangan muda memahami harga khas sebuah rumah di setiap lingkungan.
Kesimpulan: Ukuran tendensi sentral berguna karena memberikan kita nilai tunggal yang menggambarkan “pusat” kumpulan data. Ini membantu kita memahami kumpulan data jauh lebih cepat daripada hanya melihat semua nilai individual dalam kumpulan data.
Berarti
Ukuran tendensi sentral yang paling umum digunakan adalah mean . Untuk menghitung rata-rata suatu kumpulan data, cukup jumlahkan semua nilai individual dan bagi dengan jumlah total nilai.
Rata-rata = (jumlah semua nilai) / (jumlah total nilai)
Misalnya, kita memiliki kumpulan data berikut yang menunjukkan jumlah home run yang dilakukan oleh 10 pemain bisbol di tim yang sama selama satu musim:
| Pemain | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #sepuluh |
|---|---|---|---|---|---|---|---|---|---|---|
| Home run | 8 | 15 | 22 | 21 | 12 | 9 | 11 | 27 | 14 | 13 |
Jumlah rata-rata pukulan home run per pemain dapat dihitung sebagai berikut:
Rata-rata = (8+15+22+21+12+9+11+27+14+13) / 10 = 15,2 sirkuit .
median
Median adalah nilai tengah dari suatu kumpulan data. Anda dapat mencari median dengan mengurutkan semua nilai individual dalam kumpulan data dari yang terkecil hingga yang terbesar dan mencari nilai mediannya. Jika jumlah nilainya ganjil, maka mediannya adalah nilai tengahnya. Jika banyaknya nilai genap, mediannya adalah rata-rata dari dua nilai tengah.
Misalnya, untuk mencari jumlah median home run yang dilakukan oleh 10 pemain bisbol pada contoh sebelumnya, kita dapat mengurutkan pemain dalam urutan menurun berdasarkan jumlah home run yang dilakukan:
| Pemain | #1 | #6 | #7 | #5 | #sepuluh | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|---|
| Home run | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
Karena jumlah nilai kita genap, median hanyalah rata-rata dari dua nilai tengah: 13.5 .
Sebaliknya, pertimbangkan jika kita memiliki sembilan pemain:
| Pemain | #1 | #6 | #7 | #5 | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|
| Home run | 8 | 9 | 11 | 12 | 14 | 15 | 21 | 22 | 27 |
Dalam kasus ini, karena jumlah nilai kita ganjil, median hanyalah nilai tengah: 14 .
Mode
Modus adalah nilai yang paling sering muncul dalam suatu kumpulan data. Suatu kumpulan data tidak boleh memiliki mode (jika tidak ada nilai yang berulang), satu mode, atau beberapa mode.
Misalnya, kumpulan data berikut tidak memiliki mode:
| Pemain | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #sepuluh |
|---|---|---|---|---|---|---|---|---|---|---|
| Home run | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
Kumpulan data berikut memiliki mode: 15 . Ini adalah nilai yang paling sering muncul.
| Pemain | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #sepuluh |
|---|---|---|---|---|---|---|---|---|---|---|
| Home run | 8 | 9 | 11 | 12 | 13 | 15 | 15 | 21 | 22 | 27 |
Kumpulan data berikut memiliki tiga mode: 8, 15, 19 . Inilah nilai-nilai yang paling sering muncul.
| Pemain | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #sepuluh |
|---|---|---|---|---|---|---|---|---|---|---|
| Home run | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
Mode dapat menjadi ukuran tendensi sentral yang sangat berguna ketika bekerja dengan data kategorikal, karena mode ini memberi tahu kita kategori mana yang paling sering muncul. Misalnya, perhatikan diagram batang berikut yang memperlihatkan hasil survei tentang warna favorit orang:
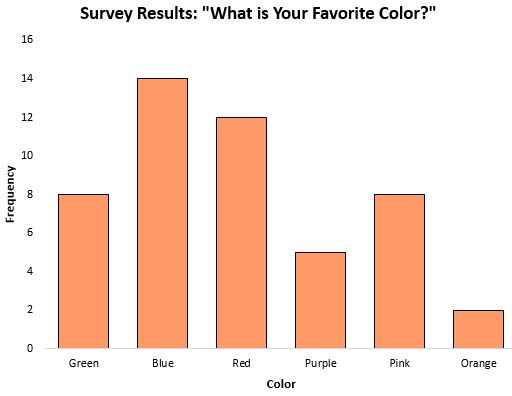
Modusnya , atau respons yang paling sering muncul, berwarna biru.
Dalam skenario yang datanya bersifat kategorikal (seperti di atas), median atau mean tidak dapat dihitung, sehingga modus adalah satu-satunya ukuran tendensi sentral yang dapat kita gunakan.
Mode ini juga dapat digunakan untuk data numerik, seperti yang kita lihat pada contoh di atas pada pemain bisbol. Namun, mode cenderung kurang berguna untuk menjawab pertanyaan “Berapa nilai tipikal kumpulan data ini?” »
Misalnya, kita ingin mengetahui jumlah rata-rata home run yang dilakukan oleh pemain bisbol di tim ini:
| Pemain | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #sepuluh |
|---|---|---|---|---|---|---|---|---|---|---|
| Home run | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
Modus untuk kumpulan data ini adalah 8, 15, dan 19 karena ini adalah nilai yang paling sering muncul. Namun, ini tidak terlalu membantu dalam memahami jumlah home run yang biasa dilakukan oleh seorang pemain dalam tim. Ukuran tendensi sentral yang lebih baik dalam hal ini adalah median (15) atau mean (juga 15).
Modus juga merupakan ukuran tendensi sentral yang buruk jika merupakan bilangan yang jauh dari nilai lainnya. Misalnya, mode kumpulan data berikut adalah 30, namun ini sebenarnya tidak mewakili jumlah home run “umumnya” per pemain dalam tim:
| Pemain | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #sepuluh |
|---|---|---|---|---|---|---|---|---|---|---|
| Home run | 5 | 6 | 7 | sepuluh | 11 | 12 | 13 | 15 | 30 | 30 |
Sekali lagi, mean atau median akan berfungsi lebih baik dalam menggambarkan lokasi pusat kumpulan data ini.
Kapan Menggunakan Mean, Median, dan Mode
Kita telah melihat bahwa mean, median, dan mode semuanya mengukur lokasi pusat, atau “nilai tipikal”, dari kumpulan data dengan cara yang sangat berbeda:
Rata-rata: Menemukan nilai rata-rata dalam kumpulan data.
Median: Menemukan nilai median dalam kumpulan data.
Mode: Menemukan nilai paling sering dalam kumpulan data.
Berikut adalah skenario dimana ukuran tendensi sentral tertentu lebih baik digunakan dibandingkan yang lain:
Kapan menggunakan rata-rata
Cara terbaik adalah menggunakan rata-rata ketika distribusi data cukup simetris dan tidak ada outlier.
Misalnya, kita mempunyai distribusi berikut yang menunjukkan gaji individu di kota tertentu:

Karena distribusi ini cukup simetris (yaitu jika Anda membaginya menjadi dua, masing-masing setengahnya akan terlihat kira-kira sama) dan tidak ada outlier (yaitu (katakanlah tidak ada gaji yang sangat tinggi), rata-rata akan berfungsi dengan baik dalam menggambarkan kumpulan data ini.
Rata-ratanya adalah $63.000, yang kira-kira berada di tengah distribusi:

Kapan menggunakan median
Cara terbaik adalah menggunakan median ketika distribusi data tidak seimbang atau ketika terdapat outlier.
Data yang bias:
Ketika distribusinya miring, median masih dapat menangkap lokasi pusat. Misalnya, perhatikan distribusi gaji individu di kota tertentu berikut ini:

Median lebih mencerminkan gaji “tipikal” seseorang dibandingkan rata-rata. Hal ini karena nilai yang besar pada bagian ekor suatu distribusi cenderung menjauhkan mean dari pusat menuju ekor yang panjang.
Dalam contoh khusus ini, rata-rata menunjukkan bahwa rata-rata individu berpenghasilan sekitar $47.000 per tahun di kota ini, sedangkan median menunjukkan bahwa rata-rata individu hanya berpenghasilan sekitar $32.000 per tahun, yang jauh lebih mewakili rata-rata individu.
Pencilan:
Median juga membantu menangkap lokasi pusat suatu distribusi dengan lebih baik ketika terdapat outlier dalam data. Misalnya, perhatikan grafik berikut yang menunjukkan luas persegi rumah di jalan tertentu:

Rata-rata sangat dipengaruhi oleh beberapa rumah yang sangat besar, sedangkan median tidak. Oleh karena itu, median berfungsi lebih baik dalam menangkap ukuran luas “tipikal” sebuah rumah di jalan tersebut dibandingkan rata-rata.
Kapan menggunakan mode
Mode ini paling baik digunakan saat Anda bekerja dengan data kategorikal dan ingin mengetahui kategori mana yang paling sering muncul. Berikut beberapa contohnya:
- Anda sedang melakukan survei tentang warna favorit orang-orang dan ingin mengetahui warna mana yang paling sering muncul dalam tanggapannya.
- Anda sedang melakukan survei terhadap preferensi orang-orang di antara tiga pilihan desain situs web dan ingin mengetahui desain mana yang paling disukai orang.
Seperti disebutkan sebelumnya, jika Anda bekerja dengan data kategorikal, median atau mean tidak dapat dihitung, sehingga modus menjadi satu-satunya ukuran tendensi sentral.
Secara umum, jika Anda bekerja dengan data numerik seperti luas rumah, jumlah pukulan home run per pemain, gaji per individu, dll., biasanya yang terbaik adalah menggunakan median atau rata-rata untuk menggambarkan nilai “tipikal” dalam kumpulan data.
Catatan: Penting untuk diperhatikan bahwa jika suatu kumpulan data terdistribusi normal sempurna , maka mean, median, dan modus semuanya memiliki nilai yang sama.