Cara menggunakan metode kuadrat terkecil di r

Metode kuadrat terkecil adalah metode yang dapat kita gunakan untuk mencari garis regresi yang paling sesuai dengan kumpulan data tertentu.

Untuk menggunakan metode kuadrat terkecil agar sesuai dengan garis regresi di R, kita dapat menggunakan fungsi lm() .

Fungsi ini menggunakan sintaks dasar berikut:

 model <- lm(response ~ predictor, data=df)

Contoh berikut menunjukkan cara menggunakan fungsi ini di R.

Contoh: metode kuadrat terkecil di R

Misalkan kita mempunyai kerangka data berikut di R yang menunjukkan jumlah jam belajar dan nilai ujian yang sesuai untuk 15 siswa dalam satu kelas:

 #create data frame
df <- data. frame (hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14),
                 score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89))

#view first six rows of data frame
head(df)

  hours score
1 1 64
2 2 66
3 4 76
4 5 73
5 5 74
6 6 81

Kita dapat menggunakan fungsi lm() untuk menggunakan metode kuadrat terkecil agar sesuai dengan garis regresi ke data ini:

 #use method of least squares to fit regression line
model <- lm(score ~ hours, data=df)

#view regression model summary
summary(model)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
   Min 1Q Median 3Q Max 
-5,140 -3,219 -1,193 2,816 5,772 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 65,334 2,106 31,023 1.41e-13 ***
hours 1.982 0.248 7.995 2.25e-06 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.641 on 13 degrees of freedom
Multiple R-squared: 0.831, Adjusted R-squared: 0.818 
F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06

Dari nilai-nilai pada kolom Estimasi Hasil, kita dapat menuliskan garis regresi yang sesuai sebagai berikut:

Nilai ujian = 65.334 + 1.982 (jam)

Berikut cara menginterpretasikan setiap koefisien dalam model:

• Intercept : Untuk siswa yang belajar 0 jam, nilai ujian yang diharapkan adalah 65.334 .
• jam : Untuk setiap jam tambahan belajar, nilai ujian yang diharapkan meningkat sebesar 1,982 .

Kita dapat menggunakan persamaan ini untuk memperkirakan nilai ujian yang akan diterima siswa berdasarkan jam belajarnya.

Misalnya, jika seorang siswa belajar selama 5 jam, kami memperkirakan nilai ujiannya adalah 75.244:

Nilai Ujian = 65.334 + 1.982(5) = 75.244

Terakhir, kita dapat membuat plot sebar dari data asli dengan garis regresi yang dipasang ditumpangkan pada plot:

 #create scatter plot of data
plot(df$hours, df$score, pch=16, col=' steelblue ')

#add fitted regression line to scatter plot
abline(model)

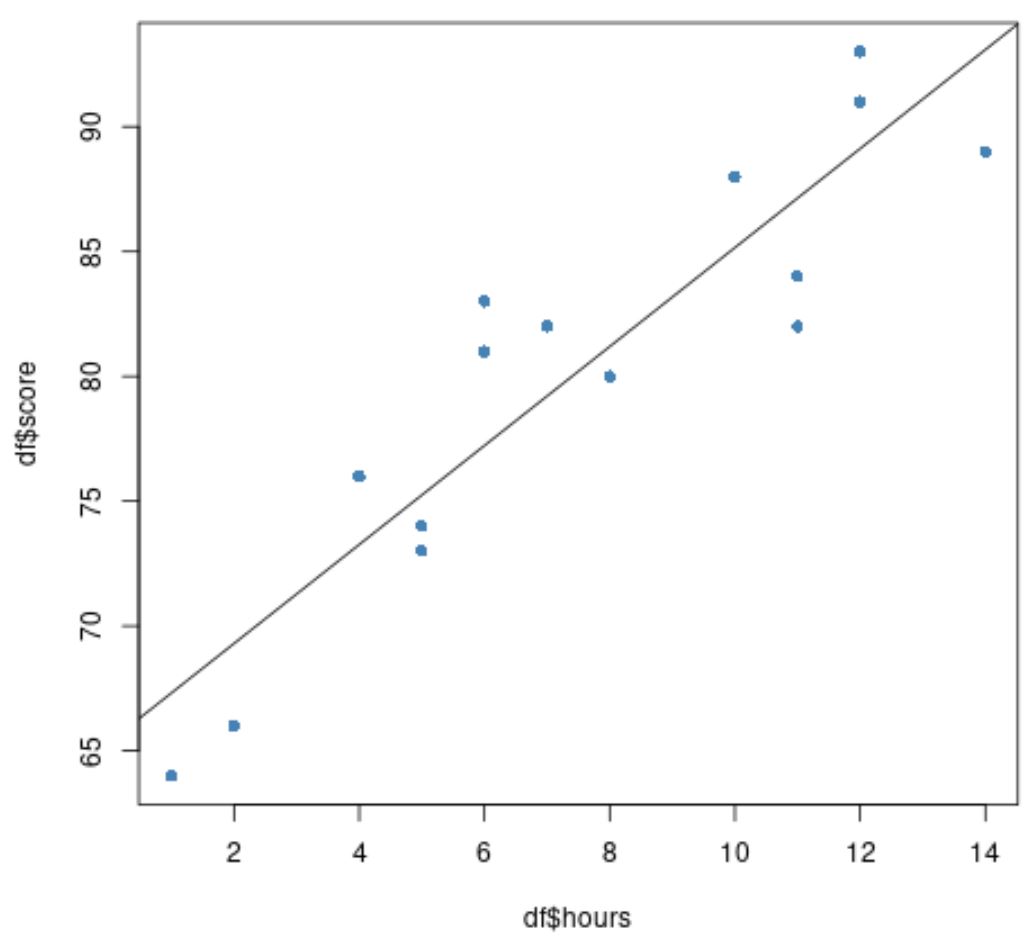
Lingkaran biru melambangkan data dan garis hitam melambangkan garis regresi yang sesuai.

Sumber daya tambahan

Tutorial berikut menjelaskan cara melakukan tugas umum lainnya di R:

Cara membuat plot sisa di R
Cara menguji multikolinearitas di R
Cara melakukan pemasangan kurva di R