Mode (statistik)

Oleh Benjamin anderson Agustus 5, 2023 Statistik 0 Komentar

Artikel ini menjelaskan apa itu mode dalam statistik. Anda akan mempelajari cara menemukan modus statistik untuk data yang dikelompokkan dan data yang tidak dikelompokkan, berbagai jenis modus, dan beberapa contoh ukuran statistik ini.

Apa modus dalam statistik?

Dalam statistik, modus adalah nilai dalam kumpulan data yang mempunyai frekuensi absolut tertinggi, yaitu modus adalah nilai yang paling sering diulang dalam suatu kumpulan data.

Oleh karena itu, untuk menghitung mode kumpulan data statistik, cukup hitung berapa kali setiap elemen data muncul dalam sampel, dan data yang paling sering diulang akan menjadi modenya.

Modus digunakan untuk menentukan distribusi statistik, karena nilai yang paling sering diulang biasanya berada di tengah distribusi.

Modusnya juga dapat dikatakan sebagai modus statistik atau nilai modal . Demikian pula, ketika data dikelompokkan ke dalam interval, interval yang paling sering diulang adalah interval modal atau kelas modal .

Secara umum istilah Mo digunakan sebagai lambang modus statistik, misalnya modus distribusi X adalah Mo(X).

Perlu diingat bahwa modus adalah ukuran statistik posisi tengah, serta median dan mean. Di bawah ini kita akan melihat arti dari masing-masing ukuran statistik tersebut.

Jenis mode dalam statistik

Dalam statistik, ada beberapa jenis mode yang diklasifikasikan menurut jumlah nilai yang paling sering diulang:

Mode unimodal : hanya ada satu nilai dengan jumlah pengulangan maksimum. Misalnya, [1, 4, 2, 4, 5, 3].
Mode bimodal : Jumlah pengulangan maksimum terjadi pada dua nilai berbeda, dan kedua nilai diulang dalam jumlah yang sama. Misalnya, [2, 6, 7, 2, 3, 6, 9].
Mode multimodal : Tiga nilai atau lebih memiliki jumlah pengulangan maksimum yang sama. Misalnya, [3, 3, 4, 1, 3, 4, 2, 1, 4, 5, 2, 1].

Cara menemukan mode statistik

Untuk menemukan mode statistik suatu kumpulan data, Anda harus mengikuti langkah-langkah berikut:

Urutkan datanya. Langkah ini tidak wajib, namun akan mempermudah penghitungan angka.
Hitung berapa kali setiap angka muncul.
Angka yang paling sering muncul adalah mode statistik.

Contoh mode statistik

Mengingat pengertian fashion dalam statistik, di bawah ini Anda dapat melihat contoh masing-masing jenis fashion agar Anda dapat lebih memahami konsepnya.

Contoh mode unimodal

Apa mode dari kumpulan data berikut?

$5 \ 4 \ 9 \ 7 \ 2 \ 3 \ 9 \ 6 \ 5 \ 2 \ 5$

Nomornya tidak berurutan, jadi kita urutkan terlebih dahulu agar lebih mudah mencari modusnya.

$2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 7 \ 9 \ 9$

Angka 2 dan 9 muncul dua kali, namun angka 5 terulang tiga kali. Oleh karena itu, modus deret datanya adalah nomor 5.

$Mo=5$

Contoh modus bimodal

Hitung mode kumpulan data berikut:

$8 \ 7 \ 0 \ 6 \ 10 \ 9 \ 13 \ 8 \ 0 \ 6 \ 2 \ 6 \ 5 \ 11 \ 10$

$0 \ 9 \ 8 \ 6 \ 12 \ 3 \ 5 \ 11 \ 1 \ 4 \ 8 \ 10 \ 2 \ 5 \ 7$

Pertama kita urutkan angkanya:

$0 \ 0 \ 0 \ 1 \ 2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 6 \ 6 \ 6$

$7 \ 7 \ 8 \ 8 \ 8 \ 8 \ 9 \ 9 \ 10 \ 10 \ 10 \ 11 \ 11 \ 12 \ 13$

Seperti yang Anda lihat, angka 6 dan angka 8 muncul sebanyak empat kali, yang merupakan jumlah pengulangan maksimum. Oleh karena itu, dalam hal ini adalah mode bimodal dan kedua angka tersebut adalah mode kumpulan data:

$Mo=\{ 6 \ ; \ 8\}$

Contoh mode multimoda

Temukan mode kumpulan data berikut:

$21 \ 27 \ 32 \ 15 \ 13 \ 20 \ 21 \ 21 \ 25 \ 27 \ 31 \ 30 \ 19 \ 20 \ 16$

$22 \ 19 \ 20 \ 31 \ 18 \ 20 \ 25 \ 26 \ 15 \ 20 \ 31 \ 31 \ 27 \ 16 \ 17$

$31 \ 27 \ 24 \ 23 \ 21 \ 27 \ 29 \ 36 \ 32 \ 30 \ 16 \ 22 \ 15 \ 14 \ 37$

Karena datanya banyak, maka kita urutkan dulu dalam urutan menaik agar lebih mudah menghitungnya:

$13 \ 14 \ 15\ 15\ 15 \ 16 \ 16 \ 16 \ 17 \ 18 \ 19 \ 19 \ 20 \ 20 \ 20$

$20 \ 20 \ 21 \ 21 \ 21\ 21 \ 22 \ 22 \ 23 \ 24 \ 25 \ 25 \ 26 \ 27 \ 27$

$27 \ 27 \ 27 \ 29 \ 30 \ 30 \ 31 \ 31 \ 31 \ 31 \ 31 \ 32 \ 32 \ 36 \ 37$

Angka yang paling banyak diulang adalah 20, 27 dan 31, ketiga angka tersebut diulang sebanyak lima kali. Oleh karena itu, modus contoh ini adalah multimodal.

$Mo=\{ 20 \ ; \ 27 \ ; \ 31\}$

kalkulator mode

Masukkan data dari sampel statistik apa pun ke dalam kalkulator online berikut untuk menghitung modusnya. Data harus dipisahkan dengan spasi dan dimasukkan menggunakan titik sebagai pemisah desimal.

Mode untuk data yang dikelompokkan

Ketika kita mengelompokkan data dalam bentuk interval, kita tidak mengetahui berapa kali setiap bagian data diulang, yang kita tahu hanyalah frekuensi setiap interval.

Jadi, untuk menghitung modus data yang dikelompokkan ke dalam interval, kita harus menggunakan rumus berikut :

$Mo=L_i+ \cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i$

Emas:

L _i adalah batas bawah interval modal (interval frekuensi absolut tertinggi).
f _i adalah frekuensi absolut dari interval modal.
f _i-1 adalah frekuensi absolut dari interval sebelum modal.
f _i+1 adalah frekuensi absolut interval setelah modal.
A _i adalah lebar interval modal.

Sebagai contoh, di bawah ini Anda telah menyelesaikan latihan yang mode datanya dikelompokkan ke dalam interval dihitung:

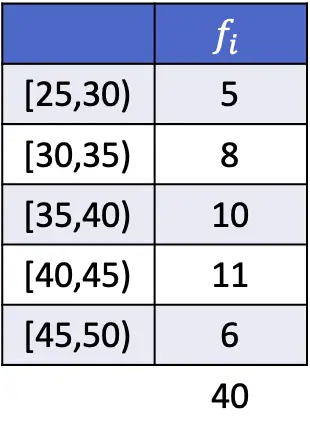
contoh mode statistik untuk data yang dikelompokkan

Dalam hal ini, interval modalnya adalah [40,45), karena merupakan interval dengan frekuensi absolut terbesar. Oleh karena itu, parameter rumus mode untuk data yang dikelompokkan adalah:

$\begin{array}{c}L_i=40\\[2ex]f_i=11\\[2ex]f_{i-1}=10\\[2ex]f_{i+1}=6\\[2ex]A_i=5\end{array}$

Oleh karena itu kami menerapkan rumus untuk menentukan mode data yang dikelompokkan ke dalam interval dan kami melakukan perhitungan:

$\begin{aligned}Mo & =L_i+ \cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i\\[2ex]& =40+ \cfrac{11-10}{(11-10)+(11-6)}\cdot 5\\[2ex]&=40,83\end{aligned}$

Perbedaan antara modus, mean dan median

Pada bagian terakhir ini kita akan melihat apa perbedaan antara modus, mean, dan median. Karena ketiganya merupakan ukuran statistik posisi sentral, artinya berbeda.

Seperti yang dijelaskan di seluruh artikel, modus dalam matematika adalah nilai yang paling sering diulang dalam suatu kumpulan data.

Kedua, mean adalah nilai rata-rata seluruh data statistik. Jadi, untuk memperoleh rata-rata data tertentu, Anda harus menjumlahkan seluruh data kemudian membagi hasilnya dengan jumlah observasi.

Dan yang terakhir, median adalah nilai yang menempati posisi sentral pada saat data diurutkan.

Dengan demikian, ketiga ukuran statistik membantu menentukan distribusi probabilitas, karena memberikan gambaran tentang nilai-nilai sentralnya. Namun perlu diingat bahwa tidak ada satu ukuran yang lebih baik dari yang lain, yang ada hanyalah konsep yang berbeda.

Properti mode

Properti fesyen tersebut adalah:

Modusnya dapat ditemukan baik pada variabel kuantitatif maupun variabel kualitatif.
Jika kita menerapkan transformasi linier pada variabel acak, nilai mean akan berubah bergantung pada operasi yang diterapkan.

$Mo(X)=Y \ \color{orange}\bm{\longrightarrow}\color{black} \ M(aX+b)=aY+b$

Secara umum, mode ini tidak sensitif terhadap outlier.
Jika semua nilai mempunyai frekuensi yang sama maka tidak ada modus.

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya