Apa yang dimaksud dengan multikolinearitas sempurna? (definisi & contoh)

Dalam statistik, multikolinearitas terjadi ketika dua atau lebih variabel prediktor berkorelasi tinggi satu sama lain, sehingga tidak memberikan informasi unik atau independen dalam model regresi.

Jika tingkat korelasi antar variabel cukup tinggi, hal ini dapat menimbulkan masalah saat menyesuaikan dan menafsirkan model regresi.

Kasus multikolinearitas yang paling ekstrem disebut multikolinearitas sempurna . Hal ini terjadi ketika dua atau lebih variabel prediktor mempunyai hubungan linier yang tepat satu sama lain.

Misalnya, kita memiliki kumpulan data berikut:

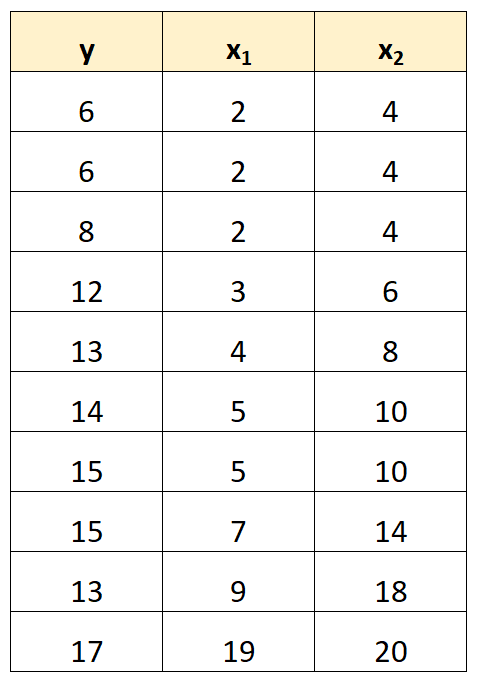
Perhatikan bahwa nilai variabel prediktor x ₂ hanyalah nilai x ₁ dikalikan 2.

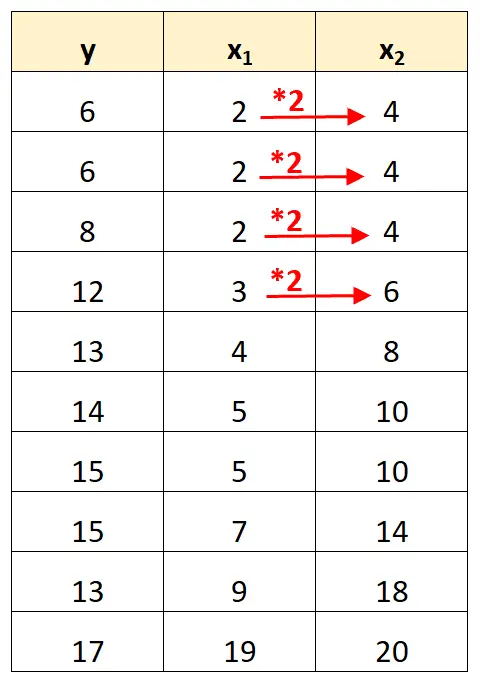
Ini adalah contoh multikolinearitas sempurna .

Masalah multikolinearitas sempurna

Ketika terdapat multikolinearitas sempurna dalam kumpulan data, kuadrat terkecil biasa tidak dapat menghasilkan estimasi koefisien regresi.

Memang benar bahwa tidak mungkin memperkirakan pengaruh marjinal suatu variabel prediktor (x ₁ ) terhadap variabel respons (y) sambil menjaga variabel prediktor lainnya (x ₂ ) tetap konstan karena x ₂ selalu bergerak tepat pada saat x ₁ bergerak.

Singkatnya, multikolinearitas sempurna membuat tidak mungkin memperkirakan nilai setiap koefisien dalam model regresi.

Cara mengatasi multikolinearitas sempurna

Cara paling sederhana untuk menangani multikolinearitas sempurna adalah dengan menghilangkan salah satu variabel yang mempunyai hubungan linier eksak dengan variabel lainnya.

Misalnya, pada kumpulan data sebelumnya, kita cukup menghapus x ₂ sebagai variabel prediktor.

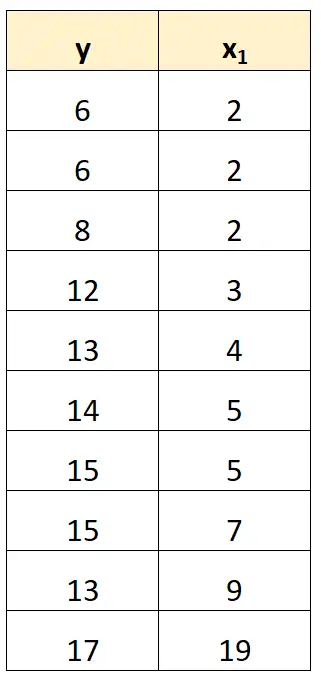
Kami kemudian akan menyesuaikan model regresi menggunakan x ₁ sebagai variabel prediktor dan y sebagai variabel respon.

Contoh multikolinearitas sempurna

Contoh berikut menunjukkan tiga skenario multikolinearitas sempurna yang paling umum dalam praktiknya.

1. Variabel prediktor merupakan kelipatan variabel lainnya

Katakanlah kita ingin menggunakan “tinggi dalam sentimeter” dan “tinggi dalam meter” untuk memprediksi berat spesies lumba-lumba tertentu.

Seperti inilah tampilan kumpulan data kami:

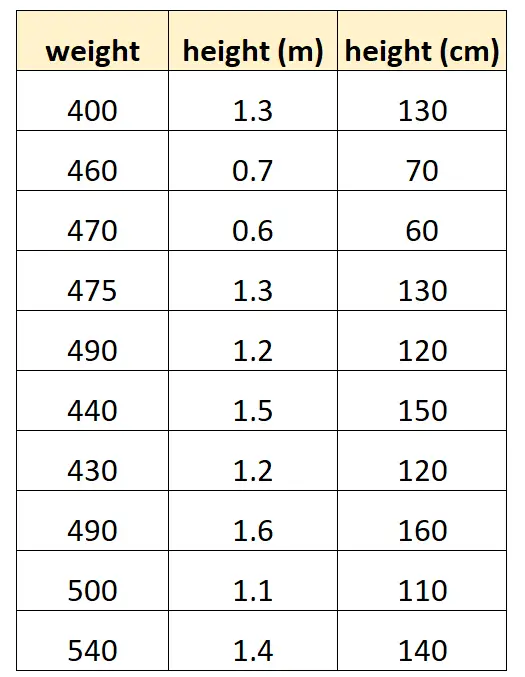
Perhatikan bahwa nilai “tinggi dalam sentimeter” sama dengan “tinggi dalam meter” dikalikan dengan 100. Ini adalah kasus multikolinearitas sempurna.

Jika kita mencoba menyesuaikan model regresi linier berganda di R menggunakan kumpulan data ini, kita tidak akan dapat menghasilkan estimasi koefisien untuk variabel prediktor “meter”:

 #define data
df <- data. frame (weight=c(400, 460, 470, 475, 490, 440, 430, 490, 500, 540),
                 m=c(1.3, .7, .6, 1.3, 1.2, 1.5, 1.2, 1.6, 1.1, 1.4),
                 cm=c(130, 70, 60, 130, 120, 150, 120, 160, 110, 140))

#fit multiple linear regression model
model <- lm(weight~m+cm, data=df)

#view summary of model
summary(model)

Call:
lm(formula = weight ~ m + cm, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-70,501 -25,501 5,183 19,499 68,590 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 458,676 53,403 8,589 2.61e-05 ***
m 9.096 43.473 0.209 0.839    
cm NA NA NA NA    
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 41.9 on 8 degrees of freedom
Multiple R-squared: 0.005442, Adjusted R-squared: -0.1189 
F-statistic: 0.04378 on 1 and 8 DF, p-value: 0.8395

2. Variabel prediktor adalah versi transformasi dari variabel lain

Katakanlah kita ingin menggunakan “poin” dan “poin berskala” untuk memprediksi rating pemain bola basket.

Misalkan variabel “titik berskala” dihitung sebagai:

Poin berskala = (poin – μ _poin ) / σ _poin

Seperti inilah tampilan kumpulan data kami:

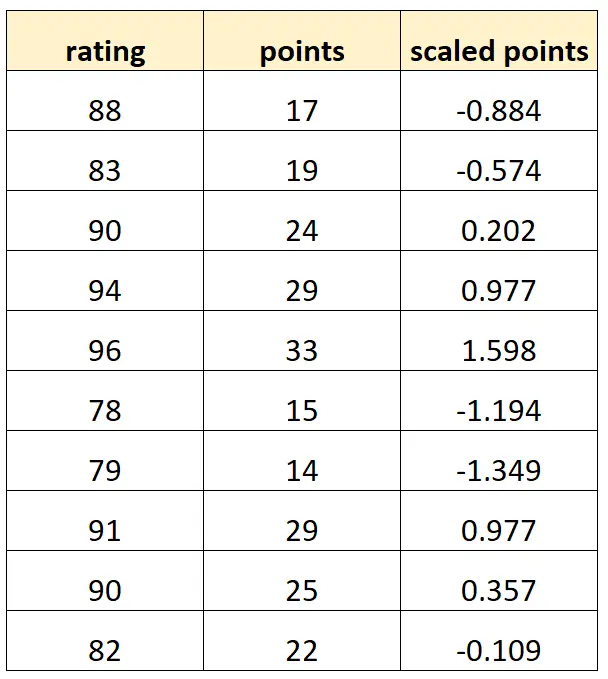
Perhatikan bahwa setiap nilai “poin berskala” hanyalah versi standar dari “poin”. Ini adalah kasus multikolinearitas sempurna.

Jika kami mencoba menyesuaikan model regresi linier berganda di R menggunakan kumpulan data ini, kami tidak akan dapat menghasilkan estimasi koefisien untuk variabel prediktor “titik berskala”:

 #define data
df <- data. frame (rating=c(88, 83, 90, 94, 96, 78, 79, 91, 90, 82),
                 pts=c(17, 19, 24, 29, 33, 15, 14, 29, 25, 22))

df$scaled_pts <- (df$pts - mean(df$pts)) / sd(df$pts)

#fit multiple linear regression model
model <- lm(rating~pts+scaled_pts, data=df)

#view summary of model
summary(model)

Call:
lm(formula = rating ~ pts + scaled_pts, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-4.4932 -1.3941 -0.2935 1.3055 5.8412 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 67.4218 3.5896 18.783 6.67e-08 ***
pts 0.8669 0.1527 5.678 0.000466 ***
scaled_pts NA NA NA NA    
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.953 on 8 degrees of freedom
Multiple R-squared: 0.8012, Adjusted R-squared: 0.7763 
F-statistic: 32.23 on 1 and 8 DF, p-value: 0.0004663

3. Perangkap variabel tiruan

Skenario lain di mana multikolinearitas sempurna dapat terjadi dikenal sebagai perangkap variabel dummy . Ini adalah saat kita ingin mengambil variabel kategori dalam model regresi dan mengubahnya menjadi “variabel dummy” yang bernilai 0, 1, 2, dst.

Misalnya, kita ingin menggunakan variabel prediktor “usia” dan “status perkawinan” untuk memprediksi pendapatan:

Untuk menggunakan “status perkawinan” sebagai variabel prediktor, terlebih dahulu kita harus mengubahnya menjadi variabel dummy.

Untuk melakukan ini, kita dapat membiarkan “Lajang” sebagai nilai dasar, karena ini paling sering terjadi, dan menetapkan nilai 0 atau 1 untuk “Menikah” dan “Perceraian” sebagai berikut:

Kesalahannya adalah membuat tiga variabel dummy baru sebagai berikut:

Dalam hal ini, variabel “Lajang” merupakan kombinasi linier sempurna dari variabel “Menikah” dan “Cerai”. Ini adalah contoh multikolinearitas sempurna.

Jika kami mencoba menyesuaikan model regresi linier berganda di R menggunakan kumpulan data ini, kami tidak akan dapat menghasilkan estimasi koefisien untuk setiap variabel prediktor:

 #define data
df <- data. frame (income=c(45, 48, 54, 57, 65, 69, 78, 83, 98, 104, 107),
                 age=c(23, 25, 24, 29, 38, 36, 40, 59, 56, 64, 53),
                 single=c(1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0),
                 married=c(0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1),
                 divorced=c(0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0))

#fit multiple linear regression model
model <- lm(income~age+single+married+divorced, data=df)

#view summary of model
summary(model)

Call:
lm(formula = income ~ age + single + married + divorced, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-9.7075 -5.0338 0.0453 3.3904 12.2454 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)   
(Intercept) 16.7559 17.7811 0.942 0.37739   
age 1.4717 0.3544 4.152 0.00428 **
single -2.4797 9.4313 -0.263 0.80018   
married NA NA NA NA   
divorced -8.3974 12.7714 -0.658 0.53187   
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 8.391 on 7 degrees of freedom
Multiple R-squared: 0.9008, Adjusted R-squared: 0.8584 
F-statistic: 21.2 on 3 and 7 DF, p-value: 0.0006865

Sumber daya tambahan

Panduan Multikolinearitas dan VIF dalam Regresi
Cara menghitung VIF di R
Cara menghitung VIF dengan Python
Cara menghitung VIF di excel