Perbedaan nilai z dan nilai p dalam statistik

Dua istilah yang sering membingungkan siswa dalam statistika adalah nilai-z dan nilai-p .

Untuk memahami perbedaan antara istilah-istilah ini, ada baiknya untuk memahami z test .

Ada dua jenis tes z yang umum:

• Uji z satu sampel : Digunakan untuk menguji apakah rata-rata populasi sama dengan nilai tertentu.
• Uji z dua sampel : Digunakan untuk menguji apakah rata-rata dua populasi sama.

Kami menggunakan langkah-langkah berikut untuk melakukan setiap pengujian:

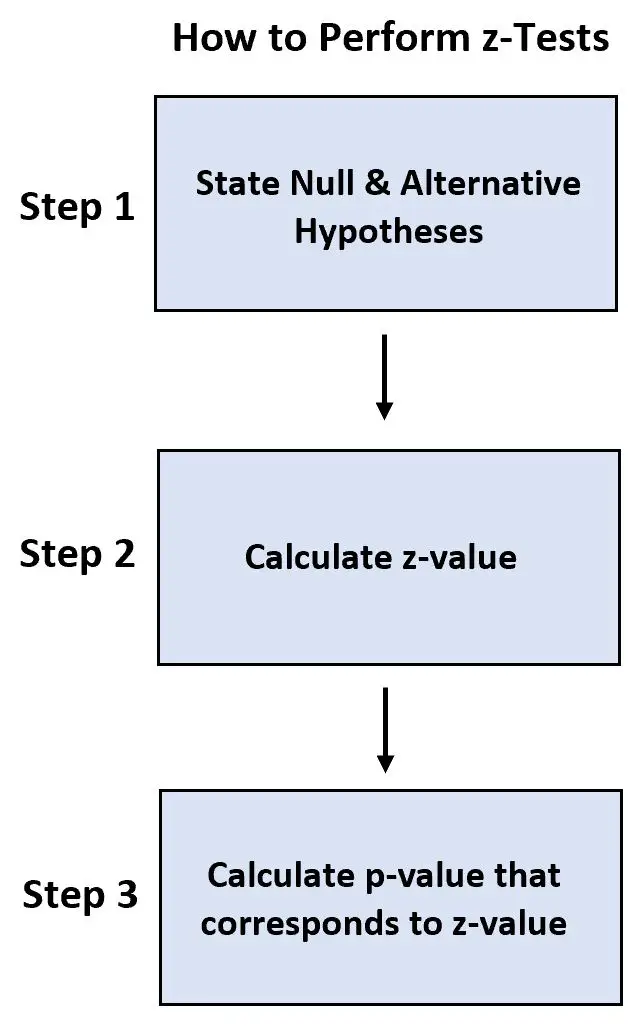
• Langkah 1: Nyatakan hipotesis nol dan hipotesis alternatif.
• Langkah 2: Hitung nilai z.
• Langkah 3: Hitung nilai p yang sesuai dengan nilai z.

Untuk setiap pengujian, nilai z adalah cara untuk mengukur perbedaan antara rata-rata populasi dan nilai p adalah probabilitas memperoleh nilai z dengan nilai absolut setidaknya sebesar yang sebenarnya kita amati dalam sampel. data jika hipotesis nol benar.

Jika p-value kurang dari nilai tertentu (misalnya 0,05), maka hipotesis nol pengujian tersebut ditolak .

Untuk setiap jenis uji z, kami tertarik pada nilai p dan kami cukup menggunakan nilai z sebagai langkah perantara untuk menghitung nilai p.

Contoh berikut menunjukkan cara menghitung dan menafsirkan nilai-z dan nilai-p yang sesuai untuk uji-z dua sampel.

Contoh: Menghitung dan Menafsirkan Nilai Z dan Nilai P

Asumsikan tingkat IQ individu dari dua kota berbeda berdistribusi normal, masing-masing dengan standar deviasi populasi 15.

Seorang ilmuwan ingin mengetahui apakah rata-rata tingkat IQ antara individu di kota A dan kota B berbeda. Oleh karena itu, dia memilih sampel acak sederhana yang terdiri dari 20 orang dari setiap kota dan mencatat tingkat IQ mereka:

Kota A : 82, 84, 85, 89, 91, 91, 92, 94, 99, 99, 105, 109, 109, 109, 110, 112, 112, 113, 114, 114

Kota B : 90, 91, 91, 91, 95, 95, 99, 99, 108, 109, 109, 114, 115, 116, 117, 117, 128, 129, 130, 133

Berikut cara melakukan pengujian z dua sampel menggunakan data ini:

Langkah 1: Nyatakan hipotesis nol dan hipotesis alternatif.

Pertama, kami akan menyatakan hipotesis nol dan hipotesis alternatif:

• H ₀ : μ ₁ = μ ₂ (rata-rata kedua populasi adalah sama)
• H ₁ : μ ₁ ≠ μ ₂ (rata-rata dua populasi tidak sama)

Langkah 2: Hitung nilai z.

Selanjutnya, kita akan melakukan uji z dua sampel di Excel menggunakan data ini dan menemukan bahwa nilai z adalah -1.71817 .

Langkah 3: Hitung nilai p.

Kita dapat menggunakan kalkulator skor Z ke nilai P untuk menemukan bahwa nilai p yang sesuai dengan nilai az -1,71817 adalah 0,08577.

Karena nilai p ini tidak kurang dari 0,05, kita tidak mempunyai cukup bukti untuk menolak hipotesis nol.

Dengan demikian, kami menyimpulkan bahwa rata-rata tingkat IQ antara kedua kota tersebut tidak berbeda secara signifikan.

Perhatikan bahwa kami hanya menggunakan nilai z sebagai langkah perantara untuk menghitung nilai p.

Nilai p adalah nilai sebenarnya yang kami minati, namun kami harus menghitung nilai z terlebih dahulu.

Sumber daya tambahan

Tutorial berikut menjelaskan cara melakukan uji-z menggunakan berbagai perangkat lunak statistik:

Bagaimana Melakukan Tes Z di Excel
Cara melakukan tes Z di R
Cara Melakukan Tes Z dengan Python