Operasi pada himpunan: gabungan, perpotongan, komplemen, dan selisih

Himpunan adalah kumpulan elemen.

Kita menandai suatu himpunan dengan huruf kapital dan mendefinisikan elemen-elemen himpunan tersebut dengan menggunakan tanda kurung kurawal. Misalnya, kita mempunyai himpunan bernama “A” dengan elemen 1, 2, 3. Kita akan menuliskannya sebagai berikut:

SEBUAH = {1, 2, 3}

Tutorial ini menjelaskan operasi himpunan yang paling umum digunakan dalam probabilitas dan statistik.

Persatuan

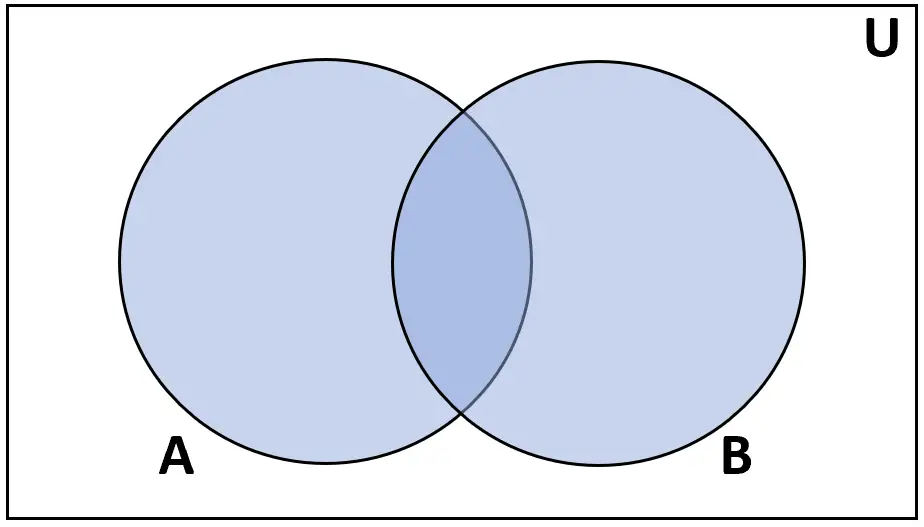
Definisi: Gabungan himpunan A dan B adalah himpunan yang anggota-anggotanya terdapat di A atau di B.

Peringkat: A ∪ B

Contoh:

• {1, 2, 3} ∪ {4, 5, 6} = {1, 2, 3, 4, 5, 6}
• {1, 2} ∪ {1, 2} = {1, 2}
• {1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}

Persimpangan

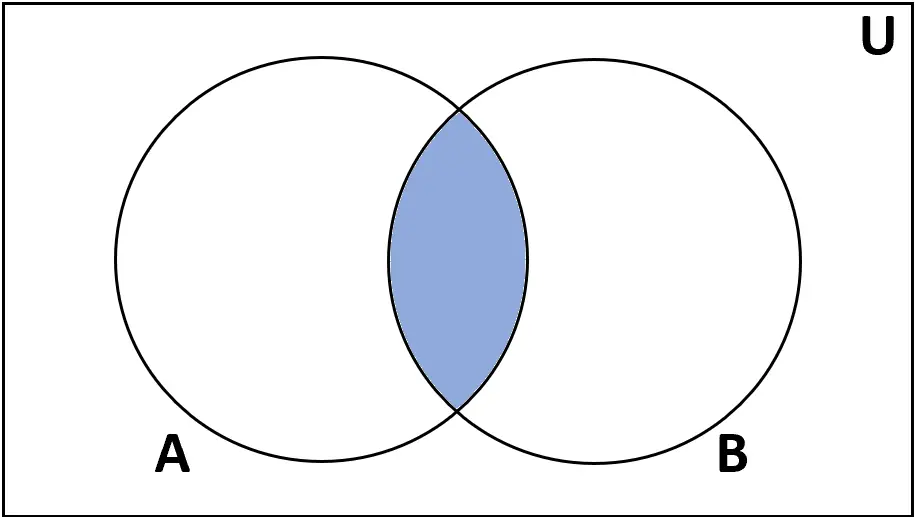
Definisi: Perpotongan himpunan A dan B adalah himpunan yang anggotanya terdapat pada A dan B.

Notasi: A ∩ B

Contoh:

• {1, 2, 3} ∩ {4, 5, 6} = {∅}
• {1, 2} ∩ {1, 2} = {1, 2}
• {1, 2, 3} ∩ {3, 4} = {3}

Melengkapi

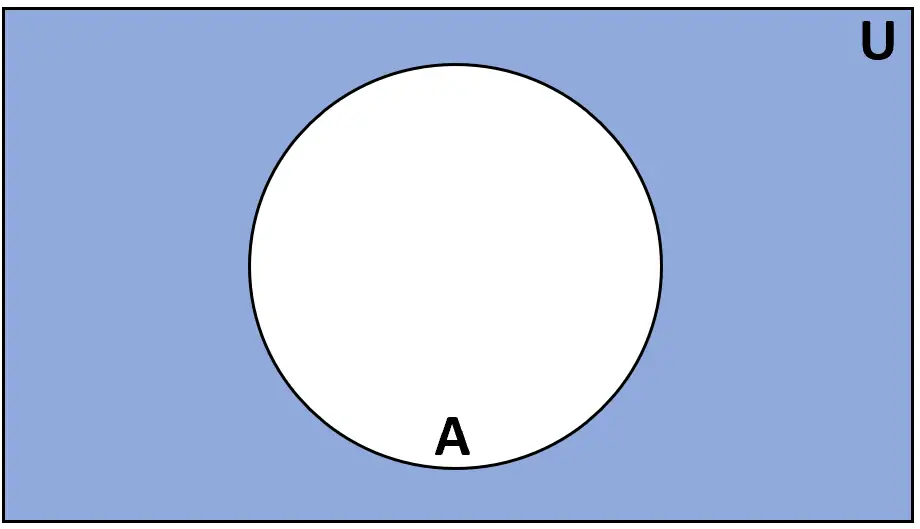
Definisi: Komplemen himpunan A adalah himpunan anggota-anggota yang termasuk dalam himpunan semesta U tetapi tidak termasuk dalam A.

Peringkat: A’ atau ^Ac

Contoh:

• Jika U = {1, 2, 3, 4, 5, 6} dan A = {1, 2}, maka A ^c = {3, 4, 5, 6}
• Jika U = {1, 2, 3} dan A = {1, 2}, maka A ^c = {3}

Perbedaan

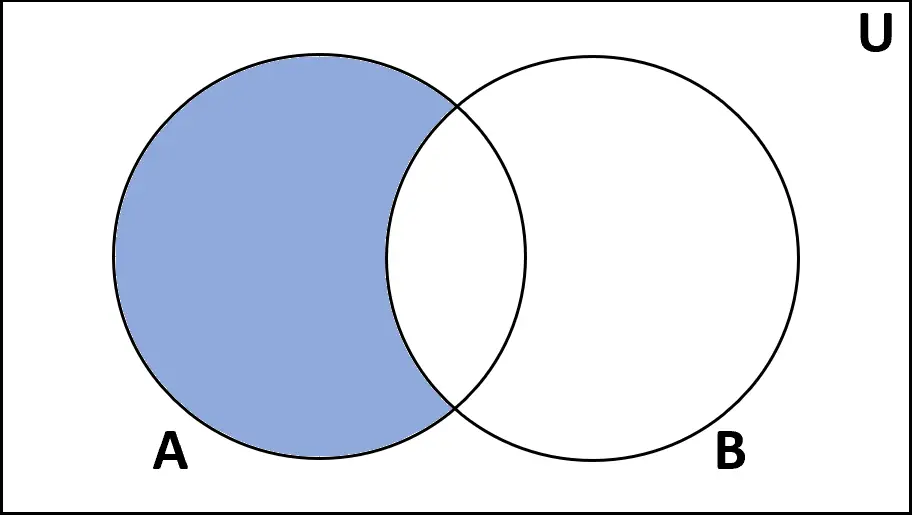
Definisi: Selisih himpunan A dan B adalah himpunan yang anggotanya terdapat di A tetapi tidak terdapat di B.

Peringkat: A–B

Contoh:

• {1, 2, 3} – {2, 3, 4} = {1}
• {1, 2} – {1, 2} = {∅}
• {1, 2, 3} – {4, 5} = {1, 2, 3}

Perbedaan simetris

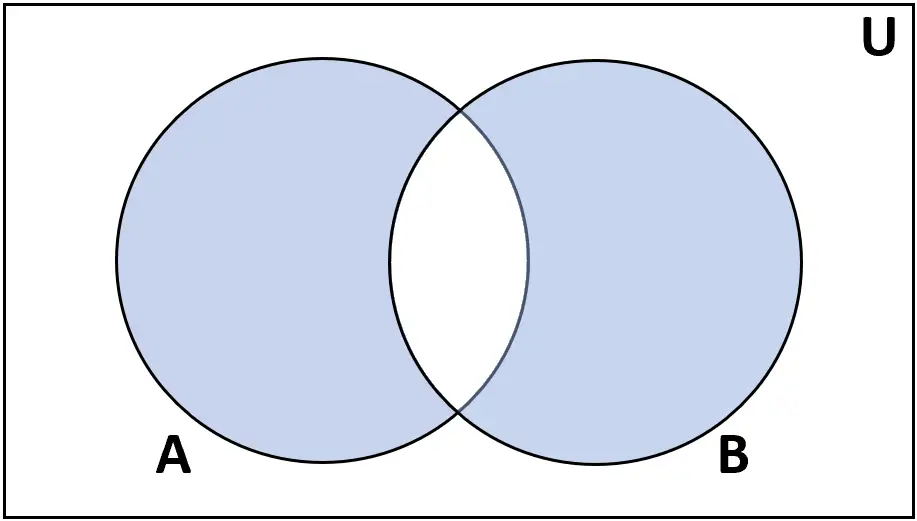
Definisi: Beda simetris himpunan A dan B adalah himpunan yang anggotanya terdapat pada A atau B, tetapi tidak keduanya.

Peringkat: AΔB

Contoh:

• {1, 2, 3} Δ {2, 3, 4} = {1, 4}
• {1, 2} Δ {1, 2} = {∅}
• {1, 2, 3} Δ {4, 5} = {1, 2, 3, 4, 5}

produk kartesius

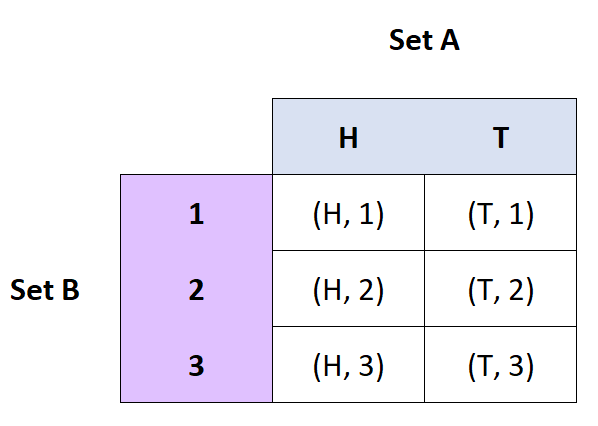
Definisi: Hasil kali kartesius himpunan A dan B adalah himpunan pasangan terurut A dan B.

Peringkat: A x B

Contoh:

• Jika A = {H, T} dan B = {1, 2, 3}, maka A x B = {(H, 1), (H, 2), (H, 3), (T, 1), ( T, 2), (T, 3)}
• Jika A = {T, H} dan B = {1, 2, 3}, maka A x B = {(T, 1), (T, 2), (T, 3), (H, 1), ( H, 2), (H, 3)}