Apakah rentang antarkuartil (iqr) dipengaruhi oleh outlier?

Dalam statistik, kita sering ingin mengetahui seberapa luas nilai “tersebar” dalam suatu distribusi.

Cara populer untuk mengukur penyebaran adalah rentang antarkuartil , yang dihitung sebagai selisih antara kuartil pertama dan kuartil ketiga dari kumpulan data. Kuartil hanyalah nilai yang membagi kumpulan data menjadi empat bagian yang sama.

Contoh: Perhitungan rentang antarkuartil

Contoh berikut menunjukkan cara menghitung rentang interkuartil untuk kumpulan data tertentu:

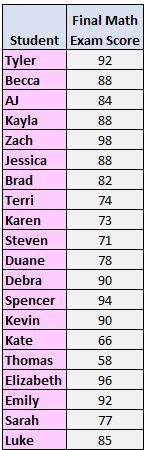
Langkah 1: Urutkan nilainya dari terkecil hingga terbesar.

58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

2. Temukan mediannya.

58, 66, 71, 73, 74, 77 , 78 , 82 , 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

Dalam hal ini, mediannya adalah antara 85 dan 88.

3. Median membagi kumpulan data menjadi dua bagian. Median bagian bawah adalah kuartil bawah dan median bagian atas adalah kuartil atas:

58, 66, 71 , 73 , 74 , 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

4. Hitung rentang antarkuartil.

Dalam hal ini, kuartil pertama adalah rata-rata dari dua nilai tengah di paruh bawah kumpulan data (75,5) dan kuartil ketiga adalah rata-rata dari dua nilai tengah di paruh atas kumpulan data. (91).

Jadi rentang antarkuartilnya adalah 91 – 75,5 = 15,5

Rentang antarkuartil tidak terpengaruh oleh outlier

Salah satu alasan orang lebih memilih menggunakan rentang interkuartil (IQR) saat menghitung “sebaran” suatu kumpulan data adalah karena rentang tersebut kuat terhadap outlier. Karena IQR hanyalah kisaran 50% tengah dari nilai data, maka IQR tidak terpengaruh oleh outlier ekstrem .

Untuk mendemonstrasikannya, pertimbangkan kumpulan data berikut:

[1, 4, 8, 11, 13, 17, 17, 20]

Berikut adalah metrik propagasi yang berbeda untuk kumpulan data ini:

• Rentang interkuartil: 11
• Kisaran: 19
• Deviasi standar: 6.26
• Perbedaan: 39.23

Sekarang pertimbangkan kumpulan data yang sama tetapi dengan tambahan outlier ekstrim:

[1, 4, 8, 11, 13, 17, 17, 20, 150 ]

Berikut adalah metrik propagasi yang berbeda untuk kumpulan data ini:

• Rentang interkuartil: 12,5
• Kisaran: 149
• Deviasi standar: 43,96
• Sebaran: 1.932,84

Perhatikan bagaimana rentang antarkuartil hanya berubah sedikit, dari 11 menjadi 12,5. Namun, semua ukuran penyebaran lainnya berubah secara dramatis.

Hal ini menunjukkan bahwa rentang antarkuartil tidak dipengaruhi oleh outlier seperti ukuran dispersi lainnya. Oleh karena itu, ini adalah cara yang andal untuk mengukur distribusi 50% nilai tengah dalam distribusi apa pun.

Bacaan lebih lanjut:

Pengukuran dispersi
Kalkulator Rentang Interkuartil