Pemasangan kurva dengan python (dengan contoh)

Seringkali Anda mungkin ingin menyesuaikan kurva ke kumpulan data dengan Python.

Contoh langkah demi langkah berikut menjelaskan cara menyesuaikan kurva ke data dengan Python menggunakan fungsi numpy.polyfit() dan cara menentukan kurva mana yang paling sesuai dengan data.

Langkah 1: Buat dan visualisasikan data

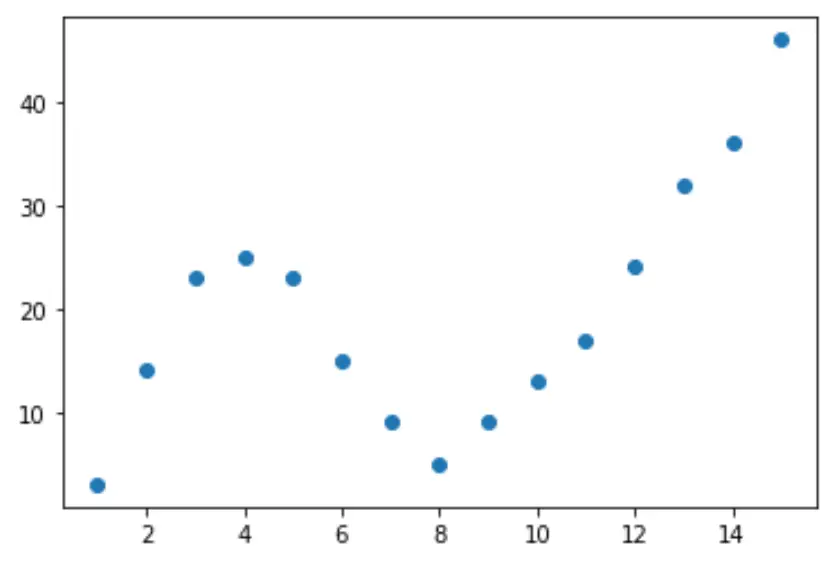
Mari kita mulai dengan membuat kumpulan data palsu, lalu membuat plot sebar untuk memvisualisasikan datanya:

 import pandas as pd
import matplotlib. pyplot as plt

#createDataFrame
df = pd. DataFrame ({' x ': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15],
                   ' y ': [3, 14, 23, 25, 23, 15, 9, 5, 9, 13, 17, 24, 32, 36, 46]})

#create scatterplot of x vs. y
plt. scatter (df. x , df. y ) 

Langkah 2: Sesuaikan Beberapa Kurva

Mari kita masukkan beberapa model regresi polinomial ke data dan visualisasikan kurva setiap model dalam plot yang sama:

 import numpy as np

#fit polynomial models up to degree 5
model1 = np. poly1d (np. polyfit (df. x , df. y , 1))
model2 = np. poly1d (np. polyfit (df. x , df. y , 2))
model3 = np. poly1d (np. polyfit (df. x , df. y , 3))
model4 = np. poly1d (np. polyfit (df. x , df. y , 4))
model5 = np. poly1d (np. polyfit (df. x , df. y , 5))

#create scatterplot
polyline = np. linspace (1, 15, 50)
plt. scatter (df. x , df. y )

#add fitted polynomial lines to scatterplot 
plt. plot (polyline, model1(polyline), color=' green ')
plt. plot (polyline, model2(polyline), color=' red ')
plt. plot (polyline, model3(polyline), color=' purple ')
plt. plot (polyline, model4(polyline), color=' blue ')
plt. plot (polyline, model5(polyline), color=' orange ')
plt. show ()

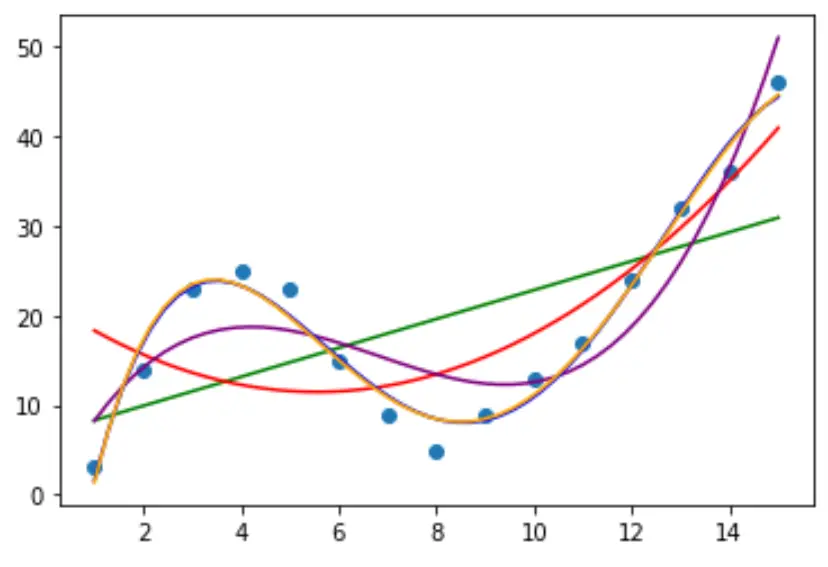
Untuk menentukan kurva mana yang paling sesuai dengan data, kita dapat melihat R kuadrat yang disesuaikan dari setiap model.

Nilai ini menunjukkan persentase variasi variabel respon yang dapat dijelaskan oleh variabel prediktor dalam model, disesuaikan dengan jumlah variabel prediktor.

 #define function to calculate adjusted r-squared
def adjR(x, y, degree):
    results = {}
    coeffs = np. polyfit (x, y, degree)
    p = np. poly1d (coeffs)
    yhat = p(x)
    ybar = np. sum (y)/len(y)
    ssreg = np. sum ((yhat-ybar)**2)
    sstot = np. sum ((y - ybar)**2)
    results[' r_squared '] = 1- (((1-(ssreg/sstot))*(len(y)-1))/(len(y)-degree-1))

    return results

#calculated adjusted R-squared of each model
adjR(df. x , df. y , 1)
adjR(df. x , df. y , 2)
adjR(df. x , df. y , 3)
adjR(df. x , df. y , 4)
adjR(df. x , df. y , 5)

{'r_squared': 0.3144819}
{'r_squared': 0.5186706}
{'r_squared': 0.7842864}
{'r_squared': 0.9590276}
{'r_squared': 0.9549709}

Dari hasil tersebut terlihat bahwa model dengan Adjusted R-squared tertinggi adalah polinomial derajat keempat yang memiliki Adjusted R-squared sebesar 0,959 .

Langkah 3: Visualisasikan kurva terakhir

Terakhir, kita dapat membuat plot sebar dengan kurva model polinomial derajat keempat:

 #fit fourth-degree polynomial
model4 = np. poly1d (np. polyfit (df. x , df. y , 4))

#define scatterplot
polyline = np. linspace (1, 15, 50)
plt. scatter (df. x , df. y )

#add fitted polynomial curve to scatterplot
plt. plot (polyline, model4(polyline), ' -- ', color=' red ')
plt. show ()

Kita juga bisa mendapatkan persamaan untuk garis ini menggunakan fungsi print() :

 print (model4)

          4 3 2
-0.01924x + 0.7081x - 8.365x + 35.82x - 26.52

Persamaan kurvanya adalah sebagai berikut:

kamu = -0,01924x ⁴ + 0,7081x ³ – 8,365x ² + 35,82x – 26,52

Persamaan ini dapat kita gunakan untuk memprediksi nilai variabel respon berdasarkan variabel prediktor dalam model. Misalnya jika x = 4 maka kita prediksi y = 23,32 :

y = -0,0192(4) ⁴ + 0,7081(4) ³ – 8,365(4) ² + 35,82(4) – 26,52 = 23,32

Sumber daya tambahan

Pengantar Regresi Polinomial
Cara melakukan regresi polinomial dengan Python