Pengujian hipotesis untuk varians

Oleh Benjamin anderson Agustus 3, 2023 Statistik 0 Komentar

Artikel ini menjelaskan apa itu pengujian hipotesis untuk varians. Jadi, Anda akan menemukan rumus untuk pengujian hipotesis varians dan, sebagai tambahan, latihan yang diselesaikan langkah demi langkah.

Apa yang dimaksud dengan pengujian hipotesis untuk varians?

Pengujian hipotesis untuk varians adalah metode statistik yang digunakan untuk menentukan ditolak atau tidaknya hipotesis nol suatu varians populasi. Dengan kata lain, pengujian hipotesis varians digunakan untuk menolak atau menerima hipotesis tentang nilai varians suatu populasi.

Secara khusus, bergantung pada nilai statistik uji hipotesis untuk varians dan tingkat signifikansi yang dipilih, hipotesis nol ditolak atau diterima.

Ingatlah bahwa pengujian hipotesis mempunyai banyak nama, bisa juga disebut kontras hipotesis, pengujian hipotesis, atau pengujian signifikansi.

Rumus Pengujian Hipotesis Varians

Statistik uji hipotesis untuk varians sama dengan selisih antara ukuran sampel dikurangi satu kali varians sampel dan dibagi dengan nilai varians populasi yang diusulkan. Statistik uji hipotesis untuk varians mempunyai distribusi chi-kuadrat .

Dengan demikian, rumus menghitung statistik uji hipotesis varians adalah sebagai berikut:

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

Emas:

$\chi^2$

adalah statistik pengujian hipotesis untuk varians yang mempunyai distribusi chi-kuadrat.
$n$

adalah ukuran sampel.
$s^2$

adalah varians sampel.
$\sigma^2$

adalah varians populasi yang diusulkan.

Untuk menginterpretasikan hasil statistik, nilai yang diperoleh harus dibandingkan dengan nilai kritis pengujian.

Jika uji hipotesis varians adalah dua sisi, hipotesis nol ditolak jika statistik lebih besar dari nilai kritis.
$\chi_{1-\alpha/2|n-1}^2$

atau jika nilai kritisnya kurang dari

$\chi_{\alpha/2|n-1}$

.
Jika uji hipotesis untuk varians cocok dengan ekor kanan, hipotesis nol ditolak jika statistik lebih besar dari nilai kritis
$\chi_{1-\alpha|n-1}^2$

.
Jika uji hipotesis untuk varians cocok dengan ekor kiri, hipotesis nol ditolak jika statistiknya kurang dari nilai kritis
$\chi_{\alpha|n-1}$

.

$\begin{array}{l}H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha/2|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si }\chi^2<\chi^2_{\alpha/2|n-1}\text{ se rechaza } H_0 \\[3ex]H_1: \sigma^2> \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2< \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2<\chi^2_{\alpha|n-1}\text{ se rechaza } H_0\end{array}$

Nilai uji hipotesis kritis varians diperoleh dari tabel distribusi chi-kuadrat. Perhatikan bahwa derajat kebebasan distribusi Chi-kuadrat adalah ukuran sampel dikurangi 1.

Contoh Pengujian Hipotesis untuk Varians di Dunia Nyata

Setelah melihat pengertian pengujian hipotesis varians dan apa rumusnya, kita akan melihat contoh konkrit untuk menyelesaikan asimilasi konsep tersebut.

Sebuah pabrik mempunyai mesin yang memproduksi suku cadang mobil dengan presisi tinggi. Namun diduga telah menjauh dan kini memproduksi suku cadang dengan celah lebih dari 8 mm ² . Untuk membantah hipotesis tersebut, dianalisis sampel sebanyak 25 buah dan varians sampelnya adalah 9,1 mm ² . Apakah hipotesis awal dapat ditolak dengan tingkat signifikansi α=0,05?

Hipotesis nol dan hipotesis alternatif untuk uji hipotesis varians ini adalah sebagai berikut:

$\begin{cases}H_0: \sigma^2=8 \\[2ex] H_1:\sigma^2>8 \end{cases}” title=”Rendered by QuickLaTeX.com” height=”65″ width=”101″ style=”vertical-align: 0px;”> Untuk menentukan apakah hipotesis nol dapat ditolak atau tidak, kita menghitung statistik uji hipotesis untuk varians menggunakan rumus yang kita lihat di atas: <p class=$ $\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

$\chi^2=\cfrac{(25-1)\cdot 9,1}{8}$

$\chi^2=27,3$

Sekarang kita mencari nilai kritis yang berhubungan dengan ekor kanan untuk 24 derajat kebebasan dan tingkat signifikansi α=0,05 pada tabel distribusi Chi-kuadrat:

$\begin{array}{c}\chi^2_{1-\alpha|n-1}=\ \color{orange}\bm{?}\color{black}\\[2ex]\chi^2_{0,95|24}=36,415\end{array}$

Dengan demikian, statistik yang dihitung lebih kecil dari nilai kritis pengujian dan oleh karena itu hipotesis nol dari pengujian hipotesis varians tidak ditolak, melainkan hipotesis alternatifnya ditolak.

$27,3<36,415 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{No se rechaza } H_0$

➤ Lihat: Pengujian hipotesis untuk mean populasi
➤ Lihat: Pengujian hipotesis untuk proporsi populasi

Pengujian hipotesis untuk varians dua populasi

Pengujian hipotesis varians dua populasi digunakan untuk menolak atau menerima hipotesis bahwa varians dari dua populasi yang berbeda adalah sama.

Jadi hipotesis nol dari uji hipotesis varians dua populasi selalu sebagai berikut:

$H_0: \sigma^2_1=\sigma^2_2$

Dan hipotesis alternatif dapat berupa salah satu dari tiga pilihan:

$\begin{array}{l}H_1:\sigma^2_1\neq \sigma^2_2\\[2ex]H_1:\sigma^2_1>\sigma^2_2\\[2ex]H_1:\sigma^2_1<\sigma^2_2\end{array}$

Dalam hal ini rumus menghitung statistik uji hipotesis varian dua populasi adalah:

$F=\cfrac{s_1^2}{s_2^2}$

Emas:

$F$

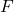
adalah statistik pengujian hipotesis untuk varian dua populasi yang mengikuti distribusi F.
$\sigma_1^2$

adalah varian populasi 1.
$\sigma_2^2$

adalah varians populasi 2.
$s_1^2$

adalah varians sampel 1.
$s_2^2$

adalah varians sampel 2.
$n_1$

adalah ukuran sampel 1.
$n_2$

adalah ukuran sampel 2.

Karena distribusi Snedecor F tidak simetris, hipotesis nol ditolak berdasarkan kriteria berikut:

[lateks]\begin{array}{l}H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } F>F_{ 1-\alpha/2|n_1-1|n_2-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow }\color{hitam} \ \text{Jika }F \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{If } F>F_{1-\alpha|n_1-1|n_2-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma_1^2< \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{hitam} \ \text{Si } F

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya