Tiga asumsi pengukuran berulang anova

ANOVA pengukuran berulang digunakan untuk menentukan apakah terdapat perbedaan yang signifikan secara statistik antara rata-rata tiga kelompok atau lebih di mana subjek yang sama muncul di setiap kelompok.

Namun, sebelum melakukan tindakan ANOVA berulang, kita harus memastikan bahwa asumsi berikut terpenuhi:

1. Independensi: Setiap observasi harus independen.

2. Normalitas : Sebaran variabel respon berdistribusi normal.

3. Kebulatan: Varians perbedaan antara semua kombinasi kelompok yang berkerabat harus sama.

Jika satu atau lebih asumsi ini dilanggar, hasil pengukuran ANOVA yang diulang mungkin tidak dapat diandalkan.

Pada artikel ini kami memberikan penjelasan untuk setiap asumsi, cara menentukan apakah asumsi tersebut terpenuhi, dan apa yang harus dilakukan jika tidak terpenuhi.

Hipotesis 1: Kemandirian

Pengukuran ANOVA berulang mengasumsikan bahwa setiap observasi dalam kumpulan data Anda tidak bergantung pada semua observasi lainnya.

Bagaimana menentukan apakah asumsi ini terpenuhi

Cara paling sederhana untuk memverifikasi asumsi ini adalah dengan memverifikasi bahwa setiap individu dalam kumpulan data diambil sampelnya secara acak dari populasi menggunakan metode random sampling .

Apabila digunakan metode random sampling, maka setiap observasi dapat diasumsikan independen.

Apa yang harus dilakukan jika asumsi ini tidak dipatuhi

Jika asumsi tersebut tidak terpenuhi maka menjadi masalah yang serius karena nilai-nilai yang dimiliki setiap individu bisa saja saling berkaitan dalam satu atau lain hal.

Seringkali satu-satunya solusi dalam skenario ini adalah merekrut individu untuk penelitian baru dengan menggunakan metode pengambilan sampel acak.

Hipotesis 2: normalitas

Pengukuran ANOVA berulang mengasumsikan bahwa sebaran variabel respon terdistribusi normal .

Bagaimana menentukan apakah asumsi ini terpenuhi

Ada dua cara untuk memeriksa apakah hipotesis ini benar:

1. Buat histogram atau plot QQ

Anda dapat memeriksa secara visual apakah distribusi variabel respons terdistribusi secara normal dengan membuat plot histogram atau QQ.

Jika Anda membuat histogram , cukup periksa apakah distribusi variabel respons kira-kira mengikuti bentuk “lonceng”. Jika demikian, Anda sering kali berasumsi bahwa asumsi normalitas terpenuhi:

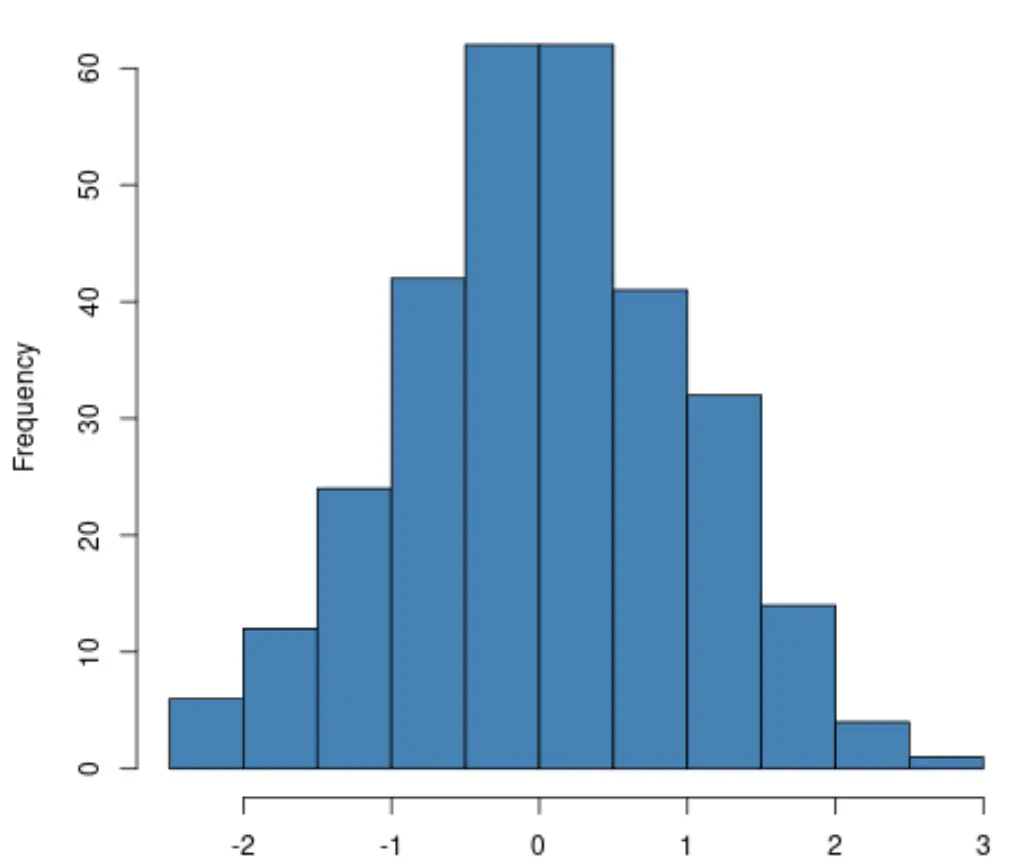
Jika Anda membuat plot QQ , periksa apakah titik data terletak di sepanjang garis diagonal lurus. Jika ya, secara umum Anda dapat berasumsi bahwa asumsi normalitas terpenuhi:

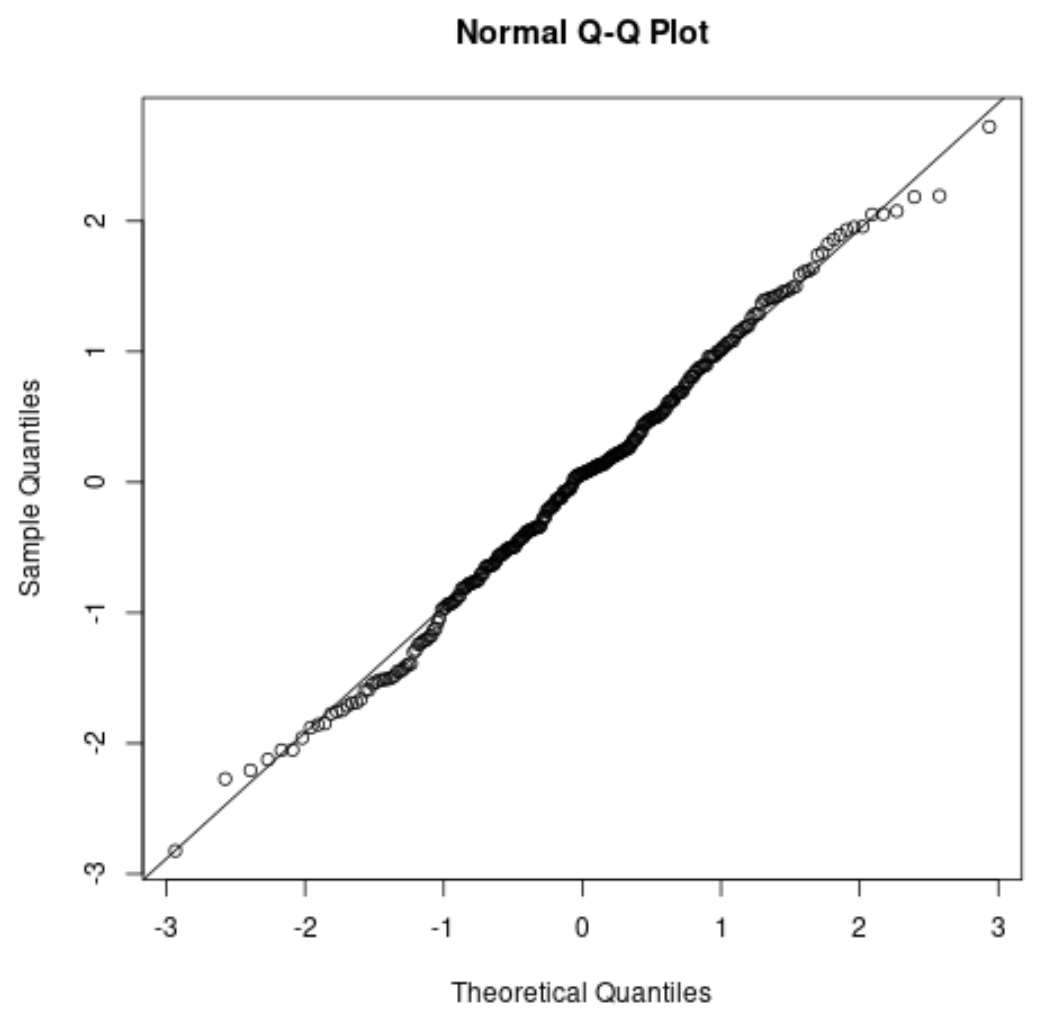
Terkait: Cara Menggunakan Plot QQ untuk Memeriksa Normalitas

2. Lakukan uji statistik formal

Anda juga dapat melakukan tes Shapiro-Wilk untuk memeriksa normalitas. Jika p-value uji tersebut kurang dari 0,05 maka hal ini menunjukkan bahwa data tidak terdistribusi normal.

Namun, perlu diketahui bahwa saat menangani sampel yang sangat besar, uji statistik seperti uji Shapiro-Wilk hampir selalu memberi tahu Anda bahwa data Anda tidak normal.

Oleh karena itu, sebaiknya periksa data Anda secara visual menggunakan bagan seperti histogram dan plot QQ. Dengan hanya melihat grafik saja anda sudah bisa mendapatkan gambaran yang cukup baik apakah datanya terdistribusi normal atau tidak.

Apa yang harus dilakukan jika asumsi ini tidak dipatuhi

Secara umum, pengukuran ulang ANOVA dianggap cukup kuat terhadap pelanggaran asumsi normalitas selama ukuran sampelnya cukup besar.

Jika asumsi normalitas dilanggar secara serius, Anda mempunyai dua pilihan:

1. Transformasikan nilai respon data Anda agar distribusinya lebih terdistribusi secara normal.

2. Melakukan uji nonparametrik yang setara seperti uji Friedman yang tidak memerlukan asumsi normalitas.

Asumsi 3: Kebulatan

ANOVA pengukuran berulang mengasumsikan kebulatan – yaitu, varians perbedaan antara semua kombinasi kelompok terkait harus sama.

Jika asumsi ini tidak terpenuhi, rasio F menjadi meningkat dan hasil pengukuran ANOVA yang berulang menjadi tidak dapat diandalkan.

Bagaimana menentukan apakah asumsi ini terpenuhi

Untuk menguji apakah asumsi ini terpenuhi, kita dapat melakukan uji kebulatan Mauchly.

Pengujian ini menggunakan hipotesis nol dan alternatif berikut:

• H ₀ : Varians selisihnya sama
• H _A : Variansi perbedaannya tidak sama

Jika p-value pengujian berada di bawah tingkat signifikansi tertentu (misalnya α = 0,05), maka kita menolak hipotesis nol dan menyimpulkan bahwa varians perbedaannya tidak sama.

Sebaliknya, jika nilai p tidak kurang dari tingkat signifikansi tertentu (misalnya α = 0,05), kita gagal menolak hipotesis nol dan menyimpulkan bahwa asumsi kebulatan terpenuhi.

Tergantung pada software statistik yang Anda gunakan, hasil tes ini akan terlihat seperti ini:

Karena nilai p tidak kurang dari 0,05, kita akan gagal menolak hipotesis nol dan menyimpulkan bahwa asumsi kebulatan terpenuhi dalam contoh khusus ini.

Apa yang harus dilakukan jika asumsi ini tidak dipatuhi

Jika kita menolak hipotesis nol uji kebulatan Mauchly, kita biasanya menerapkan koreksi pada derajat kebebasan yang digunakan untuk menghitung nilai F dalam tabel ANOVA pengukuran berulang.

Ada tiga perbaikan yang bisa kami terapkan:

• Huynh-Feldt (paling tidak konservatif)
• Serre–Geisser
• Batas bawah (paling konservatif)

Masing-masing koreksi ini cenderung meningkatkan nilai p dalam tabel keluaran ANOVA pengukuran berulang untuk memperhitungkan fakta bahwa asumsi kebulatan dilanggar.

Kita kemudian dapat menggunakan nilai p ini untuk menentukan apakah kita harus menolak hipotesis nol dari pengukuran berulang ANOVA atau tidak.

Sumber daya tambahan

Tutorial berikut memberikan informasi tambahan tentang pengukuran berulang ANOVA:

Pengantar ANOVA Tindakan Berulang
Kalkulator ANOVA Pengukuran Berulang
Cara melaporkan hasil pengukuran ANOVA yang diulang
ANOVA satu arah dan ANOVA tindakan berulang: perbedaannya