Mengapa modus penting dalam statistik?

Modus mewakili nilai yang paling sering muncul dalam kumpulan data.

Suatu kumpulan data tidak boleh memiliki mode (jika tidak ada nilai yang berulang), satu mode, atau beberapa mode.

Misalnya, mode pada dataset berikut adalah 19:

Kumpulan data: 3, 4, 11, 15, 19 , 19, 19 , 22 , 22, 23, 23, 26

Nilai inilah yang paling sering muncul.

Dalam statistik, modus penting karena alasan berikut:

Alasan 1 : Hal ini memungkinkan kita mengetahui nilai mana dalam kumpulan data yang paling umum.

Alasan 2 : Berguna untuk menemukan nilai paling sering dalam data kategorikal ketika mean dan median tidak dapat dihitung.

Alasan 3 : Ini memberi kita gambaran tentang di mana “pusat” kumpulan data berada, meskipun median dan mean lebih umum digunakan (seperti yang akan kita lihat nanti di artikel ini).

Contoh berikut menggambarkan masing-masing alasan ini dalam praktiknya.

Alasan 1: Mode memberi tahu kita nilai mana yang paling umum

Katakanlah kita memiliki kumpulan data 100.000 baris yang berisi harga jual rumah di Amerika Serikat:

Misalkan kita menggunakan perangkat lunak statistik (seperti Excel , R , Python , dll.) untuk menghitung mode kumpulan data ini dan menemukan bahwa ada tiga mode:

• $280.000
• $300.000
• $305.000

Ini segera memberi kita gambaran tentang harga rumah paling umum di kumpulan data.

Menghitung modus ribuan juga jauh lebih cepat dibandingkan melihat deretan data dan mencoba mengidentifikasi harga rumah mana yang paling sering terjadi.

Alasan 2: Mode mencari nilai paling umum dalam data kategorikal

Misalkan kita memiliki kumpulan data 1.000 baris yang memberi tahu kita warna mobil yang dimiliki oleh individu di lingkungan tertentu:

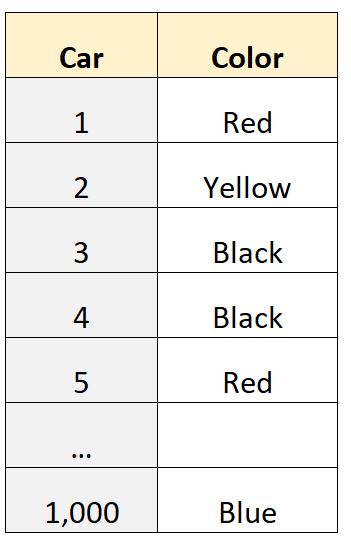
Variabel “warna” merupakan variabel kategorikal , artinya nilai-nilai tersebut termasuk dalam kategori (“merah”, “kuning”, “hitam”, dll) dan oleh karena itu kita tidak dapat menghitung nilai kuantitatif seperti rata-rata atau median. .

Namun, kita dapat menghitung modusnya karena modus tersebut hanya mewakili nilai paling umum dalam kumpulan data.

Misalnya, kita dapat menggunakan perangkat lunak statistik untuk menentukan bahwa mode kumpulan data ini adalah “hitam”, yang memberi tahu kita bahwa warna mobil yang paling umum dalam kumpulan data ini adalah hitam.

Alasan keempat: Mode memberi kita gambaran tentang di mana pusat kumpulan data berada

Modus juga dianggap sebagai ukuran tendensi sentral , artinya dapat memberi kita gambaran di mana “pusat” kumpulan data berada.

Misalnya, kita memiliki kumpulan data berikut yang memperlihatkan nilai ujian 20 siswa berbeda dalam satu kelas:

Modusnya ternyata 82 – ini adalah nilai ujian yang paling umum. Hal ini juga menjadi indikasi yang baik mengenai letak nilai skor ulasan “inti” dalam kumpulan data ini.

Namun, misalkan kita memiliki kumpulan data hasil ujian berikut:

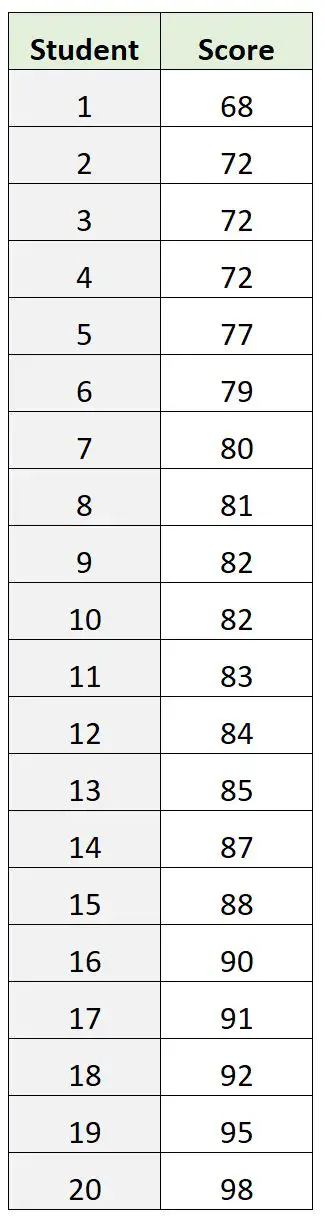
Dalam kumpulan data ini, 72 adalah nilai ujian mode. Namun, hal ini ternyata merupakan indikasi buruk mengenai di mana letak nilai “inti” ujian tersebut.

Nilai ujian rata-rata adalah 82,9 dan nilai median ujian adalah 82,5 , keduanya memberi kita gambaran yang lebih baik tentang di mana letak nilai “pusat” dalam kaitannya dengan mode.

Ringkasan

Berikut adalah ringkasan singkat dari poin-poin utama yang dibahas dalam artikel ini:

• Mode mewakili nilai yang paling sering muncul dalam kumpulan data.
• Mode ini memberi tahu kita nilai paling umum dalam data kategorikal ketika mean dan median tidak dapat digunakan.
• Modusnya memberi kita gambaran tentang di mana “pusat” kumpulan data berada, namun bisa menyesatkan jika dibandingkan dengan mean atau median.

Sumber daya tambahan

Tutorial berikut memberikan informasi tambahan tentang mean, median, dan modus dalam statistik:

Mengapa rata-rata penting dalam statistik?
Mengapa median penting dalam statistik?
Contoh Konkret: Menggunakan Mean, Median, dan Modus
Kapan Menggunakan Mean vs. Median: Dengan Contoh