Mengapa rata-rata penting dalam statistik?

Rata-rata suatu kumpulan data mewakili nilai rata-rata kumpulan data tersebut. Ini dihitung sebagai berikut:

Rata-rata = Σx _i / n

Emas:

• Σ: Simbol yang berarti “jumlah”
• x _i : Pengamatan ke- ⁱ dalam suatu kumpulan data
• n: jumlah total observasi dalam kumpulan data

Misalnya, kita memiliki kumpulan data berikut dengan 11 observasi:

Kumpulan data: 3, 4, 4, 6, 7, 8, 12, 13, 15, 16, 17

Rata-rata kumpulan data dihitung sebagai berikut:

Rata-rata = (3+4+4+6+7+8+12+13+15+16+17) / 11 = 9,54

Dalam statistik, rata-rata penting karena alasan berikut:

1. Rata-rata memberi kita gambaran di mana “pusat” kumpulan data berada.

2. Karena cara penghitungannya, rata-rata memuat informasi dari setiap observasi dalam suatu kumpulan data.

Contoh berikut menggambarkan dua alasan ini.

Contoh: Hitung rata-rata sekumpulan data

Katakanlah kita memiliki kumpulan data yang berisi harga jual 10.000 rumah berbeda di kota tertentu.

Daripada melihat ribuan baris data mentah , kita dapat menghitung nilai rata-rata untuk memahami dengan cepat harga jual rata-rata rumah di kota tersebut.

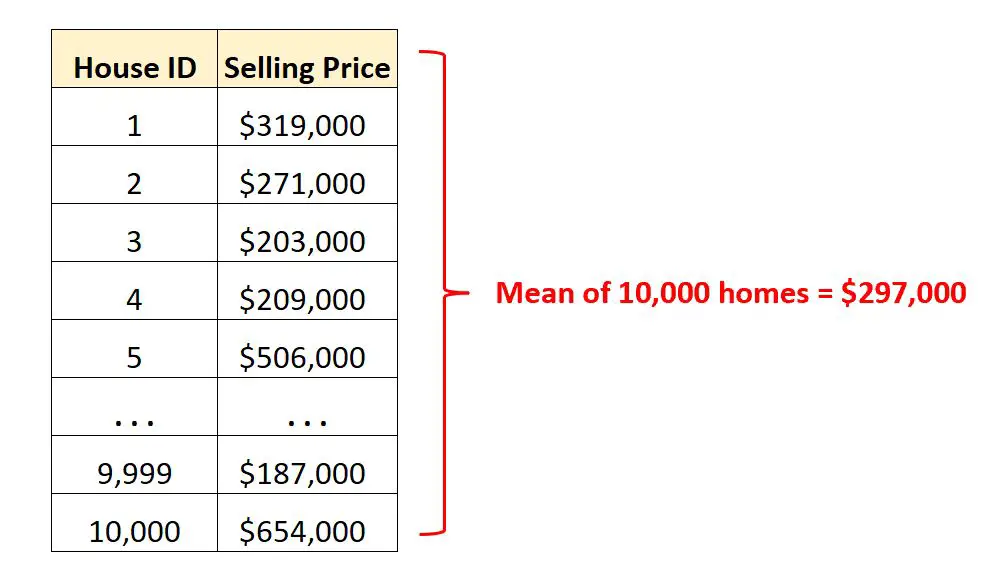
Mengetahui bahwa harga jual rata-rata adalah $297.000 memberi kita gambaran tentang berapa harga rumah “khas” di kota ini.

Nilai rata-rata tunggal ini jauh lebih mudah diinterpretasikan dibandingkan melihat seluruh baris data mentah.

Dan karena setiap harga jual rumah digunakan untuk menghitung rata-ratanya, kita dapat mengalikan harga jual rata-rata dengan jumlah total rumah untuk mencari harga jual total seluruh rumah di kota tersebut:

• Total harga jual seluruh rumah = Harga jual rata-rata * Jumlah rumah
• Total harga jual semua rumah = $297.000 * 10.000
• Total harga jual semua rumah = $2,970,000,000

Kita bisa melihat total harga jual seluruh rumah di kota ini adalah $2,97 miliar.

Kapan menggunakan rata-rata

Saat menganalisis kumpulan data, kita sering kali ingin memahami di mana letak nilai utamanya.

Dalam statistik, ada dua metrik umum yang kami gunakan untuk mengukur pusat kumpulan data:

• Mean : nilai rata-rata dalam sekumpulan data
• Median : Nilai median dalam kumpulan data

Rata-rata adalah cara paling umum untuk mengukur pusat kumpulan data, namun sebenarnya bisa menyesatkan dalam situasi berikut:

• Ketika distribusinya asimetris .
• Ketika distribusi mengandung outlier .

Untuk mengilustrasikannya, perhatikan dua contoh berikut.

Contoh 1: Menghitung mean dari distribusi yang miring

Perhatikan pembagian gaji bagi penduduk suatu kota berikut ini:

Upah yang tinggi di sisi kanan distribusi mendorong mean menjauhi pusat distribusi.

Oleh karena itu, median lebih mencerminkan gaji “tipikal” penduduk dibandingkan rata-rata, karena distribusinya condong ke kanan.

Dalam contoh khusus ini, gaji rata-rata adalah $47.000 sedangkan gaji median adalah $32.000.

Oleh karena itu, median lebih mewakili gaji rata-rata di kota tersebut.

Contoh 2: Menghitung mean jika terdapat outlier

Perhatikan grafik berikut yang menunjukkan luas rumah di suatu jalan tertentu:

Rata-rata sangat dipengaruhi oleh beberapa rumah yang sangat besar, sedangkan median tidak.

Kita dapat melihat bahwa median berfungsi lebih baik dalam menangkap luas persegi “tipikal” sebuah rumah di jalan tersebut dibandingkan rata-rata, karena tidak dipengaruhi oleh outlier.

Ringkasan

Berikut adalah ringkasan singkat dari kesimpulan utama dari artikel ini:

• Mean mewakili nilai rata-rata dalam sekumpulan data.
• Mean penting karena memberi kita gambaran di mana letak nilai sentral dalam suatu kumpulan data.
• Mean juga penting karena memuat informasi dari setiap observasi dalam suatu kumpulan data.
• Rata-rata dapat menyesatkan jika kumpulan data tidak tepat atau mengandung outlier. Dalam skenario ini, median memberikan gambaran yang lebih tepat tentang di mana “pusat” kumpulan data berada.

Sumber daya tambahan

Tutorial berikut memberikan informasi tambahan tentang statistik deskriptif lainnya:

Mengapa median penting dalam statistik?
Mengapa deviasi standar penting dalam statistik?
Kapan menggunakan mean versus median