Excel: membuat perbandingan statistik dua kumpulan data

Seringkali, Anda mungkin ingin melakukan perbandingan statistik dua kumpulan data di Excel untuk memahami perbedaan distribusi nilai di setiap kumpulan data.

Ada dua cara umum untuk melakukan perbandingan statistik:

Metode 1: Hitung ringkasan lima digit dari setiap kumpulan data

Kita dapat menghitung ringkasan lima angka dari setiap kumpulan data, yang terdiri dari nilai-nilai berikut:

• Nilai minimum
• Kuartil pertama (persentil ke-25)
• Median (persentil ke-50)
• Kuartil ketiga (persentil ke-75)
• Maksimal

Dengan menghitung kelima nilai tersebut, kita dapat memperoleh pemahaman yang baik tentang sebaran nilai pada setiap kumpulan data.

Metode 2: Hitung mean dan deviasi standar

Cara yang lebih sederhana untuk melakukan perbandingan statistik dua kumpulan data adalah dengan menghitung mean dan deviasi standar setiap kumpulan data.

Hal ini membantu kita memahami kira-kira di mana letak nilai “pusat” dan bagaimana distribusi nilai di setiap kumpulan data.

Contoh berikut menunjukkan bagaimana menggunakan masing-masing metode ini dalam praktiknya.

Contoh: Lakukan perbandingan statistik dua kumpulan data di Excel

Misalkan kita memiliki dua kumpulan data di Excel yang memperlihatkan hasil siswa dari dua kelas berbeda yang diperoleh pada ujian tertentu:

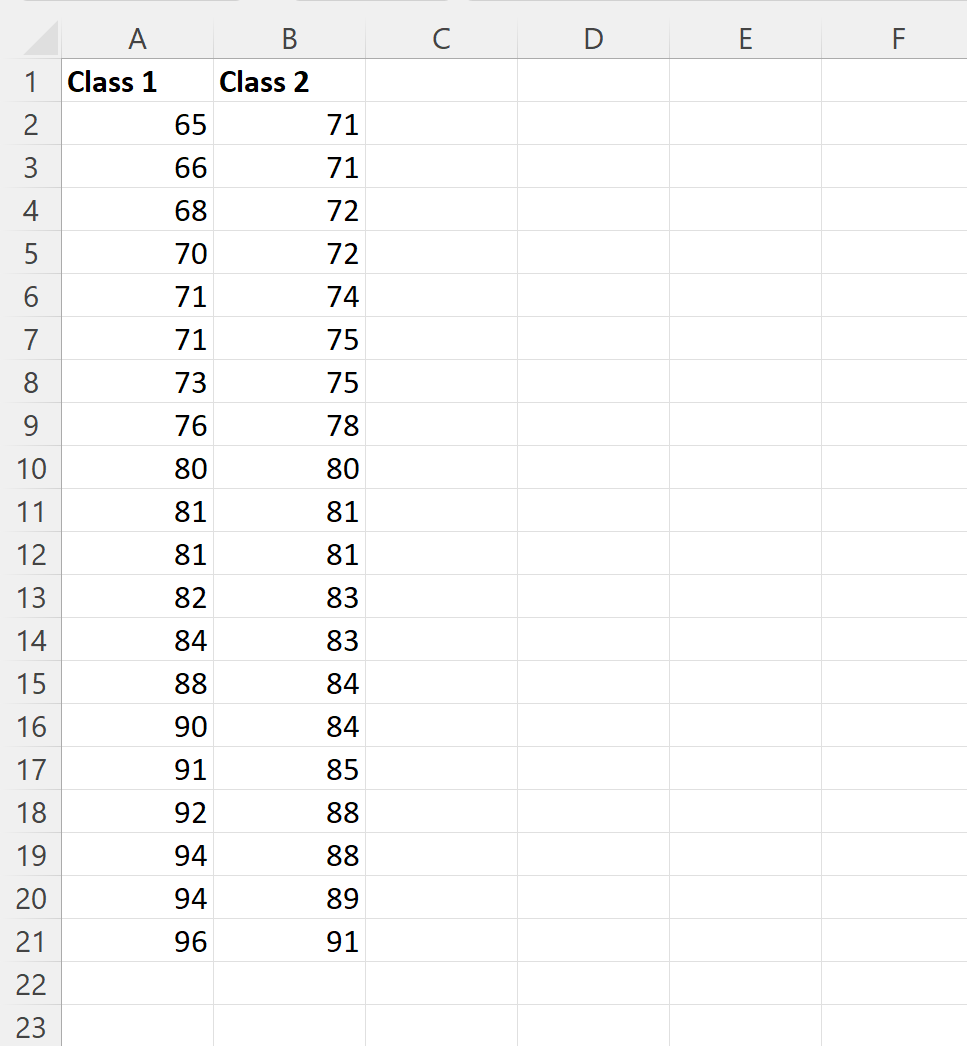
Kita dapat mengetikkan rumus berikut pada sel kolom E untuk menghitung ringkasan lima digit hasil ujian kelas 1:

• E2 : =MIN(A2:A21)
• E3 : =KUARTIL(A2:A21, 1)
• E4 : =MEDIAN(A2:A21)
• E5 : =KUARTILE(A2:A21, 3)
• E6 : =MAX(A2:A21

Kita kemudian dapat mengklik dan menyeret rumus ini ke kanan untuk menghitung nilai yang sama untuk kelas 2:

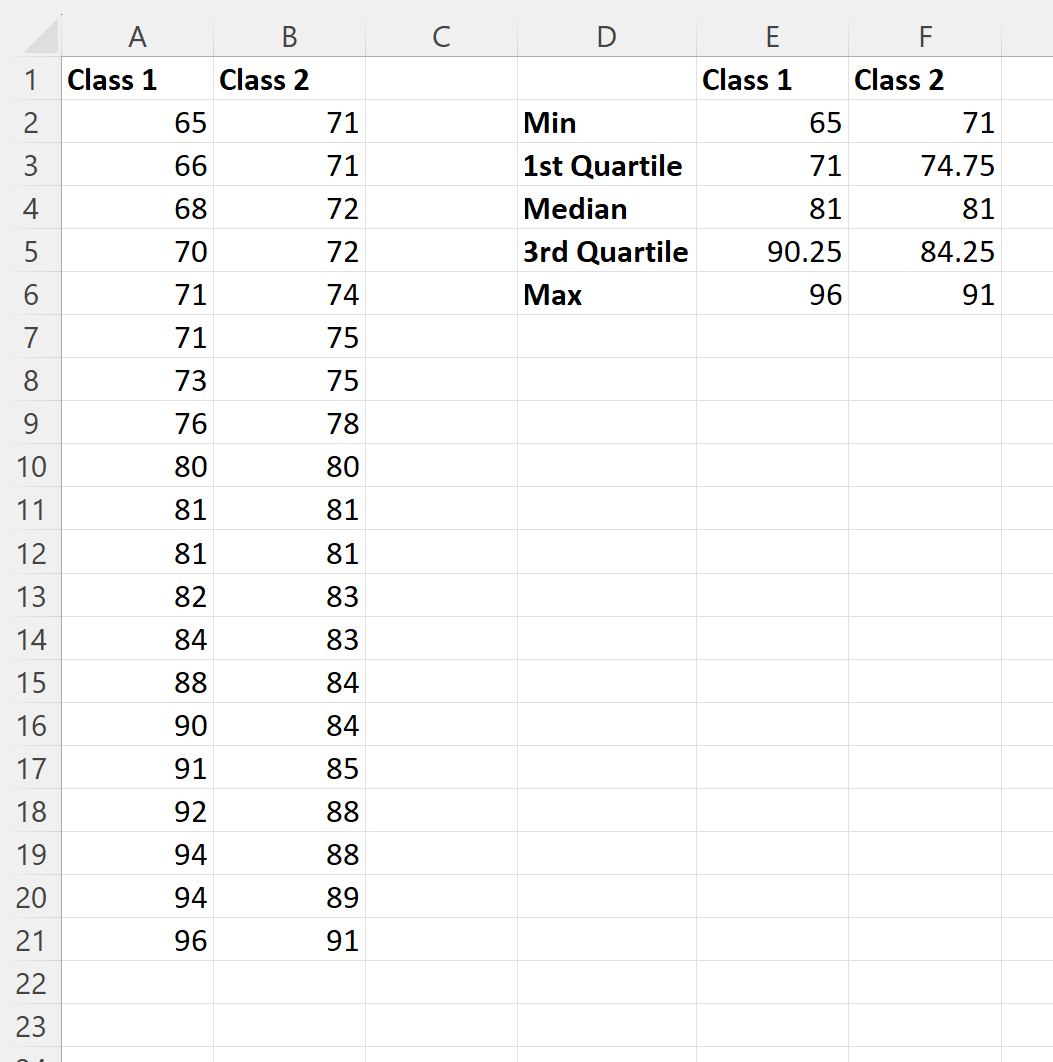
Kita kemudian dapat memasukkan rumus berikut ke dalam sel kolom E untuk menghitung mean dan deviasi standar hasil ujian Kelas 1:

• E8 : =RATA-RATA(A2:A21)
• E9 : =ETDEV(A2:A21, 1)

Kita kemudian dapat mengklik dan menyeret rumus ini ke kanan untuk menghitung nilai yang sama untuk kelas 2:

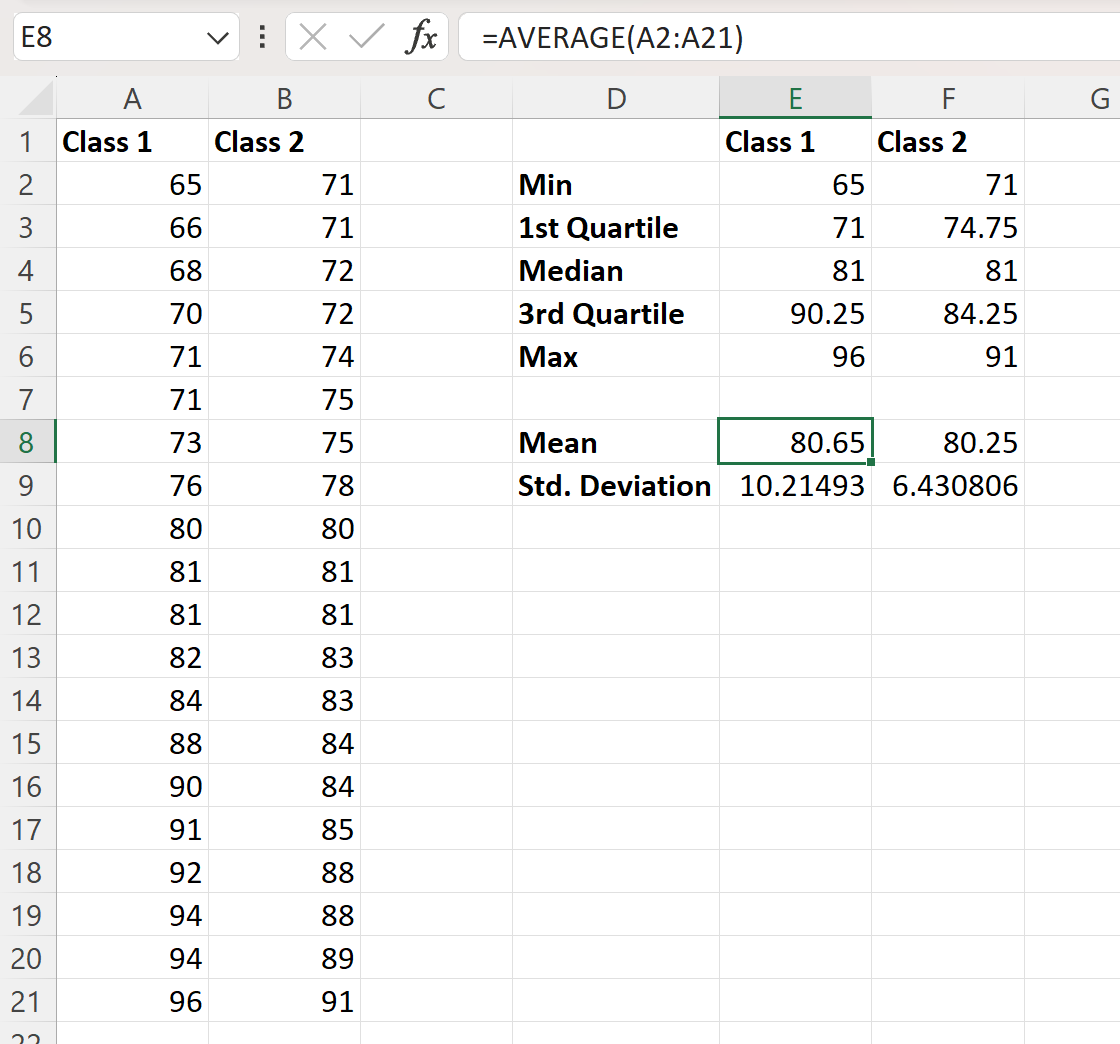
Kita dapat menarik kesimpulan berikut dari perbandingan statistik kedua kumpulan data ini:

Kesimpulan 1: Kedua kumpulan data memiliki nilai “inti” yang serupa.

Kedua dataset tersebut memiliki median nilai ujian sebesar 81. Nilai rata-ratanya hanya berbeda sedikit: kelas pertama memiliki rata-rata nilai ujian sebesar 80,65 sedangkan kelas kedua memiliki rata-rata nilai ujian sebesar 80,65 sedangkan kelas kedua memiliki rata-rata nilai ujian sebesar 80,65. 80,65′ ulasan 80,25.

Hal ini menunjukkan bahwa nilai ujian “inti” atau “tipikal” antara kedua kelas adalah serupa.

Kesimpulan 2: Kumpulan data pertama memiliki “sebaran” nilai yang jauh lebih besar.

Beberapa indikator menunjukkan bahwa hasil ujian kelas satu jauh lebih tersebar dibandingkan hasil ujian kelas kedua.

Misalnya, cakupan kelas 1 jauh lebih tinggi:

• Kisaran kelas 1: 96 – 65 = 31
• Kisaran kelas 2: 91 – 71 = 20

Kisaran interkuartil kelas 1 juga jauh lebih tinggi:

• Rentang interkuartil kelas 1: 90,25 – 71 = 19,25
• Rentang interkuartil kelas 2: 84,25 – 74,75 = 9,5

Standar deviasi kelas 1 juga jauh lebih tinggi:

• Simpangan baku kelas 1: 10.21
• Standar deviasi kelas 2 : 6,43

Masing-masing ukuran ini menunjukkan kepada kita bahwa kesenjangan nilai ujian siswa Kelas 1 jauh lebih tinggi dibandingkan kesenjangan nilai ujian siswa Kelas 2.

Sumber daya tambahan

Tutorial berikut menjelaskan cara melakukan operasi umum lainnya di Excel:

Cara Membuat Tabel Ringkasan di Excel
Cara menghitung median berdasarkan grup di Excel
Cara Menghitung Deviasi Standar dan Mengabaikan Nol di Excel