Perbedaan

Oleh Benjamin anderson Agustus 5, 2023 Statistik 0 Komentar

Pada artikel ini kami menjelaskan apa itu varians, disebut juga varians, dan cara menghitungnya. Anda akan menemukan rumus varians, contoh nyata penghitungan varians, dan sebagai tambahan, Anda akan dapat menghitung varians kumpulan data apa pun dengan kalkulator online.

Kami juga menunjukkan cara mencari varians data yang dikelompokkan, karena ini dilakukan dengan cara yang berbeda. Terakhir, kami akan mengajari Anda perbedaan antara varians populasi dan varians sampel, perbedaan antara varians dan deviasi standar, serta sifat-sifat ukuran statistik ini.

Apa itu varians?

Dalam statistik, varians adalah ukuran penyebaran yang menunjukkan variabilitas suatu variabel acak. Variansnya sama dengan jumlah kuadrat residu dibagi dengan jumlah observasi.

Ingatlah bahwa residu dipahami sebagai perbedaan antara nilai suatu titik data statistik dan rata-rata kumpulan data.

Dalam teori probabilitas, simbol varians adalah huruf Yunani sigma kuadrat (σ ² ). Meskipun biasanya juga direpresentasikan sebagai Var(X) , dengan X sebagai variabel acak yang variansnya dihitung.

Secara umum, menafsirkan nilai varians suatu variabel acak itu sederhana. Semakin besar nilai variansnya maka semakin tersebar datanya. Begitu pula sebaliknya, semakin kecil nilai variansnya, maka semakin kecil pula sebaran yang ada pada seri data tersebut. Namun, ketika menafsirkan varians, kita harus berhati-hati terhadap outlier , karena dapat merusak nilai varians.

varians, ukuran lain yang dipertimbangkan selain dispersi adalah rentang, deviasi standar, deviasi rata-rata, dan koefisien variasi.

Cara menghitung kesenjangan

Untuk menghitung varians, langkah-langkah berikut harus dilakukan:

Temukan mean aritmatika dari kumpulan data.
Hitung residunya, yang didefinisikan sebagai selisih antara nilai dan rata-rata kumpulan data.
Kuadratkan setiap sisanya.
Tambahkan semua hasil yang dihitung pada langkah sebelumnya.
Bagilah dengan jumlah total data. Hasil yang diperoleh adalah varians dari seri data tersebut.

Kesimpulannya, rumus menghitung varians suatu kumpulan data adalah:

Emas:

$X$

adalah variabel acak yang ingin Anda hitung variansnya.
$x_i$

adalah nilai datanya

$i$

.
$n$

adalah jumlah total pengamatan.
$\overline{X}$

adalah mean dari variabel acak

$X$

.

👉 Anda dapat menggunakan kalkulator di bawah ini untuk menghitung varians kumpulan data apa pun.

Oleh karena itu, untuk mengekstrak varians dari suatu rangkaian data, penting bagi Anda untuk mengetahui cara menghitung rata-rata aritmatika. Jika Anda tidak ingat cara melakukannya, Anda dapat memeriksanya di artikel yang ditautkan di atas.

Contoh penyimpangan

Sekarang setelah kita mengetahui definisi varians, kita akan menyelesaikan latihan langkah demi langkah sehingga Anda dapat melihat bagaimana varians suatu rangkaian data diperoleh.

Dari sebuah perusahaan multinasional diketahui hasil ekonomi yang diperolehnya dalam lima tahun terakhir, sebagian besar memperoleh keuntungan namun dalam satu tahun menimbulkan kerugian yang cukup besar: 11.5, 2, -9, 7 juta euro. Hitung varians kumpulan data ini.

Seperti yang kita lihat pada penjelasan di atas, hal pertama yang perlu kita lakukan untuk mencari varians suatu deret data adalah dengan menghitung mean aritmatikanya:

$\overline{X}=\cfrac{11+5+2+(-9)+7}{5}=3,2$

Dan setelah kita mengetahui nilai rata-rata datanya, kita dapat menggunakan rumus varians:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n}$

Kami mengganti data yang disediakan oleh pernyataan latihan ke dalam rumus:

$Var(X)=\cfrac{\displaystyle (11-3,2)^2+(5-3,2)^2+(2-3,2)^2+(-9-3,2)^2+(7-3,2)^2}{5}$

Terakhir, yang tersisa hanyalah menyelesaikan operasi penghitungan varians:

$\begin{aligned}Var(X)&=\cfrac{7,8^2+1,8^2+(-1,2)^2+(-12,2)^2+3,8^2}{5}\\[2ex]&=\cfrac{60,84+3,24+1,44+148,84+14,44}{5}\\[2ex]&= \cfrac{228,8}{5} \\[2ex]&=45,76 \ \text{millones de euros}^2\end{aligned}$

Perhatikan bahwa unit varians adalah unit yang sama dengan data statistik tetapi dikuadratkan, oleh karena itu varians kelompok data ini adalah 45,76 juta euro ² .

Kalkulator Kesenjangan

Masukkan kumpulan data statistik ke dalam kalkulator berikut untuk menghitung variansnya. Data harus dipisahkan dengan spasi dan dimasukkan menggunakan titik sebagai pemisah desimal.

Varians untuk data yang dikelompokkan

Untuk menghitung varians data yang dikelompokkan ke dalam interval , langkah-langkah berikut harus diikuti:

Temukan mean dari data yang dikelompokkan.
Hitung sisa data yang dikelompokkan.
Kuadratkan setiap sisanya.
Kalikan setiap hasil sebelumnya dengan frekuensi intervalnya.
Tambahkan jumlah semua nilai yang diperoleh pada langkah sebelumnya.
Bagilah dengan jumlah total observasi. Angka yang dihasilkan merupakan varians dari data yang dikelompokkan.

Dengan kata lain rumus menghitung varians data yang dikelompokkan ke dalam interval adalah sebagai berikut:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2\cdot f_i }{n}$

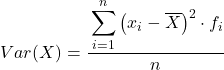
Meskipun rumus di atas biasanya digunakan, persamaan aljabar di bawah ini juga dapat digunakan karena persamaannya:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{n}-\overline{X}^2$

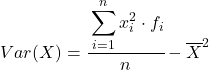
Sebagai contoh, kita akan mencari varians dari rangkaian data yang dikelompokkan berikut:

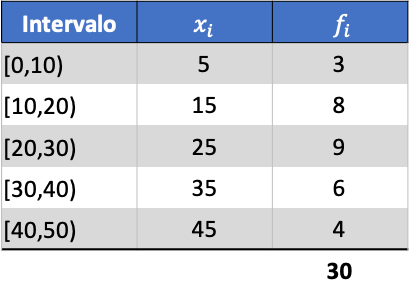
Pertama, kita perlu menentukan rata-rata data yang dikelompokkan. Untuk melakukan ini, kami menambahkan kolom di tabel frekuensi dengan produk dari nilai kelas dan frekuensi:

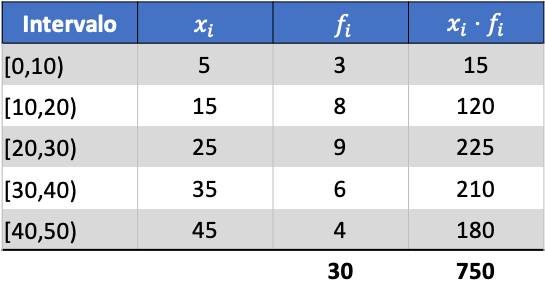
Sekarang kita menghitung rata-rata data yang dikelompokkan dengan membagi jumlah kolom yang ditambahkan dengan jumlah total data:

$\overline{X}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{n}=\cfrac{750}{30}=25$

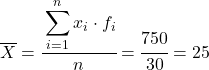
Dan dari rata-rata data yang dihitung, kita dapat menambahkan tiga kolom berikut:

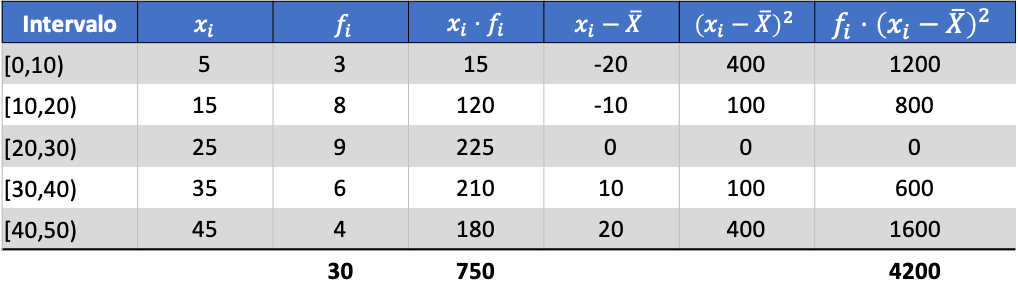
Jadi varians kumpulan data yang dikumpulkan adalah jumlah kolom terakhir dibagi dengan jumlah total data observasi:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2\cdot f_i }{n}=\cfrac{4200}{30}=140$

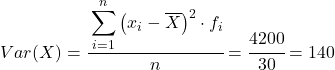
Varians dan deviasi standar

Varians dan deviasi standar (atau deviasi standar) adalah dua ukuran penyebaran dan oleh karena itu keduanya menunjukkan tingkat penyebaran kumpulan data. Namun perbedaan antara varians dan simpangan baku adalah pada umumnya varians mempunyai nilai yang lebih besar karena merupakan kuadrat dari simpangan baku.

Simpangan baku umumnya dilambangkan dengan huruf Yunani sigma (σ), dan oleh karena itu varians dilambangkan dengan huruf sigma kuadrat (σ ² ), karena ini adalah hubungan matematis yang ada antara kedua metrik dispersi ini.

$Var(X)=\sigma^2$

Jadi, setelah Anda menghitung nilai varians suatu kumpulan data, Anda dapat dengan mudah mencari nilai deviasi standar dari kumpulan data yang sama hanya dengan mengambil akar kuadrat dari varians tersebut.

$\sigma=\sqrt{\sigma^2}$

Varians populasi dan varians sampel

Logikanya, varians populasi mengacu pada penghitungan varians suatu populasi statistik dan, sebaliknya, varians sampel diterapkan pada penghitungan varians suatu sampel. Namun, ini adalah dua konsep yang berbeda karena rumus varians populasi berbeda dengan rumus varians sampel.

Biasanya dalam latihan varians, jika mereka tidak memberi tahu kita sebaliknya, untuk mencari varians dari kumpulan data yang disediakan kita harus menggunakan rumus varians populasi , yang telah kami jelaskan di awal artikel:

$\sigma^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n}$

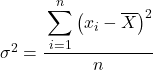
Namun mungkin dalam beberapa soal Anda diminta untuk memperlakukan data statistik sebagai sampel, dalam hal ini kita perlu menggunakan rumus varians sampel :

$s^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n-1}$

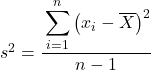
Perhatikan bahwa untuk menunjukkan bahwa varians populasi sedang dihitung, hal ini ditunjukkan dengan huruf Yunani σ, tetapi ketika varians sampel sedang dihitung, huruf s digunakan.

Seperti yang Anda lihat, satu-satunya perbedaan antara kedua rumus tersebut adalah bahwa dalam varians suatu sampel kita perlu membaginya dengan jumlah observasi dikurangi 1, misalnya jika total item data ada 30 maka kita akan membaginya dengan 29. Namun perhitungan pembilangnya dilakukan dengan cara yang persis sama.

Sifat varians

Varians mempunyai sifat sebagai berikut:

Varians dari setiap variabel acak akan selalu lebih besar atau sama dengan nol. Begitu pula jika variansnya nol, berarti semua data statistiknya sama.

$Var(x)\ge 0$

Jelasnya, varians suatu nilai adalah nol.

$Var(a)=0\qquad a\in \mathbb{R}$

Varians hasil kali skalar dengan suatu variabel setara dengan skalar kuadrat dikalikan varians variabel.

$Var(aX)=a^2\cdot Var(X)\qquad a\in \mathbb{R}$

Varians dari jumlah dua variabel dependen sama dengan jumlah varians masing-masing variabel secara terpisah ditambah dua kali kovarians antara kedua variabel.

$Var(X+Y)=Var(X)+Var(Y)+2Cov(X,Y)$

Oleh karena itu, jika kedua variabel tersebut independen, maka untuk menentukan varians dari jumlah keduanya, cukup dengan menjumlahkan variansnya:

$Var(X+Y)=Var(X)+Var(Y)$

Penyimpangan juga dapat ditentukan dengan ekspektasi matematis dengan menggunakan rumus berikut:

$Var(X)=E\bigl[(X-\overline{X})^2\bigr]$

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya