Interval kepercayaan untuk perbedaan antar rata-rata
Interval kepercayaan (CI) untuk selisih rata-rata adalah rentang nilai yang kemungkinan besar memuat perbedaan sebenarnya antara dua rata-rata populasi dengan tingkat kepercayaan tertentu.
Tutorial ini menjelaskan hal berikut:
- Motivasi untuk menciptakan interval kepercayaan ini.
- Rumus untuk membuat interval kepercayaan ini.
- Contoh cara menghitung interval kepercayaan ini.
- Bagaimana menafsirkan interval kepercayaan ini.
CI untuk perbedaan cara: motivasi
Peneliti sering kali ingin memperkirakan perbedaan rata-rata dua populasi. Untuk memperkirakan perbedaan ini, mereka akan mengumpulkan sampel acak dari setiap populasi dan menghitung mean untuk setiap sampel. Kemudian mereka dapat membandingkan perbedaan antara kedua rata-rata tersebut.
Namun, mereka tidak dapat mengetahui dengan pasti apakah perbedaan antara rata-rata sampel sesuai dengan perbedaan sebenarnya antara rata-rata populasi. Inilah sebabnya mengapa mereka dapat menciptakan interval kepercayaan untuk perbedaan antara kedua rata-rata tersebut. Hal ini memberikan rentang nilai yang mungkin mengandung perbedaan sebenarnya antara rata-rata populasi.
Misalnya, kita ingin memperkirakan perbedaan berat rata-rata antara dua spesies penyu yang berbeda. Karena terdapat ribuan penyu dalam setiap populasi, maka akan memakan waktu dan biaya yang terlalu besar untuk berkeliling dan menimbang setiap penyu satu per satu.
Sebagai gantinya, kita dapat mengambil sampel acak sederhana yang terdiri dari 15 penyu dari setiap populasi dan menggunakan berat rata-rata setiap sampel untuk memperkirakan perbedaan sebenarnya dalam berat rata-rata antara kedua populasi:
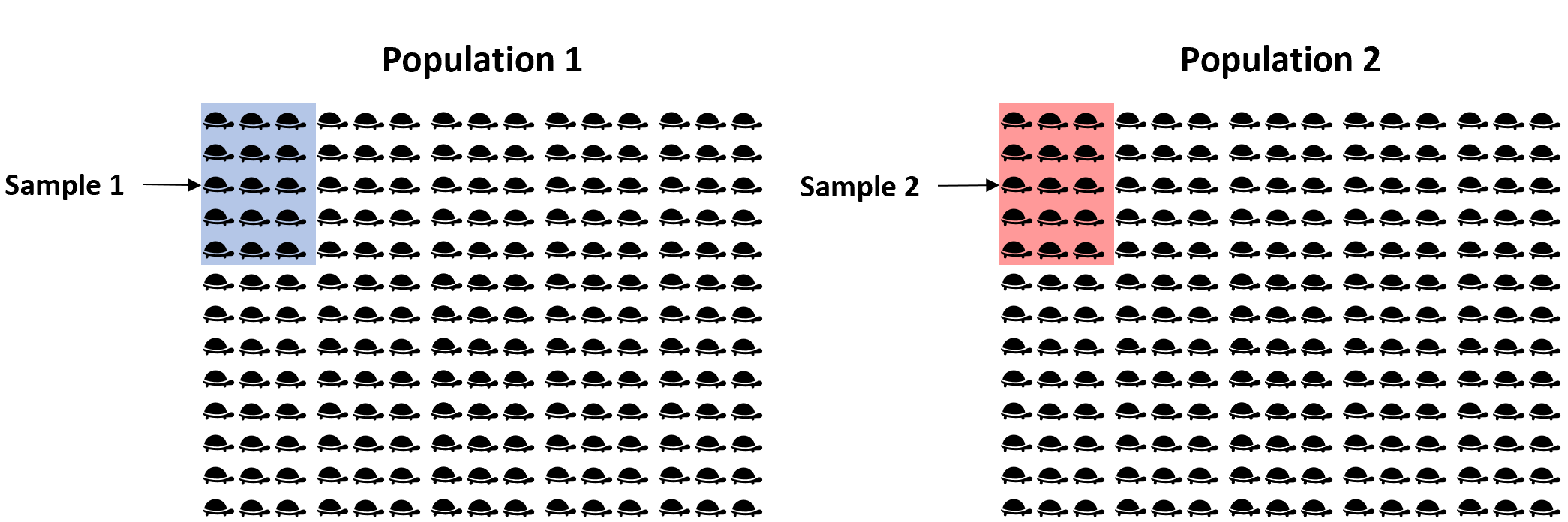
Permasalahannya adalah sampel kita bersifat acak, sehingga tidak ada jaminan bahwa perbedaan rata-rata bobot antara kedua sampel sama persis dengan perbedaan rata-rata bobot antara kedua populasi. Jadi, untuk menangkap ketidakpastian ini, kita dapat membuat interval kepercayaan yang berisi rentang nilai yang kemungkinan besar memuat perbedaan rata-rata bobot sebenarnya antara kedua populasi.
CI untuk selisih rata-rata: rumus
Kami menggunakan rumus berikut untuk menghitung interval kepercayaan untuk selisih antara dua rata-rata:
Interval kepercayaan = ( x 1 – x 2 ) +/- t*√((s p 2 /n 1 ) + (s p 2 /n 2 ))
Emas:
- x 1 , x 2 : rata-rata sampel 1, rata-rata sampel 2
- t : nilai t-kritis berdasarkan tingkat kepercayaan dan (n 1 + n 2 -2) derajat kebebasan
- s p 2 : varians gabungan
- n 1 , n 2 : ukuran sampel 1, ukuran sampel 2
Emas:
- Varians gabungan dihitung sebagai berikut: s p 2 = ((n 1 -1)s 1 2 + (n 2 -1)s 2 2 ) / (n 1 +n 2 -2)
- Nilai t-kritis t dapat dicari dengan menggunakan kalkulator distribusi t terbalik.
CI untuk perbedaan rata-rata: contoh
Misalkan kita ingin memperkirakan perbedaan berat rata-rata antara dua spesies penyu yang berbeda. Oleh karena itu kami akan mengumpulkan sampel acak sebanyak 15 penyu dari setiap populasi. Berikut ringkasan data untuk setiap sampel:
Contoh 1:
- x1 = 310
- s 1 = 18,5
- n 1 = 15
Contoh 2:
- x2 = 300
- s2 = 16,4
- n2 = 15
Berikut cara mencari interval kepercayaan yang berbeda untuk perbedaan sebenarnya dalam bobot rata-rata populasi:
Interval kepercayaan 90%:
(310-300) +/- 1,70*√((305,61/15) + (305,61/15)) = [-0,8589, 20,8589]
Interval kepercayaan 95%:
(310-300) +/- 2,05*√((305,61/15) + (305,61/15)) = [-3,0757, 23,0757]
Interval kepercayaan 99%:
(310-300) +/- 2,76*√((305,61/15) + (305,61/15)) = [-7,6389, 27,6389]
Catatan: Anda juga dapat menemukan interval kepercayaan ini menggunakan Interval Keyakinan Statistik untuk Kalkulator Perbedaan Antara Rata-rata .
Anda akan melihat bahwa semakin tinggi tingkat kepercayaan, semakin lebar interval kepercayaannya. Hal ini seharusnya masuk akal, karena interval yang lebih lebar kemungkinan besar berisi rata-rata populasi sebenarnya, sehingga kita lebih “yakin” bahwa interval tersebut berisi rata-rata populasi sebenarnya.
CI untuk perbedaan rata-rata : interpretasi
Cara kita menafsirkan interval kepercayaan adalah:
Ada kemungkinan 95% bahwa interval kepercayaan [-3.0757, 23.0757] berisi perbedaan sebenarnya dalam berat rata-rata antara kedua populasi penyu.
Karena interval ini mengandung nilai “0”, berarti kemungkinan tidak ada perbedaan rata-rata berat badan penyu dari kedua populasi tersebut. Dengan kata lain, kita tidak dapat mengatakan dengan keyakinan 95% bahwa terdapat perbedaan rata-rata berat badan penyu dari kedua populasi tersebut.