Persentil, kuartil, dan kuantil: apa bedanya?

Tiga istilah yang sering membingungkan siswa dalam statistika adalah persentil, kuartil, dan kuantil.

Berikut adalah definisi sederhana masing-masing:

Persentil: berkisar dari 0 hingga 100.

Kuartil: berkisar dari 0 hingga 4.

Kuantil: berpindah dari nilai apa pun ke nilai lainnya.

Perhatikan bahwa persentil dan kuartil hanyalah jenis kuantil.

Beberapa jenis kuantil bahkan memiliki nama tertentu, antara lain:

• Keempat kuantil tersebut disebut kuartil .
• Kelima kuantil tersebut disebut kuintil .
• 8 kuantil disebut oktil .
• Kesepuluh kuantil tersebut disebut desil .
• 100 kuantil disebut persentil .

Perhatikan bahwa persentil dan kuartil memiliki hubungan berikut:

• 0 persentil = 0 kuartil (disebut juga minimum)
• Persentil ke-25 = kuartil ke-1
• Persentil ke-50 = kuartil ke-2 (disebut juga median)
• Persentil ke-75 = kuartil ke-3
• Persentil ke-100 = kuartil ke-4 (disebut juga maksimum)

Contoh: Mencari persentil dan kuartil

Misalkan kita memiliki kumpulan data berikut dengan 20 nilai:

Dengan menggunakan perangkat lunak statistik (seperti Excel, R, Python, dll.), kita dapat menemukan persentil dan kuartil berikut untuk kumpulan data ini:

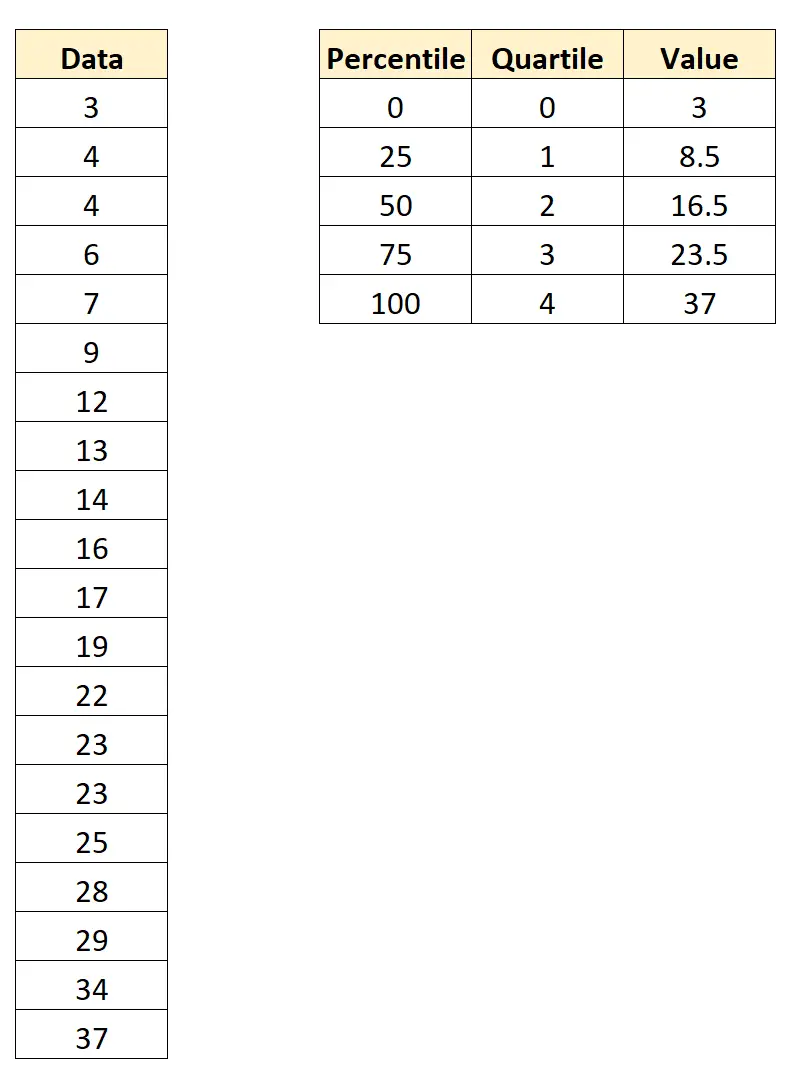
Berikut cara menafsirkan nilai-nilai ini:

• Persentil 0 dan kuartil 0 adalah 3 .
• Persentil ke-25 dan kuartil ke-1 adalah 8,5 .
• Persentil ke-50 dan kuartil ke-2 adalah 16,5 .
• Persentil ke-75 dan kuartil ke-3 adalah 23,5 .
• Persentil ke-100 dan kuartil ke-4 adalah 37 .

Kapan menggunakan persentil versus kuartil

Persentil dapat digunakan untuk menjawab pertanyaan seperti:

Berapa nilai yang dibutuhkan seorang siswa pada tes tertentu agar bisa masuk 10% teratas?

Untuk menjawab pertanyaan ini, kita akan mencari persentil ke-90 dari seluruh skor, yang merupakan nilai yang memisahkan 90% terbawah dari 10% teratas.

Berapa tinggi badan yang mencakup 40% tinggi rata-rata siswa di sekolah tertentu?

Untuk menjawab pertanyaan ini, kita akan mencari persentil tinggi ke-70 dan persentil tinggi ke-30, yang merupakan dua nilai yang menentukan batas atas dan bawah untuk 40% tinggi bagian tengah.

Kuartil dapat digunakan untuk menjawab pertanyaan seperti:

Berapa nilai yang dibutuhkan seorang siswa dalam suatu ujian agar dapat memperoleh nilai seperempat teratas?

Untuk menjawab pertanyaan ini, kita akan mencari kuartil ke-3 dari semua skor, yaitu nilai yang memisahkan 75% terbawah dan 25% teratas.

Berapa rentang interkuartil dari kumpulan data tertentu?

Rentang interkuartil (IQR) adalah kisaran 50% tengah dari nilai data. Untuk mencari IQR suatu kumpulan data tertentu, kita dapat menghitung kuartil ke-3 – kuartil ke-1.

Sumber daya tambahan

Cara menghitung persentil di R
Cara menghitung kuartil di R
Cara Menghitung Rentang Interkuartil di Excel
Cara Menghitung Rentang Interkuartil pada Kalkulator TI-84