Plot kotak dan kumis

Oleh Benjamin anderson Agustus 5, 2023 Statistik 0 Komentar

Artikel ini menjelaskan apa itu plot kotak, juga dikenal sebagai plot kotak (atau plot kotak). Anda akan menemukan bagaimana jenis diagram statistik ini dibuat dan latihan diagram kotak dan kumis serta interpretasinya.

Apa itu plot kotak dan kumis?

Boxplot , juga disebut boxplot atau boxplot , adalah grafik yang secara visual mewakili sekumpulan data statistik menggunakan kuartil.

Ciri utama plot kotak dan kumis adalah memungkinkan Anda memvisualisasikan sebaran serangkaian data dengan cepat, karena menunjukkan kuartil, median, nilai ekstrem, dan outlier data.

Jadi, diagram jenis ini terdiri dari kotak persegi panjang dan beberapa garis (atau kumis) yang darinya muncul nilai-nilai berikut:

Batas kotak menunjukkan kuartil pertama dan ketiga (Q ₁ dan Q ₃ ). Dan garis vertikal di dalam kotak adalah median (setara dengan kuartil kedua _Q2 ).
Batas kumis (atau lengan) adalah nilai ekstrim , yaitu nilai minimum dan nilai maksimum dari rangkaian data.
Titik-titik di luar garis adalah outlier , atau dengan kata lain, data yang mungkin diukur secara tidak benar sehingga tidak boleh diperhitungkan dalam studi statistik.

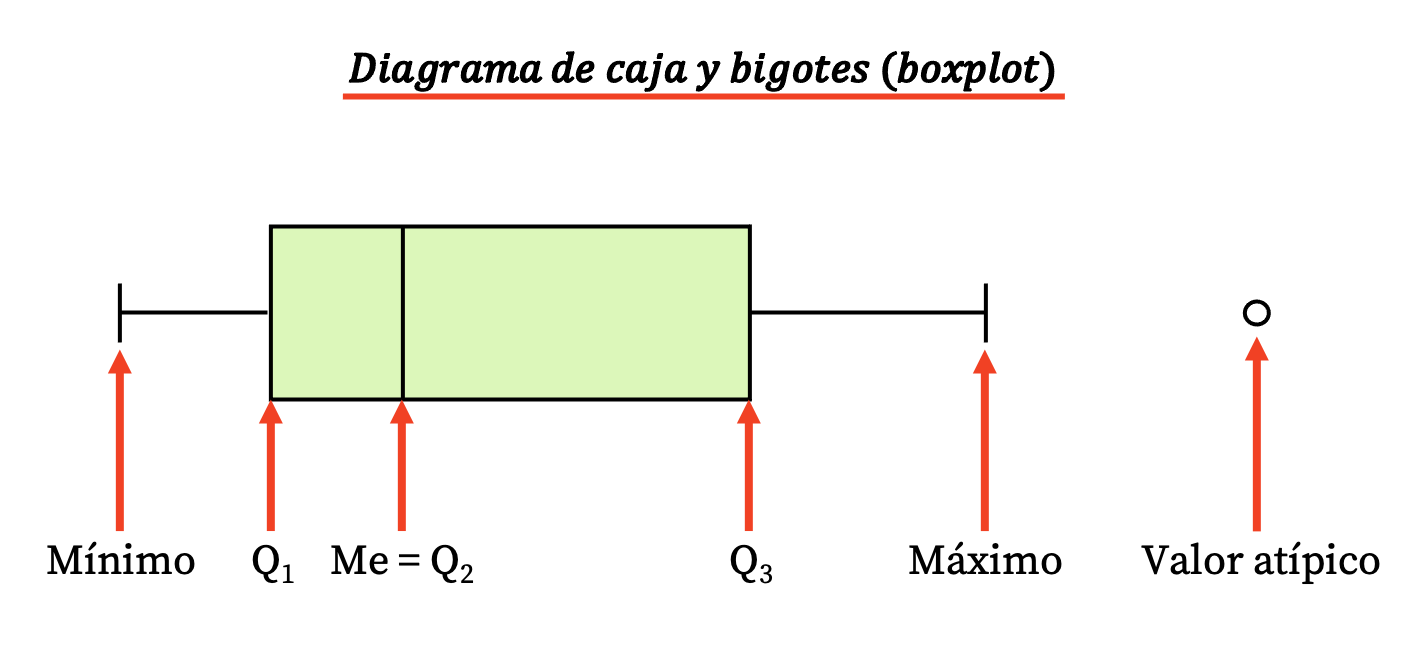
Perhatikan bahwa perbedaan antara kuartil ketiga dan pertama adalah rentang antarkuartil (atau rentang antarkuartil), yang merupakan ukuran lain dari penyebaran statistik.

Plot kotak dan kumis sangat berguna untuk membandingkan variabel numerik. Namun, ini tidak cocok untuk mewakili variabel kategori.

Cara Membuat Plot Kotak dan Kumis

Untuk membuat plot kotak dan kumis (atau plot kotak) dari serangkaian data, langkah-langkah berikut harus dilakukan:

Urutkan contoh data statistik.
Hitung kuartil (Q ₁ , Q ₂ dan Q ₃ ) dan nyatakan sebagai kotak pada diagram. Kuartil pertama dan ketiga sesuai dengan batas kotak, dan untuk mewakili median (kuartil kedua) Anda harus menggambar garis di dalam kotak tempat nilainya berada.
Hitung rentang antarkuartil, yang sama dengan kuartil ketiga dikurangi kuartil pertama.

$IQR=Q_3-Q_1$

Hitung nilai LI dan LS yang diperbolehkan, rumusnya adalah:

$LI=Q_1-1,5\cdot IQR$

$LS=Q_3+1,5\cdot IQR$

Identifikasi sampel outlier, yang nilainya lebih kecil dari LI atau lebih besar dari LS. Gambarkan nilai-nilai ini di luar rentang kumis dengan titik.
Identifikasi dan nyatakan nilai ekstrim, yaitu nilai terkecil dan nilai terbesar pada interval yang dibentuk oleh LI dan LS. Nilai-nilai ini mewakili akhir dari dua kumis pada diagram.

Contoh Plot Kotak dan Kumis

Mempertimbangkan definisi dan teori plot kotak dan kumis (atau plot kotak), di bawah ini Anda akan menemukan contoh konkret untuk lebih memahami konsep dan melihat bagaimana jenis plot statistik ini dilakukan.

Gambarlah diagram kotak dari kumpulan data statistik berikut.

Dalam hal ini data sudah diurutkan dari terkecil hingga terbesar, sehingga tidak perlu dilakukan perubahan. Jika tidak, kita harus mengurutkan data sampel terlebih dahulu.

Kedua, kami mengekstrak kuartil sampel:

$Q_1=4,06$

$Q_2=4,38$

$Q_3=4,66$

➤ Lihat: kalkulator kuartil

Setelah kita menghitung ketiga kuartil, kita mencari rentang antarkuartil dengan mengurangkan kuartil 3 dikurangi kuartil 1:

$IQR=Q_3-Q_1=4,66-4,06=0,6$

Kami sekarang menghitung batas LI dan LS, yang merupakan nilai yang datanya dianggap atipikal. Untuk melakukan ini, Anda harus menggunakan rumus berikut:

$LI=Q_1-1,5\cdot IQR=4,06-1,5\cdot 0,6=3,16$

$LS=Q_3+1,5\cdot IQR=4,66+1,5\cdot 0,6=5,56$

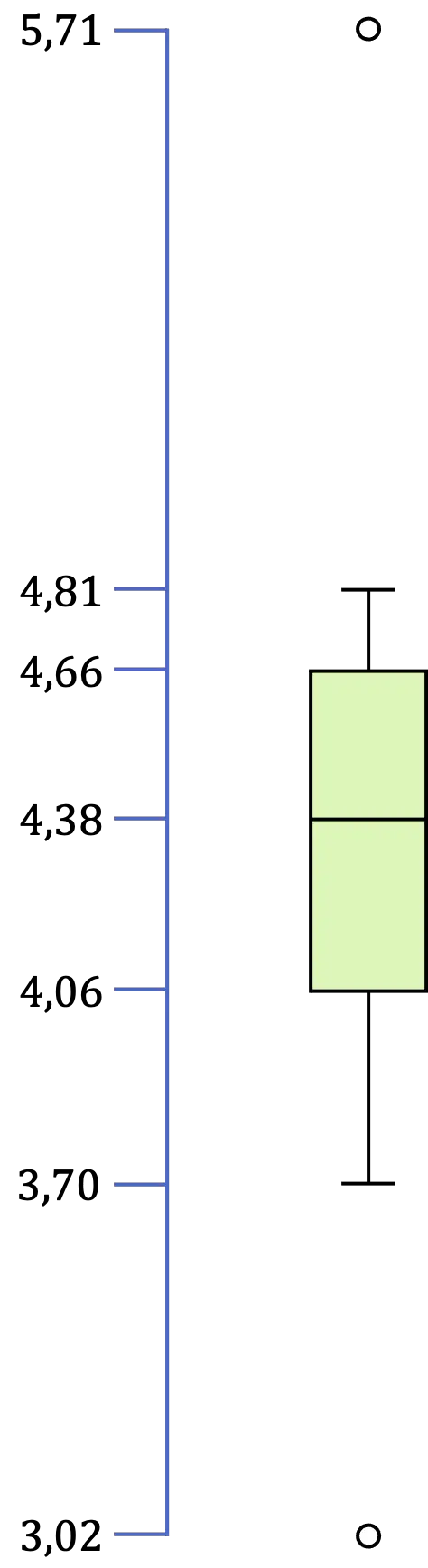
Jadi dalam kasus ini kita mempunyai dua outlier, karena 3,02 lebih kecil dari 3,16 dan 5,71 lebih besar dari 5,56.

$\text{Valores at\'ipicos} =\Bigl\{3,02 \ ; \ 5,71\Bigr\}$

Terakhir, tinggal mengidentifikasi nilai ekstrim yaitu nilai minimum dan maksimum dari seluruh data yang berada pada interval [LI,LS]. Oleh karena itu, dalam contoh kita, nilai minimumnya adalah 3,70 dan nilai maksimumnya adalah 4,81.

$\text{M\'inimo}=3,70$

$\text{M\'aximo}=4,81$

Jadi, setelah kita mengidentifikasi semua nilai plot kotak dan kumis, yang tersisa hanyalah membuat representasi grafis:

Plot kotak dan kumis digunakan untuk apa?

Terakhir, mari kita lihat untuk apa dan bagaimana menafsirkan plot kotak dan kumis (atau plot kotak).

Tentunya plot kotak dan garis sangat berguna untuk mengetahui dengan cepat kuartil, jangkauan antarkuartil, median, nilai ekstrim dan outlier dari suatu rangkaian data, karena semua ukuran statistik ini dapat diidentifikasi dengan pandangan sederhana.

Selain itu, plot kotak dan kumis digunakan untuk menganalisis simetri sampel statistik, karena secara visual mewakili seluruh kumpulan data. Jika mediannya tidak berada di tengah kotak berarti sampelnya tidak simetris.

Demikian pula, plot kotak banyak digunakan di pasar saham untuk mewakili variasi harga suatu saham selama periode waktu tertentu, karena memungkinkan seseorang untuk melihat nilai maksimum, nilai minimum, dan nilai antara dalam jangka waktu singkat. waktu dan dengan demikian membuat keputusan lebih cepat.

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya