Cara memplot hasil regresi linier berganda di r

Saat kita melakukan regresi linier sederhana di R, mudah untuk memvisualisasikan garis regresi yang dipasang karena kita hanya bekerja dengan satu variabel prediktor dan satu variabel respons .

Misalnya, kode berikut menunjukkan cara menyesuaikan model regresi linier sederhana ke kumpulan data dan memplot hasilnya:

 #create dataset
data <- data.frame(x = c(1, 1, 2, 4, 4, 5, 6, 7, 7, 8, 9, 10, 11, 11),
                   y = c(13, 14, 17, 23, 24, 25, 25, 24, 28, 32, 33, 35, 40, 41))

#fit simple linear regression model
model <- lm(y ~ x, data = data)

#create scatterplot of data
plot(data$x, data$y)

#add fitted regression line
abline(model)

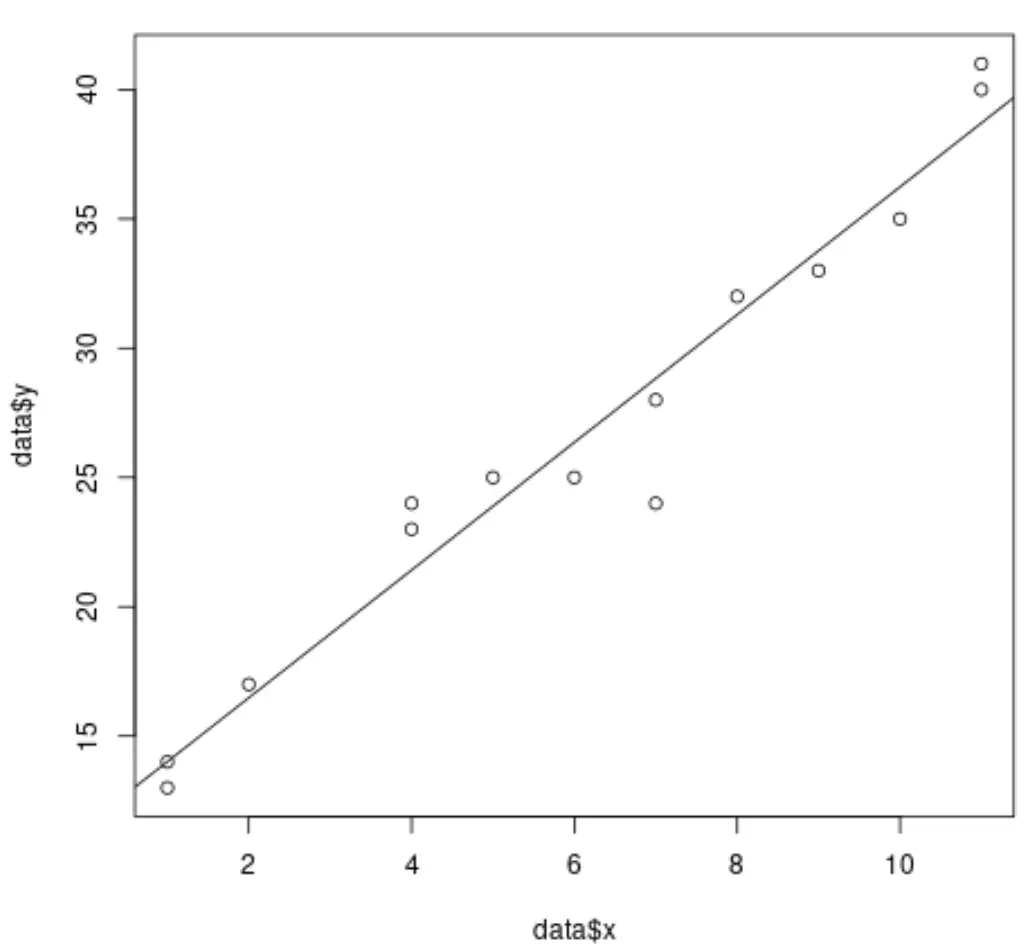
Namun, saat kita melakukan regresi linier berganda, memvisualisasikan hasilnya menjadi sulit karena terdapat beberapa variabel prediktor dan kita tidak bisa begitu saja memplot garis regresi pada grafik 2D.

Sebagai gantinya, kita dapat menggunakan plot variabel tambahan (terkadang disebut “plot regresi parsial”), yaitu plot individual yang menampilkan hubungan antara variabel respons dan variabel prediktor, sekaligus mengontrol keberadaan variabel prediktor lain dalam model .

Contoh berikut menunjukkan cara melakukan regresi linier berganda di R dan memvisualisasikan hasilnya menggunakan plot variabel yang ditambahkan.

Contoh: Merencanakan Hasil Regresi Linier Berganda di R

Misalkan kita menyesuaikan model regresi linier berganda berikut ke kumpulan data di R menggunakan kumpulan data mtcars bawaan:

 #fit multiple linear regression model
model <- lm(mpg ~ disp + hp + drat, data = mtcars)

#view results of model
summary(model)

Call:
lm(formula = mpg ~ disp + hp + drat, data = mtcars)

Residuals:
    Min 1Q Median 3Q Max 
-5.1225 -1.8454 -0.4456 1.1342 6.4958 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept) 19.344293 6.370882 3.036 0.00513 **
available -0.019232 0.009371 -2.052 0.04960 * 
hp -0.031229 0.013345 -2.340 0.02663 * 
drat 2.714975 1.487366 1.825 0.07863 . 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.008 on 28 degrees of freedom
Multiple R-squared: 0.775, Adjusted R-squared: 0.7509 
F-statistic: 32.15 on 3 and 28 DF, p-value: 3.28e-09

Dari hasil tersebut terlihat bahwa nilai p untuk masing-masing koefisien kurang dari 0,1. Untuk mempermudah, kita asumsikan bahwa masing-masing variabel prediktor adalah signifikan dan harus dimasukkan ke dalam model.

Untuk menghasilkan plot variabel yang ditambahkan, kita dapat menggunakan fungsi avPlots() dari paket car :

 #load car package
library(car)

#produce added variable plots
avPlots(model)

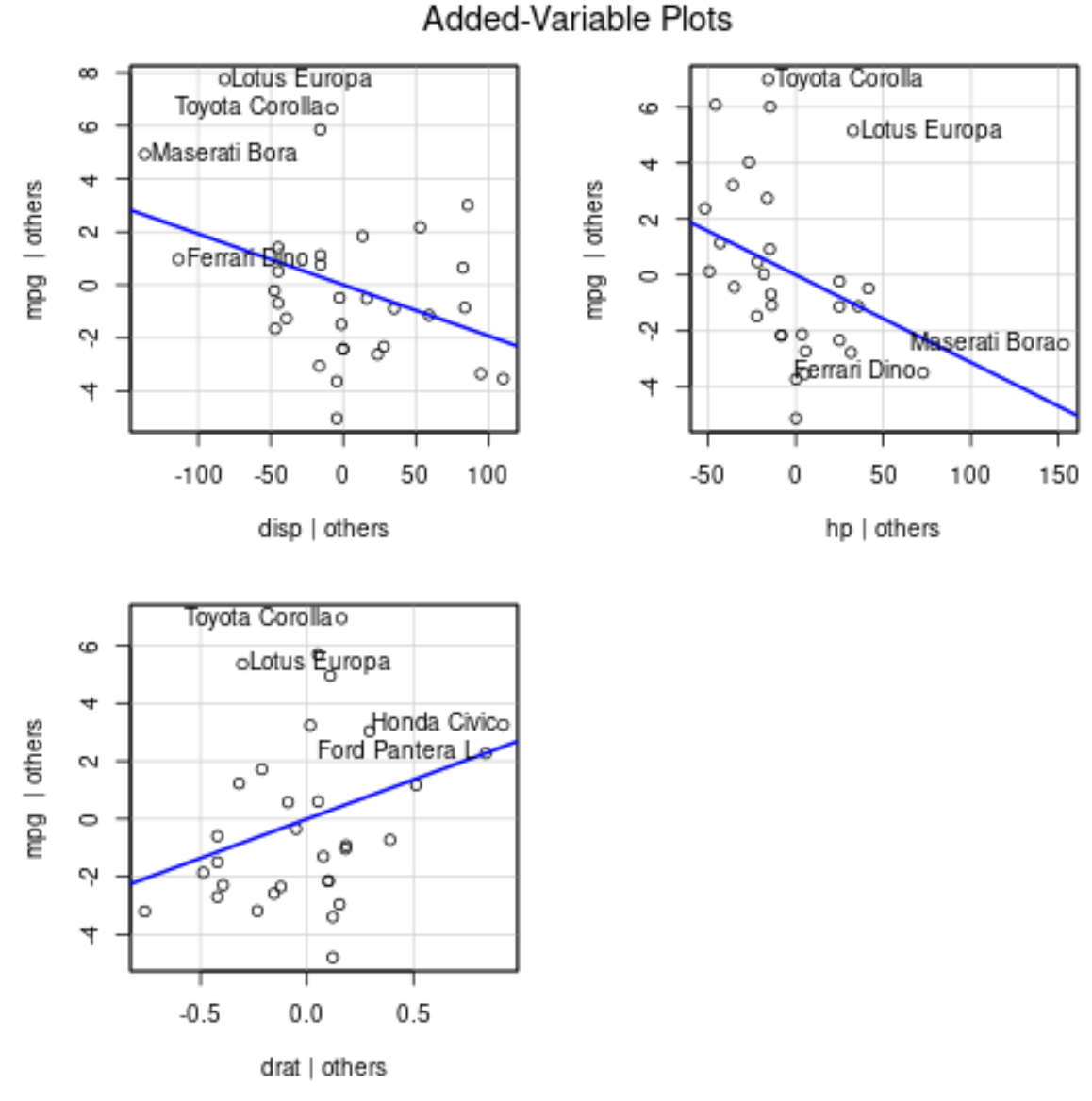
Berikut cara menafsirkan setiap plot:

• Sumbu x menampilkan satu variabel prediktor dan sumbu y menampilkan variabel respon.
• Garis biru menunjukkan hubungan antara variabel prediktor dan variabel respons, sementara nilai semua variabel prediktor lainnya tetap konstan .
• Titik-titik berlabel di setiap grafik mewakili 2 observasi dengan residu terbesar dan 2 observasi dengan leverage parsial terbesar.

Perhatikan bahwa sudut garis pada setiap plot sesuai dengan tanda koefisien persamaan regresi yang diestimasi.

Misalnya, berikut estimasi koefisien untuk setiap variabel prediktor dalam model:

• tampilan: -0,019232
• bab: -0,031229
• tanggal: 2.714975

Perhatikan bahwa sudut garis bernilai positif pada plot variabel yang ditambahkan untuk drat sedangkan sudut garis bernilai negatif untuk disp dan hp , yang sesuai dengan tanda estimasi koefisiennya:

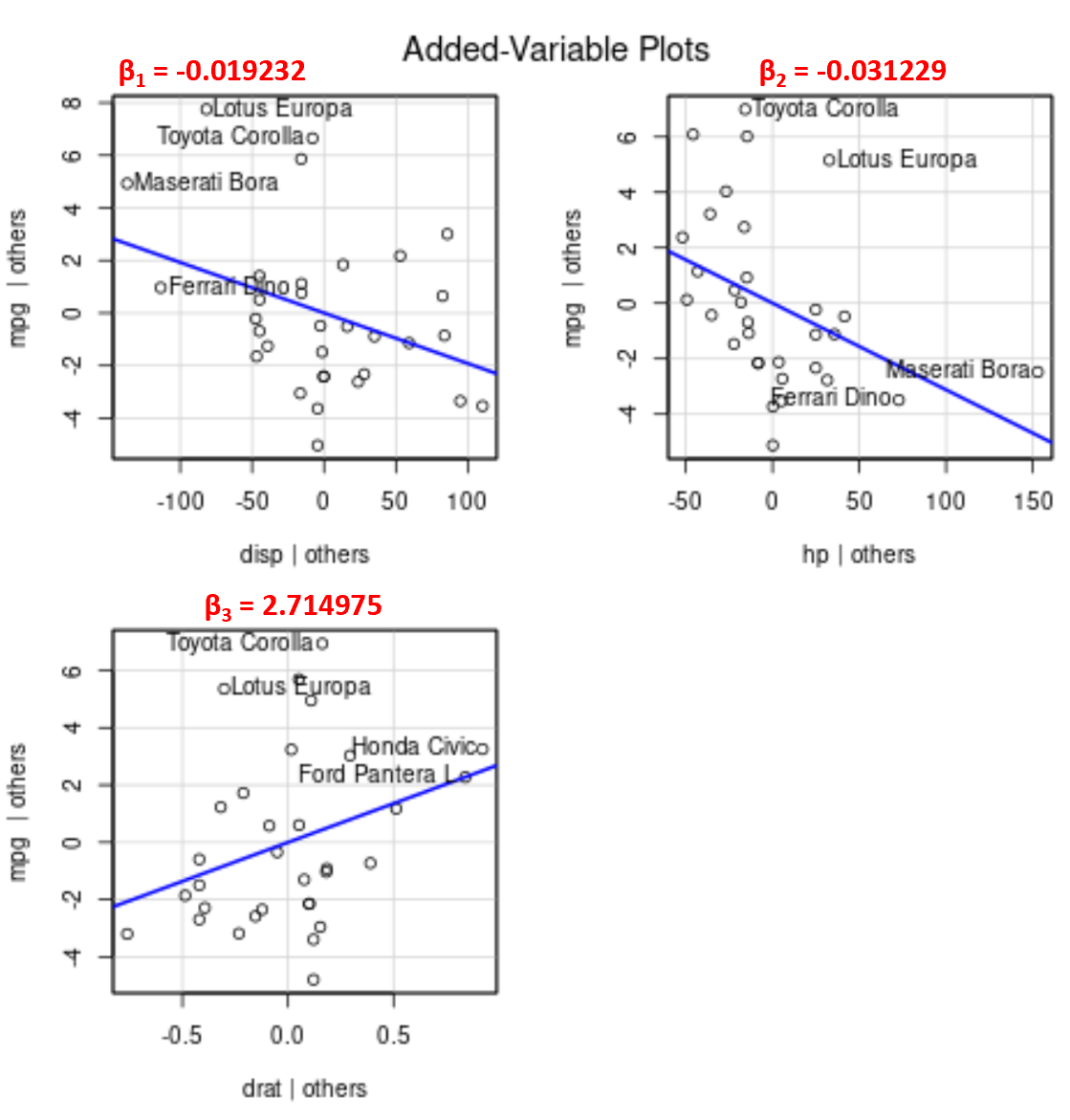
Meskipun kita tidak dapat memplot satu garis regresi yang terpasang pada grafik 2D karena kita memiliki beberapa variabel prediktor, grafik variabel tambahan ini memungkinkan kita untuk mengamati hubungan antara masing-masing variabel prediktor dan variabel respons sambil menjaga variabel prediktif lainnya tetap konstan.