Cara menghitung probabilitas binomial pada kalkulator ti-84

Distribusi binomial adalah salah satu distribusi yang paling umum digunakan dalam semua statistik. Tutorial ini menjelaskan cara menggunakan fungsi berikut pada kalkulator TI-84 untuk mencari probabilitas binomial:

binompdf(n, p, x) mengembalikan probabilitas yang terkait dengan binomial pdf.

binomcdf(n, p, x) mengembalikan probabilitas kumulatif yang terkait dengan binomial cdf.

Emas:

• n = jumlah percobaan
• p = probabilitas keberhasilan pada percobaan tertentu
• x = jumlah total keberhasilan

Kedua fungsi ini dapat diakses pada kalkulator TI-84 dengan menekan 2nd lalu menekan vars . Ini akan membawa Anda ke layar DISTR tempat Anda dapat menggunakan binompdf() dan binomcdf() :

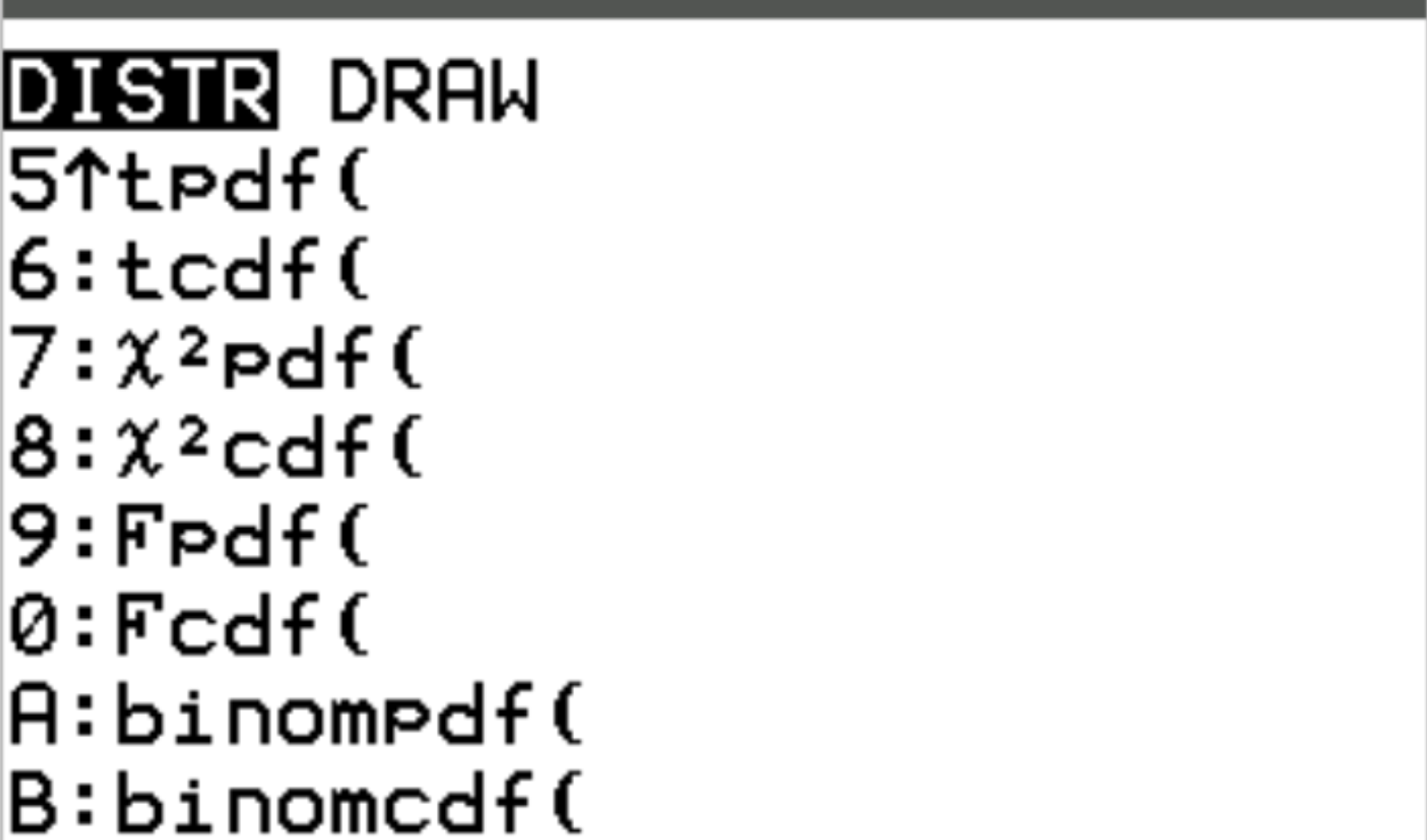
Contoh berikut mengilustrasikan cara menggunakan fungsi-fungsi ini untuk menjawab berbagai pertanyaan.

Contoh 1: Probabilitas binomial tepat x keberhasilan

Pertanyaan: Nathan melakukan 60% percobaan lemparan bebasnya. Jika dia melakukan 12 lemparan bebas, berapakah peluang dia berhasil tepat 10 lemparan bebas?

Jawaban: Gunakan fungsi binomialpdf(n, p, x):

binomialpdf(12, .60, 10) = 0,0639

Contoh 2: probabilitas binomial kurang dari x keberhasilan

Pertanyaan: Nathan melakukan 60% percobaan lemparan bebasnya. Jika dia melakukan 12 kali lemparan bebas, berapa peluang dia melakukan kurang dari 10 lemparan bebas?

Jawaban: Gunakan fungsi binomialcdf(n, p, x-1) :

binomialcdf(12, 0,60, 9) = 0,9166

Contoh 3: probabilitas binomial paling banyak x keberhasilan

Pertanyaan: Nathan melakukan 60% percobaan lemparan bebasnya. Jika dia melakukan 12 lemparan bebas, berapakah peluang dia melakukan lemparan bebas paling banyak 10?

Jawaban: Gunakan fungsi binomialcdf(n, p, x) :

binomialcdf(12, 0,60, 10) = 0,9804

Contoh 4: Probabilitas binomial lebih dari x keberhasilan

Pertanyaan: Nathan melakukan 60% percobaan lemparan bebasnya. Jika dia melakukan 12 kali lemparan bebas, berapa peluang dia melakukan lebih dari 10 lemparan bebas?

Jawaban: Gunakan fungsi 1 – binomialcdf(n, p, x) :

1 – binomialcdf(12, 0,60, 10) = 0,0196

Contoh 5: Probabilitas binomial minimal x keberhasilan

Pertanyaan: Nathan melakukan 60% percobaan lemparan bebasnya. Jika dia melakukan 12 kali lemparan bebas, berapa peluang dia melakukan lebih dari 10 lemparan bebas?

Jawaban: Gunakan fungsi 1 – binomialcdf(n, p, x-1) :

1 – binomialcdf(12, 0,60, 9) = 0,0834