Probabilitas empiris

Pada artikel ini kami menjelaskan cara menghitung probabilitas empiris. Anda akan mengetahui apa itu probabilitas empiris, apa rumusnya, contohnya dan apa perbedaan antara probabilitas empiris dan probabilitas teoritis.

Apa yang dimaksud dengan probabilitas empiris?

Probabilitas empiris adalah ukuran statistik yang didasarkan pada eksperimen atau fakta empiris yang menunjukkan kemungkinan terjadinya suatu peristiwa.

Dengan kata lain, probabilitas empiris dihitung dari hasil percobaan dan memberitahu kita seberapa besar kemungkinan suatu peristiwa akan terjadi.

Semakin sering percobaan diulang, maka probabilitas empiris yang diperoleh akan semakin tepat. Inilah sebabnya mengapa probabilitas jenis ini biasanya ditentukan menggunakan program komputer yang mensimulasikan ribuan iterasi dan mampu menganalisisnya dalam waktu yang sangat singkat.

Probabilitas empiris adalah bilangan antara 0 dan 1. Semakin besar kemungkinan terjadinya suatu peristiwa, maka semakin tinggi probabilitas empirisnya, dan sebaliknya, semakin kecil kemungkinan terjadinya suatu peristiwa, semakin rendah probabilitas empirisnya.

Rumus probabilitas empiris

Rumus probabilitas empiris adalah berapa kali suatu peristiwa terjadi selama suatu percobaan dibagi dengan berapa kali percobaan itu dilakukan.

Misalnya, jika kita melihat sebuah pohon sepuluh kali berbeda dan kita telah melihat seekor burung di pohon itu tujuh kali, probabilitas empiris kita melihat seekor burung sambil memandang pohon itu adalah:

Contoh Probabilitas Empiris

Dengan mempertimbangkan definisi probabilitas empiris, kita akan menyelesaikan latihan langkah demi langkah tentang jenis probabilitas ini. Dengan cara ini Anda dapat melihat bagaimana probabilitas empiris dihitung.

• Menghitung probabilitas empiris dari kejadian-kejadian dasar yang membentuk percobaan acak pelemparan sebuah dadu.

Pertama, kita akan menghitung probabilitas teoretis dengan membandingkan hasil eksperimen yang diperoleh dengan hasil teoretis. Ada enam kemungkinan hasil pelemparan sebuah dadu (1, 2, 3, 4, 5 dan 6), sehingga peluang teoritis setiap kejadian dasar adalah:

Untuk menyelesaikan latihan ini, kita harus melakukan simulasi pelemparan sebuah dadu beberapa kali dan mencatat hasilnya dalam tabel kontingensi. Untuk ini kita bisa menggunakan, misalnya program Excel.

Agar Anda dapat melihat pentingnya jumlah percobaan yang dilakukan, pertama-tama kami akan mensimulasikan sepuluh peluncuran, lalu seratus, dan terakhir seribu. Jadi, hasil yang diperoleh dari simulasi 10 kali pelemparan sebuah dadu secara acak adalah sebagai berikut:

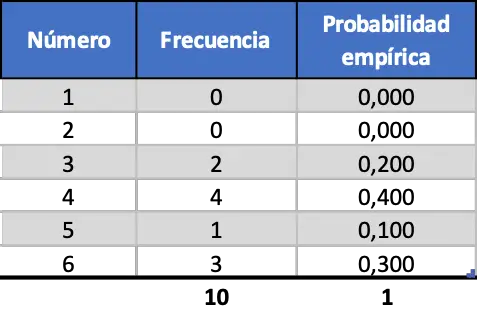
Seperti yang Anda lihat, probabilitas empiris yang diperoleh dengan mensimulasikan hanya sepuluh lemparan tidak mendekati probabilitas teoretis (0,167).

Namun seiring bertambahnya jumlah eksperimen, kedua metrik ini menjadi semakin mirip, lihat simulasi 100 peluncuran:

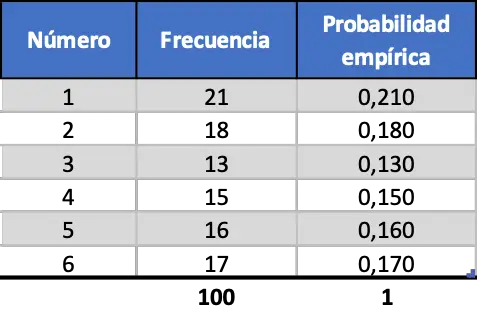
Sekarang probabilitas empiris yang dihitung untuk setiap angka pada dadu lebih mirip dengan probabilitas teoritis, namun kita masih mendapatkan nilai yang sangat berbeda.

Terakhir, kami melakukan prosedur yang sama tetapi mensimulasikan 1000 peluncuran:

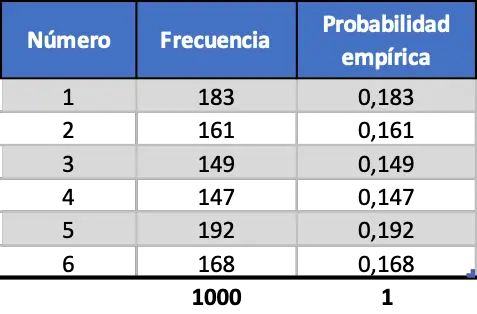
Seperti yang bisa kita lihat pada tabel kontingensi terakhir, kini nilai probabilitas empiris sangat dekat dengan probabilitas teoritis.

Singkatnya, semakin banyak kita menambah jumlah eksperimen yang dilakukan, semakin dekat nilai probabilitas empiris suatu peristiwa dengan probabilitas terjadinya teoritis . Aturan ini diartikan sebagai hukum bilangan besar , yang menyatakan bahwa semakin banyak data maka nilai eksperimen akan semakin mendekati nilai teoritis.

Lebih jauh lagi, jika kita membandingkan ketiga tabel frekuensi, kita melihat bahwa probabilitas empiris tidak pasti, tetapi berubah tergantung pada jumlah percobaan yang dilakukan. Artinya Anda harus mengetahui bagaimana cara mengartikan nilai-nilai yang diperoleh.

Probabilitas empiris dan probabilitas teoritis

Terakhir, kita akan menganalisis pengertian probabilitas empiris dan probabilitas teoretis, karena meskipun keduanya merupakan dua jenis probabilitas, keduanya memiliki arti yang sangat berbeda.

Perbedaan antara probabilitas empiris dan probabilitas teoretis (atau probabilitas klasik) adalah probabilitas empiris dihitung dari data yang dikumpulkan dari pengalaman nyata, sedangkan probabilitas teoretis dihitung dengan mempertimbangkan keadaan ideal tanpa melakukan eksperimen apa pun.

Artinya, untuk mencari probabilitas empiris, suatu eksperimen harus disimulasikan dan dilakukan perhitungan berdasarkan hasil yang diperoleh. Namun untuk mengetahui probabilitas teoritis, tidak perlu dilakukan eksperimen, melainkan perhitungan teoritis.

Selain itu, tingkat bias didefinisikan sebagai perbedaan antara probabilitas empiris dan probabilitas teoritis. Biasnya bisa positif atau negatif, tapi sangat sulit untuk mencapai nol, karena itu berarti eksperimen acak akan mencapai probabilitas teoretis, yang sangat kecil kemungkinannya.