Probabilitas posterior: definisi + contoh
Probabilitas posteriori adalah probabilitas terbaru bahwa suatu peristiwa akan terjadi setelah memperhitungkan informasi baru.
Misalnya, kita mungkin tertarik pada probabilitas terjadinya peristiwa “A” setelah memperhitungkan peristiwa “B” yang baru saja terjadi. Kita dapat menghitung probabilitas posterior ini menggunakan rumus berikut:
P(A|B) = P(A) * P(B|A) / P(B)
Emas:
P(A|B) = peluang terjadinya peristiwa A jika diketahui peristiwa B telah terjadi. Perhatikan bahwa “| » berarti “diberikan”.
P(A) = peluang terjadinya kejadian A.
P(B) = peluang terjadinya kejadian B.
P(B|A) = peluang terjadinya peristiwa B jika peristiwa A telah terjadi.
Contoh: Menghitung probabilitas posterior
Sebuah hutan terdiri dari 20% pohon ek dan 80% pohon maple. Misalkan kita mengetahui bahwa 90% pohon ek sehat sedangkan hanya 50% pohon maple yang sehat. Misalkan, dari kejauhan, Anda dapat mengetahui bahwa suatu pohon tertentu dalam keadaan sehat. Berapa peluang terambilnya pohon ek?
Ingatlah bahwa peluang terjadinya peristiwa A jika peristiwa B telah terjadi adalah:
P(A|B) = P(A) * P(B|A) / P(B)
Dalam contoh ini, peluang bahwa pohon tersebut adalah pohon oak jika pohon tersebut sehat adalah:
P(Oak|Sehat) = P(Oak) * P(Sehat|Oak) / P(Sehat)
P(Oak) = Peluang suatu pohon adalah pohon ek adalah 0,2 karena 20% dari seluruh pohon di hutan adalah pohon ek.
P(Sehat) = Peluang suatu pohon sehat dapat dihitung sebagai berikut: (0.20)*(0.9) + (0.8)*(0.5) = 0.58 .
P(Sehat|Oak) = Probabilitas suatu pohon sehat jika pohon tersebut merupakan pohon ek adalah 0,9 , karena kita telah diberitahu bahwa 90% pohon ek sehat.
Dengan menggunakan ketiga angka ini, kita dapat mencari probabilitas bahwa pohon tersebut adalah pohon ek jika pohon tersebut sehat:
P(Oak|Sehat) = P(Oak) * P(Sehat|Oak) / P(Sehat) = (0,2) * (0,9) / (0,58) = 0,3103 .
Untuk pemahaman intuitif tentang probabilitas ini, mari kita asumsikan bahwa grid berikut mewakili hutan yang terdiri dari 100 pohon. Tepatnya 20 pohon di antaranya adalah pohon ek dan 18 di antaranya sehat. 80 pohon lainnya adalah pohon maple dan 40 di antaranya sehat.
(O = Oak, M = Maple, Hijau = Sehat, Merah = Tidak Sehat)
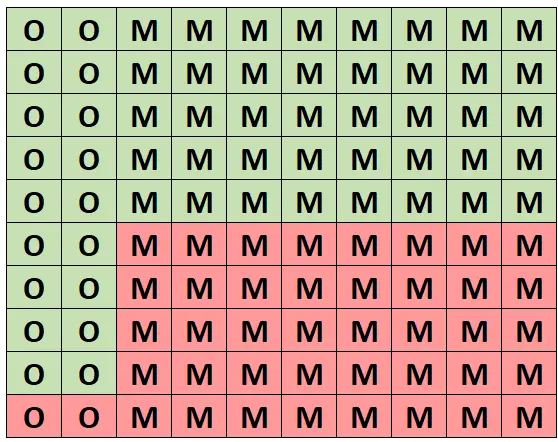
Dari seluruh pohon tersebut, tepatnya 58 pohon yang sehat dan 18 pohon yang sehat adalah pohon oak. Jadi, jika kita mengetahui bahwa kita telah memilih pohon yang sehat, maka peluang terambilnya pohon ek adalah 18/58 = 0,3103 .
Kapan sebaiknya Anda menggunakan probabilitas posterior?
Probabilitas posterior digunakan dalam berbagai bidang, termasuk keuangan, kedokteran, ekonomi, dan prakiraan cuaca.
Tujuan penggunaan probabilitas posterior adalah untuk memperbarui keyakinan kita sebelumnya tentang sesuatu setelah kita memperoleh informasi baru.
Ingat contoh sebelumnya bahwa kita mengetahui bahwa probabilitas bahwa suatu pohon di hutan adalah pohon ek adalah 20%. Ini disebut probabilitas sebelumnya . Jika kita memilih sebuah pohon secara acak, kita mengetahui bahwa probabilitas pohon tersebut adalah pohon ek adalah 0,20.
Namun, setelah kami mendapatkan informasi baru bahwa pohon yang kami pilih adalah pohon yang sehat, kami dapat menggunakan informasi baru ini untuk menentukan bahwa probabilitas posterior pohon tersebut adalah pohon ek adalah 0,3103.
Di dunia nyata, orang terus-menerus menemukan informasi baru. Informasi baru ini membantu kita memperbarui keyakinan kita sebelumnya. Dalam istilah statistik, ini berarti kita dapat menghasilkan probabilitas posterior dari peristiwa yang terjadi, yang membantu kita memperoleh pemahaman dunia yang lebih akurat dan memungkinkan kita membuat prediksi yang lebih akurat tentang peristiwa di masa depan.