Cara melakukan regresi kubik dengan python

Regresi kubik merupakan salah satu jenis regresi yang dapat kita gunakan untuk mengukur hubungan antara variabel prediktor dan variabel respon jika hubungan antar variabel bersifat nonlinier.

Tutorial ini menjelaskan cara melakukan regresi kubik dengan Python.

Contoh: regresi kubik dengan Python

Misalkan kita memiliki panda DataFrame berikut yang berisi dua variabel (x dan y):

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' x ': [6, 9, 12, 16, 22, 28, 33, 40, 47, 51, 55, 60],
                   ' y ': [14, 28, 50, 64, 67, 57, 55, 57, 68, 74, 88, 110]})

#view DataFrame
print (df)

     xy
0 6 14
1 9 28
2 12 50
3 16 64
4 22 67
5 28 57
6 33 55
7 40 57
8 47 68
9 51 74
10 55 88
11 60 110

Jika kita membuat diagram sebar sederhana dari data ini, kita dapat melihat bahwa hubungan antara kedua variabel adalah non-linier:

 import matplotlib. pyplot as plt

#create scatterplot
plt. scatter (df. x , df. y ) 

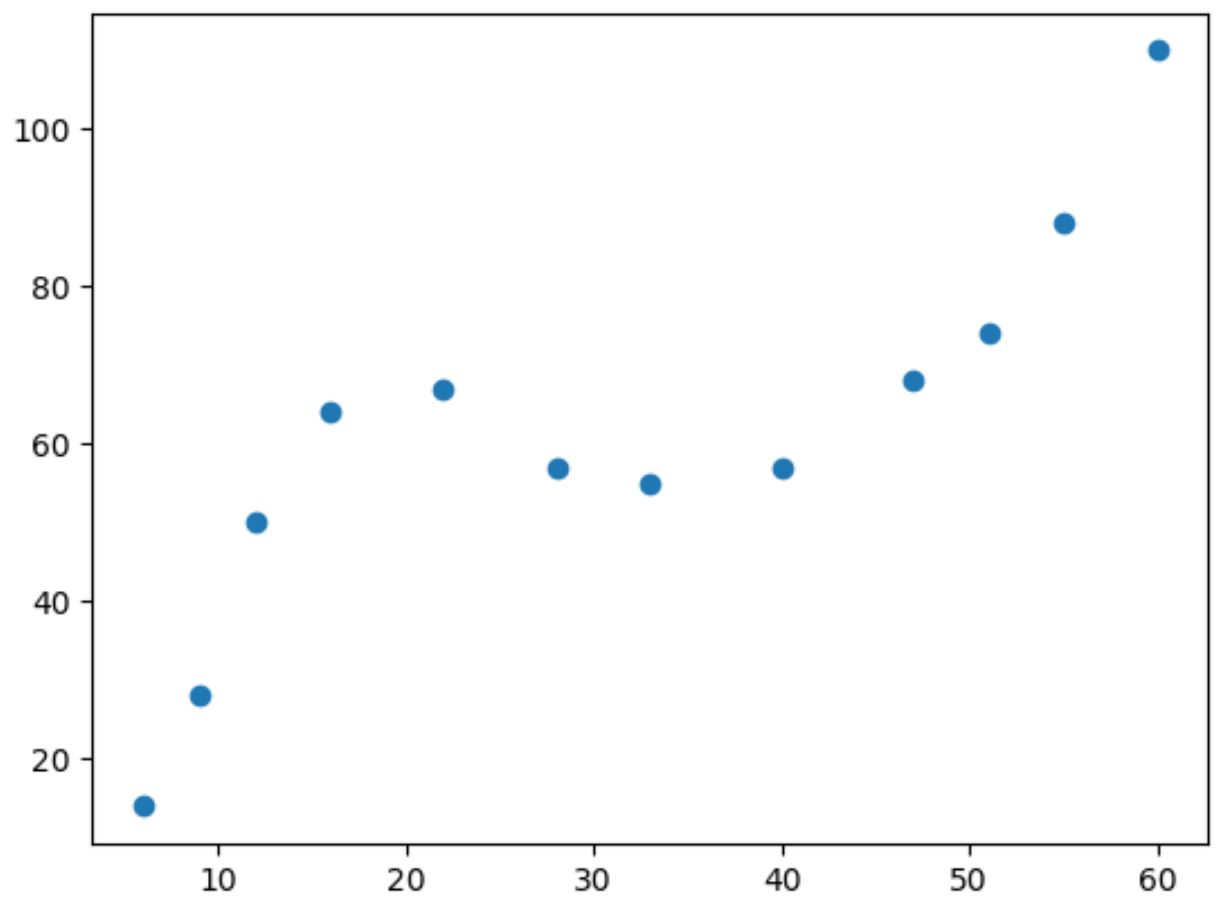
Ketika nilai x meningkat, y meningkat hingga titik tertentu, lalu menurun, lalu meningkat lagi.

Pola dengan dua “kurva” pada plot ini merupakan indikasi hubungan kubik antara kedua variabel.

Artinya model regresi kubik merupakan kandidat yang baik untuk mengukur hubungan antara kedua variabel.

Untuk melakukan regresi kubik, kita dapat menyesuaikan model regresi polinomial dengan derajat 3 menggunakan fungsi numpy.polyfit() :

 import numpy as np

#fit cubic regression model
model = np. poly1d (np. polyfit (df. x , df. y , 3))

#add fitted cubic regression line to scatterplot
polyline = np. linspace (1, 60, 50)
plt. scatter (df. x , df. y )
plt. plot (polyline, model(polyline))

#add axis labels
plt. xlabel (' x ')
plt. ylabel (' y ')

#displayplot
plt. show () 

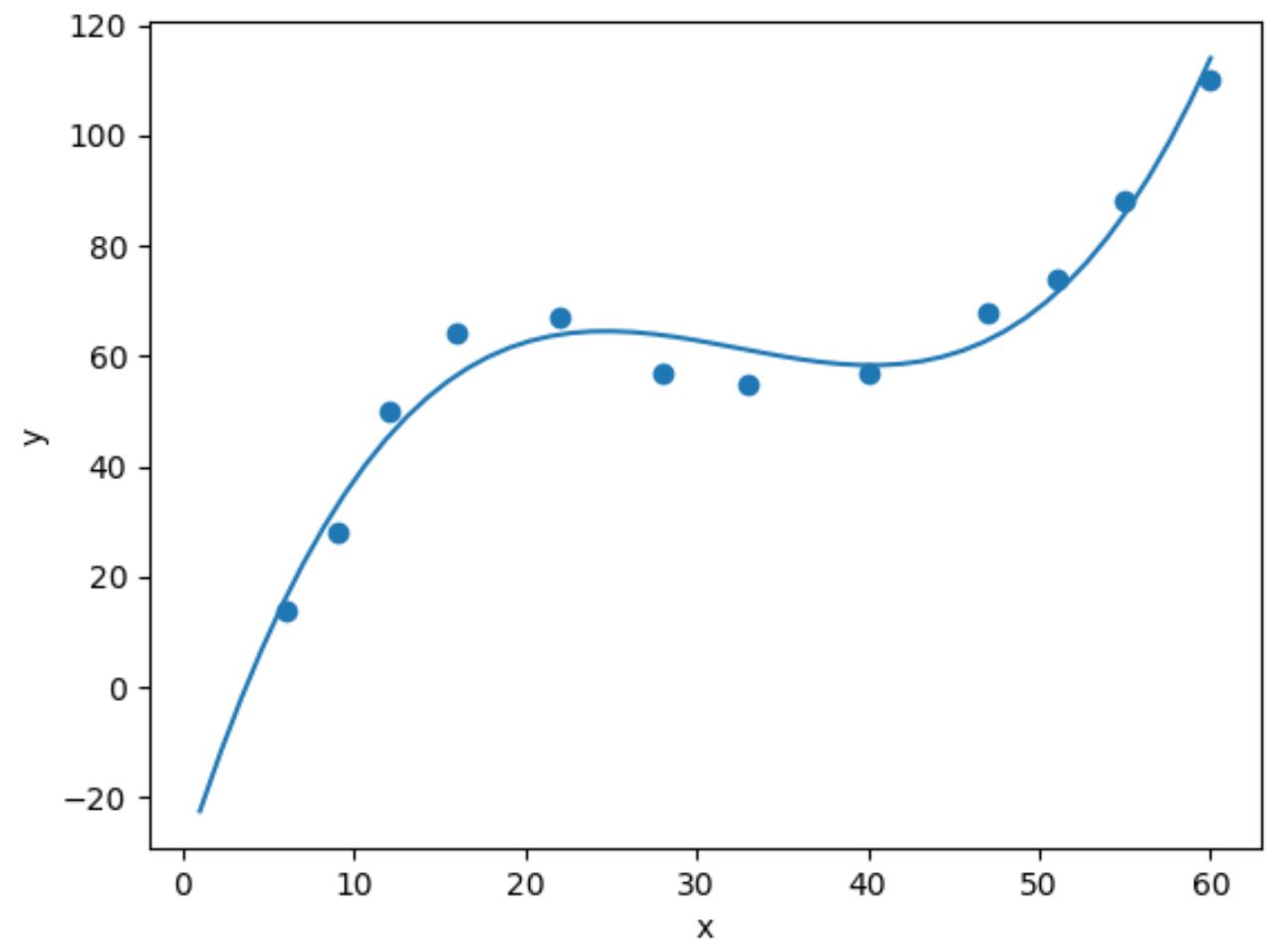
Kita dapat memperoleh persamaan regresi kubik dengan mencetak koefisien model:

 print (model)

          3 2
0.003302x - 0.3214x + 9.832x - 32.01

Persamaan regresi kubik yang pas adalah:

kamu = 0,003302(x) ³ – 0,3214(x) ² + 9,832x – 30,01

Kita dapat menggunakan persamaan ini untuk menghitung nilai ekspektasi y berdasarkan nilai x.

Misalnya, jika x adalah 30, maka nilai yang diharapkan untuk y adalah 64,844:

kamu = 0,003302(30) ³ – 0,3214(30) ² + 9,832(30) – 30,01 = 64,844

Kita juga dapat menuliskan fungsi singkat untuk mendapatkan R-squared model, yaitu proporsi varians variabel respon yang dapat dijelaskan oleh variabel prediktor.

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = np. polyfit (x, y, degree)
    p = np. poly1d (coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = np. sum (y)/len(y)
    ssreg = np. sum ((yhat-ybar) ** 2)
    sstot = np. sum ((y - ybar) ** 2)
    results[' r_squared '] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(df. x , df. y , 3)

{'r_squared': 0.9632469890057967}

Dalam contoh ini, R kuadrat model adalah 0,9632 .

Artinya 96,32% variasi variabel respon dapat dijelaskan oleh variabel prediktor.

Karena nilai ini sangat tinggi, hal ini menunjukkan bahwa model regresi kubik dapat mengkuantifikasi hubungan antara kedua variabel dengan baik.

Terkait: Berapa nilai R-kuadrat yang bagus?

Sumber daya tambahan

Tutorial berikut menjelaskan cara melakukan tugas umum lainnya dengan Python:

Cara melakukan regresi linier sederhana dengan Python
Cara melakukan regresi kuadrat dengan Python
Cara melakukan regresi polinomial dengan Python