Cara melakukan regresi polinomial dengan python

Analisis regresi digunakan untuk mengukur hubungan antara satu atau lebih variabel penjelas dan variabel respon.

Jenis analisis regresi yang paling umum adalah regresi linier sederhana , digunakan ketika variabel prediktor dan variabel respons mempunyai hubungan linier.

Namun terkadang hubungan antara variabel prediktor dan variabel respon bersifat nonlinier.

Misalnya, hubungan sebenarnya mungkin berbentuk kuadrat:

Atau bisa juga kubik:

Dalam kasus ini, masuk akal untuk menggunakan regresi polinomial , yang dapat menjelaskan hubungan nonlinier antar variabel.

Tutorial ini menjelaskan cara melakukan regresi polinomial dengan Python.

Contoh: Regresi Polinomial dengan Python

Misalkan kita memiliki variabel prediktor (x) dan variabel respon (y) berikut dengan Python:

 x = [2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12]
y = [18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29]

Jika kita membuat diagram sebar sederhana dari data ini, kita dapat melihat bahwa hubungan antara x dan y jelas tidak linier:

 import matplotlib.pyplot as plt

#create scatterplot 
plt.scatter(x, y)

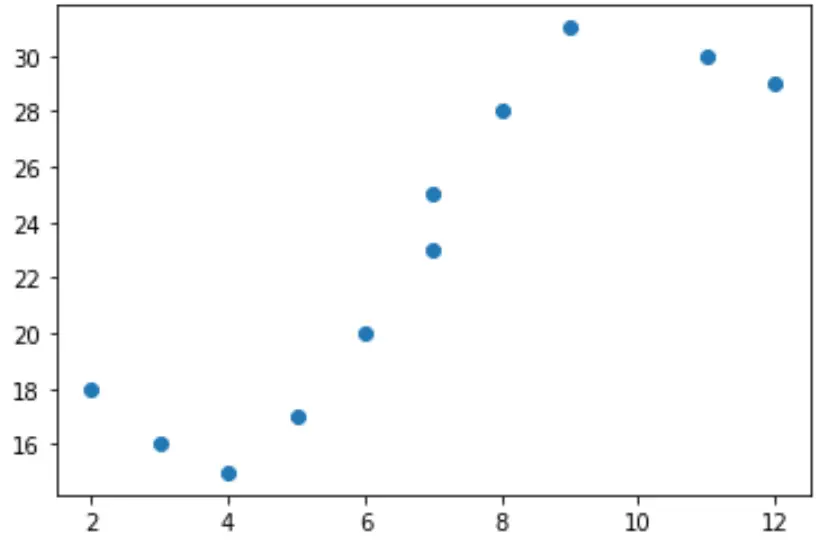
Oleh karena itu, tidak masuk akal untuk menyesuaikan model regresi linier dengan data ini. Sebagai gantinya, kita dapat mencoba menyesuaikan model regresi polinomial dengan derajat 3 menggunakan fungsi numpy.polyfit() :

 import numpy as np

#polynomial fit with degree = 3
model = np.poly1d(np.polyfit(x, y, 3))

#add fitted polynomial line to scatterplot
polyline = np.linspace(1, 12, 50)
plt.scatter(x, y)
plt.plot(polyline, model(polyline))
plt.show() 

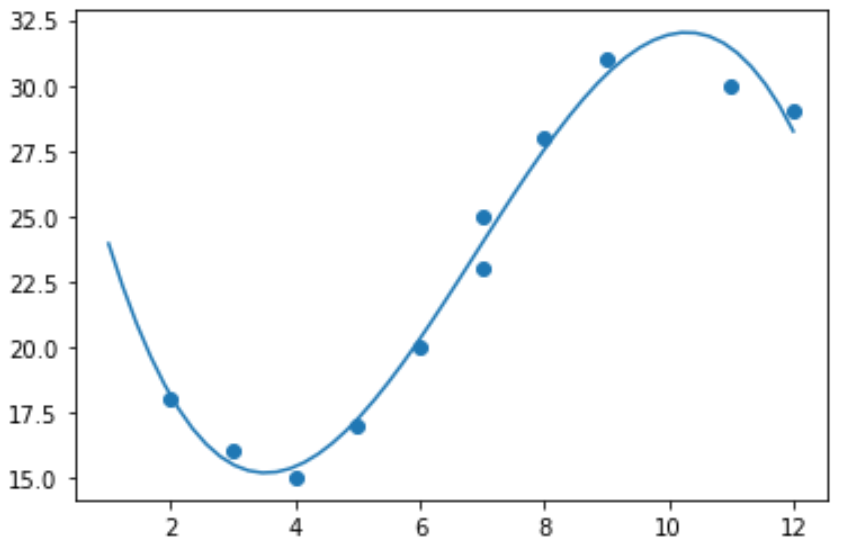
Kita dapat memperoleh persamaan regresi polinomial yang sesuai dengan mencetak koefisien model:

 print(model)

poly1d([ -0.10889554, 2.25592957, -11.83877127, 33.62640038])

Persamaan regresi polinomial yang dipasang adalah:

kamu = -0,109x ³ + 2,256x ² – 11,839x + 33,626

Persamaan ini dapat digunakan untuk mencari nilai yang diharapkan dari variabel respon jika diberi nilai variabel penjelas tertentu.

Misalnya, asumsikan x = 4. Nilai yang diharapkan untuk variabel respon, y, adalah:

kamu = -0,109(4) ³ + 2,256(4) ² – 11,839(4) + 33,626= 15,39 .

Kita juga dapat menuliskan fungsi singkat untuk mendapatkan R-squared model, yaitu proporsi varians variabel respon yang dapat dijelaskan oleh variabel prediktor.

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = numpy.polyfit(x, y, degree)
    p = numpy.poly1d(coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = numpy.sum(y)/len(y)
    ssreg = numpy.sum((yhat-ybar)**2)
    sstot = numpy.sum((y - ybar)**2)
    results['r_squared'] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(x, y, 3)

{'r_squared': 0.9841113454245183}

Dalam contoh ini, R kuadrat model adalah 0,9841 .

Artinya 98,41% variasi variabel respon dapat dijelaskan oleh variabel prediktor.