Rasio odds yang disesuaikan: definisi + contoh

Dalam statistik, rasio odds menunjukkan kepada kita rasio antara probabilitas suatu peristiwa terjadi pada kelompok perlakuan dan probabilitas suatu peristiwa terjadi pada kelompok kontrol.

Rasio peluang paling sering muncul dalam regresi logistik , yaitu metode yang kami gunakan untuk menyesuaikan model regresi yang memiliki satu atau lebih variabel prediktor dan variabel respons biner.

Rasio odds yang disesuaikan adalah rasio odds yang telah disesuaikan dengan variabel prediktor lain dalam suatu model.

Hal ini sangat berguna dalam membantu kita memahami bagaimana variabel prediktor mempengaruhi peluang terjadinya suatu peristiwa, setelah disesuaikan dengan pengaruh variabel prediktor lainnya.

Contoh berikut mengilustrasikan perbedaan antara rasio odds dan rasio odds yang disesuaikan.

Contoh: Perhitungan rasio odds yang disesuaikan

Misalkan kita ingin memahami apakah usia seorang ibu mempengaruhi kemungkinan memiliki bayi dengan berat badan lahir rendah.

Untuk mengetahui hal tersebut, kita dapat melakukan regresi logistik dengan menggunakan usia sebagai variabel prediktor dan berat badan lahir rendah (ya atau tidak) sebagai variabel respon .

Misalkan kita mengumpulkan data dari 300 ibu dan menyesuaikan model regresi logistik. Berikut hasilnya:

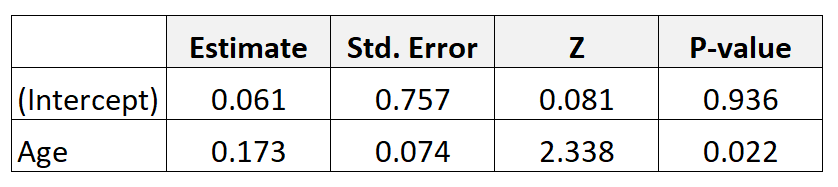
Untuk memperoleh rasio odds usia, cukup eksponensial estimasi koefisien dari tabel: e ^0,173 = 1,189 .

Hal ini menunjukkan bahwa peningkatan usia satu tahun dikaitkan dengan peningkatan 1.189 kemungkinan bayi memiliki berat badan lahir rendah. Dengan kata lain, peluang melahirkan bayi dengan berat badan lahir rendah meningkat sebesar 18,9% untuk setiap penambahan usia tahunan.

Rasio odds ini disebut rasio odds “kasar” atau rasio odds “tidak disesuaikan” karena belum disesuaikan dengan variabel prediktor lain dalam model karena merupakan satu-satunya variabel prediktor dalam model.

Namun misalkan kita ingin memahami apakah usia ibu dan kebiasaan merokok mempengaruhi kemungkinan memiliki bayi dengan berat badan lahir rendah.

Untuk mengeksplorasi hal ini, kita dapat melakukan regresi logistik dengan menggunakan usia dan merokok (ya atau tidak) sebagai variabel prediktor dan berat badan lahir rendah sebagai variabel respon .

Misalkan kita mengumpulkan data dari 300 ibu dan menyesuaikan model regresi logistik. Berikut hasilnya:

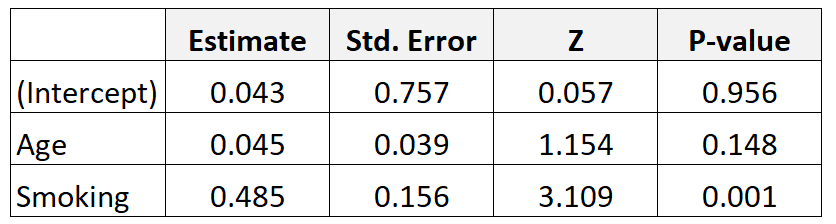
Berikut cara menafsirkan hasilnya:

Usia: Rasio odds yang disesuaikan usia dihitung sebagai berikut: e ^0,045 = 1,046 . Artinya peluang melahirkan bayi dengan berat badan lahir rendah meningkat sebesar 4,6% untuk setiap penambahan usia tahunan, dengan asumsi variabel merokok tetap.

Misalnya Ibu A dan Ibu B sama-sama merokok. Apabila ibu A berumur satu tahun lebih tua dari ibu B, maka peluang ibu A mempunyai bayi berat lahir rendah adalah 1,046 kali peluang ibu B mempunyai bayi berat lahir rendah.

Merokok : Rasio odds yang disesuaikan untuk merokok dihitung sebagai berikut: ^e.485 = 1.624 . Artinya peluang mempunyai bayi dengan berat badan lahir rendah meningkat sebesar 62,4% jika ibu merokok (dibandingkan tidak merokok), dengan asumsi variabel umur tetap.

Misalnya Ibu A dan Ibu B sama-sama berumur 30 tahun. Jika ibu A merokok saat hamil dan ibu B tidak merokok, maka peluang ibu A melahirkan bayi berat lahir rendah 62,4% lebih tinggi dibandingkan peluang ibu B melahirkan bayi berat lahir rendah.

Perhatikan bahwa rasio odds yang disesuaikan dengan usia lebih rendah daripada rasio odds yang tidak disesuaikan dari contoh sebelumnya. Hal ini karena ketika variabel prediktor lain meningkatkan kemungkinan terjadinya variabel respon, maka rasio odds yang disesuaikan untuk variabel prediktor yang sudah ada dalam model akan selalu menurun.

Ringkasan: rasio odds versus rasio odds yang disesuaikan

Rasio odds (terkadang disebut rasio odds “kasar”) berguna untuk memberi tahu kita bagaimana perubahan dalam variabel prediktor mempengaruhi peluang terjadinya variabel respons.

Rasio odds yang disesuaikan berguna untuk memberi tahu kita bagaimana perubahan dalam variabel prediktor memengaruhi peluang terjadinya variabel respons, setelah mengontrol variabel prediktor lain dalam suatu model.

Sumber daya tambahan

Pengantar Regresi Logistik
Bagaimana melakukan regresi logistik di R
Cara Melakukan Regresi Logistik dengan Python