Rata-rata aritmatika

Oleh Benjamin anderson Agustus 6, 2023 Statistik 0 Komentar

Di sini kami menjelaskan apa itu mean aritmatika dan cara menghitungnya. Anda akan menemukan contoh rata-rata aritmatika dan bahkan kalkulator untuk mencari rata-rata aritmatika dari sampel statistik apa pun. Terakhir, Anda akan dapat melihat apa saja sifat-sifat rata-rata jenis ini dan bagaimana rata-rata aritmatika diperoleh dengan data yang dikelompokkan ke dalam interval.

Apa yang dimaksud dengan aritmatika?

Rata-rata aritmatika adalah karakteristik nilai sentral dari sekumpulan data statistik. Untuk menghitung mean aritmatika, semua nilai dijumlahkan dan dibagi dengan jumlah total data.

Selain itu, mean aritmatika adalah salah satu indikator utama yang digunakan untuk melakukan studi statistik terhadap suatu sampel.

Oleh karena itu, rumus rata-rata aritmatika adalah sebagai berikut:

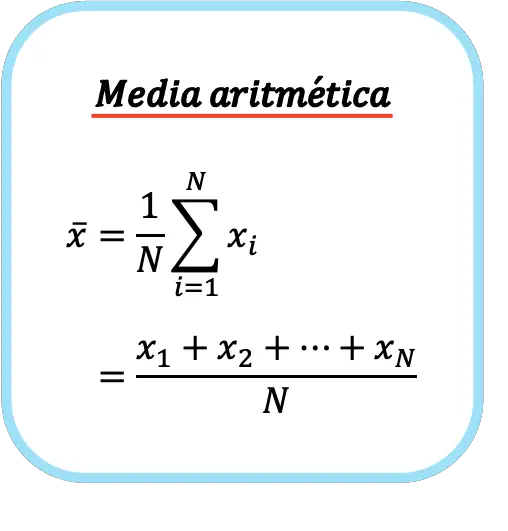
Simbol mean aritmatika adalah garis horizontal di atas huruf x.

$(\overline{x}).$

Anda juga dapat membedakan mean sampel dari mean populasi dengan simbol mean: mean sampel dinyatakan dengan simbol

$\overline{x}$

, sebaliknya, untuk rata-rata suatu populasi, kami menggunakan huruf Yunani

$\mu.$

Perlu dicatat bahwa rata-rata aritmatika suatu populasi setara dengan nilai yang diharapkan dari variabel statistik.

Rata-rata aritmatika, disebut juga mean aritmatika, bukan satu-satunya jenis mean yang ada, ada juga mean tertimbang, mean kuadrat, mean geometrik, dan mean harmonik, antara lain. Anda dapat melihat bagaimana masing-masing dihitung di mesin pencari situs web kami.

Cara menghitung mean aritmatika

Untuk menghitung mean aritmatika, langkah-langkah berikut harus dilakukan:

Tambahkan semua data statistik dari sampel.
Bagilah jumlah sebelumnya dengan jumlah total data.
Hasil yang diperoleh adalah mean aritmatika dari sampel statistik.

👉 Anda dapat menggunakan kalkulator di bawah ini untuk menghitung rata-rata aritmatika dari kumpulan data apa pun.

Contoh penghitungan mean aritmatika

Mengingat definisi mean aritmatika, kita akan melihat cara mendapatkan mean aritmatika dari sekumpulan data dengan menyelesaikan contoh langkah demi langkah.

Seorang siswa mencapai nilai berikut selama satu tahun ajaran: dalam matematika a 9, dalam bahasa a 7, dalam sejarah a 6, dalam ekonomi a 8 dan dalam sains a 7.5. Berapa rata-rata aritmatika dari semua nilai Anda?

Untuk mencari rata-rata aritmatika, kita perlu menjumlahkan semua nilai lalu membaginya dengan jumlah seluruh mata pelajaran pada mata kuliah tersebut, yaitu 5. Oleh karena itu, kita menerapkan rumus rata-rata aritmatika:

$\displaystyle\overline{x}=\frac{1}{N}\sum_{i=1}^N x_i=\frac{x_1+x_2+x_3+x_4+x_5}{N}$

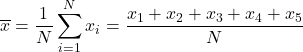
Kami mengganti data ke dalam rumus dan menghitung rata-rata aritmatika:

$\overline{x}=\cfrac{9+7+5+8+7,5}{5}=7,3$

Seperti yang Anda lihat, dalam rata-rata aritmatika, bobot yang sama diberikan untuk setiap nilai, yaitu setiap bagian data memiliki bobot yang sama secara keseluruhan.

Kalkulator Rata-Rata Aritmatika

Masukkan data dari sampel statistik apa pun ke dalam kalkulator berikut untuk menghitung rata-rata aritmatikanya. Data harus dipisahkan dengan spasi dan dimasukkan menggunakan titik sebagai pemisah desimal.

Rata-rata aritmatika untuk data yang dikelompokkan

Yang kami maksud dengan data berkelompok adalah data disusun dalam kelompok atau interval. Hal ini biasanya terjadi bila ukuran sampel statistik sangat besar.

Jadi perhitungan mean aritmatikanya sedikit berbeda ketika datanya dikelompokkan, padahal konsepnya sama.

Untuk menghitung rata-rata aritmatika data yang dikelompokkan ke dalam interval, skor kelas masing-masing kelompok harus dikalikan dengan frekuensi absolutnya lalu dibagi dengan jumlah seluruh frekuensi absolut.

$\displaystyle\overline{x}=\frac{\sum_{i=1}^N x_i\cdot f_i}{\sum_{i=1}^N f_i} =\frac{x_1\cdot f_1+ x_2\cdot f_2+\dots +x_N\cdot f_N}{N}$

Catatan: Skor kelas suatu interval dihitung dengan membagi jumlah titik akhir interval dengan dua. Misalnya, catatan kelas pada interval [3,7) adalah:

$\cfrac{3+7}{2}=5$

Agar Anda dapat melihat bagaimana hal ini dilakukan, di bawah ini adalah latihan penyelesaian rata-rata aritmatika dari data yang dikelompokkan ke dalam interval:

Kami ingin mempelajari bobot suatu kelompok secara statistik, untuk ini kami mewawancarai perwakilan kelompok yang terdiri dari 81 orang dan kami memperoleh data berikut:

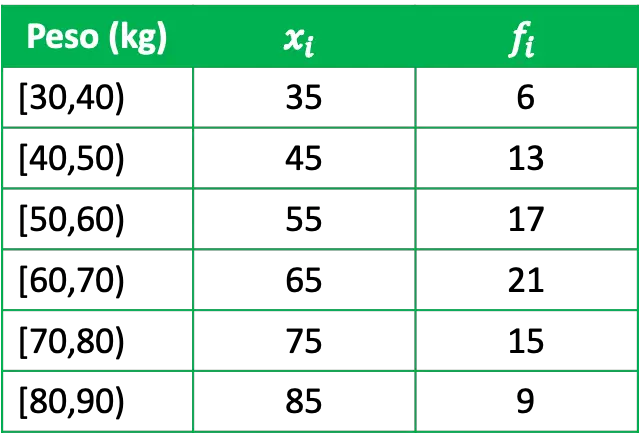
Dimana x _i adalah skor kelas masing-masing kelompok dan f _{i adalah} frekuensi absolutnya, yaitu jumlah orang yang mempunyai bobot dalam interval tersebut.

Untuk menentukan mean aritmatika, perlu ditambahkan kolom pada tabel frekuensi yang merupakan hasil kali catatan kelas dengan frekuensi absolutnya masing-masing:

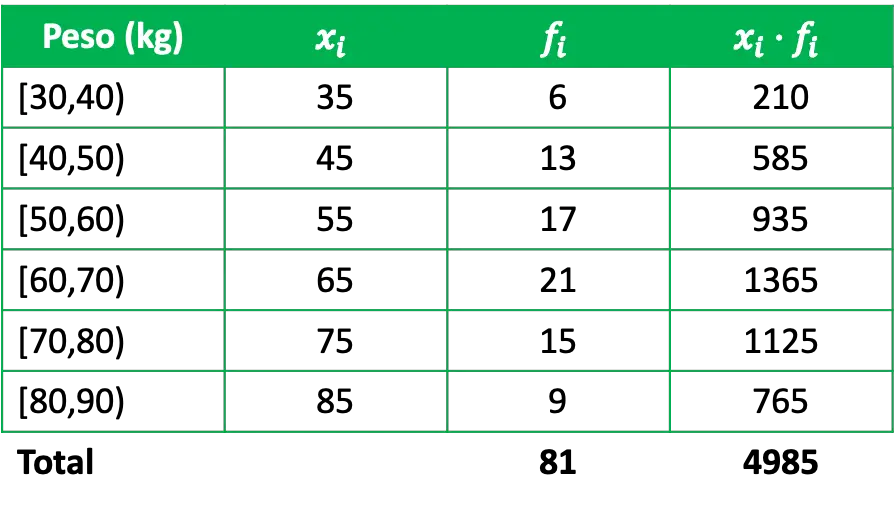
latihan rata-rata aritmatika diselesaikan untuk data yang dikelompokkan

Jadi, untuk menghitung rata-rata aritmatika dari data yang dikelompokkan, cukup bagi jumlah produk catatan kelas dengan frekuensinya dengan jumlah total data:

$\displaystyle\overline{x}=\frac{\sum_{i=1}^N x_i\cdot f_i}{\sum_{i=1}^N f_i} =\frac{4985}{81}=61,54 \text{ kg}$

Sifat-sifat mean aritmatika

Rata-rata aritmatika memiliki ciri-ciri sebagai berikut:

Jumlah deviasi seluruh data dalam suatu distribusi dari mean menghasilkan nol.

$\sum_{i=1}^N\left(x_i-\overline{x}\right)=0$

Jika kita menambahkan jumlah yang sama ke semua data dalam sampel, rata-rata sampel bertambah sebesar jumlah tersebut.

Hal yang sama terjadi pada perkalian, jika semua nilai dalam sampel dikalikan dengan suatu angka, mean sampel dikalikan dengan angka tersebut.

Rata-rata aritmatika hanya dapat dihitung dalam variabel kuantitatif . Dengan kata lain, Anda tidak dapat mengambil rata-rata variabel kualitatif.

Rata-rata aritmatika akan selalu menjadi nilai antara minimum dan maksimum suatu distribusi.

$\text{min}\{x_1,x_2,...,x_N\}\leq \cfrac{x_1+\dots +x_N}{N}\leq \text{max}\{x_1,x_2,...,x_N\}$

Rata-rata jenis ini sangat sensitif terhadap nilai yang sangat tinggi atau sangat rendah sehingga menyebabkan outlier mengubah hasil rata-rata aritmatika secara signifikan.

Rata-rata aritmatika suatu kumpulan data selalu sama dengan atau lebih besar dari rata-rata geometrik kumpulan data yang sama.

$\displaystyle\frac{x_1+x_2+\dots+x_N}{N}\geq \sqrt[N]{x_1+x_2+\dots+x_N}$

Hitung mean aritmatika dengan Excel

Menghitung rata-rata aritmatika di Excel sangat sederhana, karena Anda hanya perlu memasukkan data pada lembar dan menggunakan fungsi AVERAGE .

Misalnya, untuk menentukan rata-rata aritmatika data dari latihan pertama yang kami jelaskan, cukup salin semua data ke dalam dokumen Excel dan tulis rumus berikut di dalam sel: =AVERAGE(9;7;5; 8;7 ,5) . Fungsi tersebut akan mengembalikan mean aritmatika data, yaitu 7.3.

Tentu saja, mencari rata-rata aritmatika suatu bilangan tertentu dengan program Excel jauh lebih cepat daripada menghitungnya dengan tangan, terutama bila ukuran sampelnya sangat besar.

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya