Artinya geometris

Oleh Benjamin anderson Agustus 6, 2023 Statistik 0 Komentar

Pada artikel ini kami akan menjelaskan apa itu mean geometrik, cara menghitungnya, dan apa perbedaan antara mean geometrik dan mean aritmatika. Anda juga akan dapat melihat latihan mean geometrik yang diselesaikan langkah demi langkah dan apa saja properti dari jenis mean ini. Terakhir, Anda akan menemukan kalkulator untuk menghitung rata-rata geometrik dari kumpulan data apa pun.

Apa yang dimaksud dengan geometri?

Rata-rata geometrik adalah ukuran sentralitas statistik deskriptif. Rata-rata geometrik sekumpulan data statistik sama dengan akar ke-n hasil perkalian semua nilai.

Rata-rata geometrik digunakan dalam keuangan bisnis untuk menghitung tingkat pengembalian, rata-rata persentase, dan bunga majemuk.

Oleh karena itu, rumus mean geometrik adalah sebagai berikut:

Rata-rata geometrik hanya dapat dihitung jika semua data dalam sampel bernilai positif. Karena jika suatu nilai negatif maka akarnya akan memiliki solusi negatif atau tidak ada solusi, sebaliknya jika suatu data nol maka perkalian datanya akan menghasilkan nol dan oleh karena itu rata-rata geometriknya akan sama dengan 0.

Rata-rata geometrik bukan satu-satunya jenis rata-rata yang ada, ada juga rata-rata aritmatika, rata-rata tertimbang, rata-rata kuadrat, dan rata-rata harmonik.

Perbedaan antara mean geometrik dan mean aritmatika

Perbedaan utama antara mean geometrik dan mean aritmatika adalah bahwa mean geometrik kurang sensitif terhadap nilai ekstrem dibandingkan mean aritmatika. Selain itu, mean aritmatika dapat dihitung dengan nilai negatif dan nol, sedangkan mean geometrik hanya dapat dihitung dengan nilai positif.

Demikian pula, rata-rata geometrik secara umum akan lebih rendah daripada rata-rata aritmatika untuk kumpulan data yang sama.

Perlu juga dicatat bahwa penghitungan rata-rata geometrik lebih kompleks dan oleh karena itu signifikansi statistiknya lebih sulit untuk diinterpretasikan.

Singkatnya, rata-rata geometri memiliki kelebihan dan kekurangan dibandingkan dengan rata-rata aritmatika dan, bergantung pada sifat datanya, akan tepat untuk menghitung rata-rata ini atau itu.

Cara menghitung mean geometrik

Untuk menghitung mean geometrik, langkah-langkah berikut harus dilakukan:

Hitung produk dari semua data statistik dalam sampel.
Temukan akar ke-n dari produk yang dihitung.
Hasil yang diperoleh adalah rata-rata geometrik sampel statistik.

Seperti yang Anda lihat, mencari rata-rata geometrik suatu kumpulan data relatif mudah menggunakan kalkulator atau program komputer, karena Anda hanya perlu menghitung hasil kali dan akar. Sebaliknya, menghitung dengan tangan cukup melelahkan.

👉 Inilah sebabnya kami menyarankan penggunaan kalkulator di bawah ini untuk menghitung rata-rata geometrik suatu kumpulan data.

Contoh Rata-Rata Geometris

Setelah kita melihat teori tentang mean geometrik, kita akan memberikan contohnya sehingga Anda dapat melihat dengan tepat cara mendapatkan mean geometrik.

Hasil ekonomi suatu perusahaan selama lima tahun terakhir diketahui. Pada tahun pertama perusahaan menghasilkan profitabilitas ekonomi sebesar 10%, pada tahun kedua laba mencapai 23%, pada tahun ketiga uang yang diperoleh sebesar 16%, pada tahun keempat mencapai profitabilitas ekonomi sebesar 7% dan investasi pada tahun kelima mewakili pengembalian sebesar 20%. Anda diminta menghitung rata-rata semua persentase.

Seperti yang telah kita ketahui, untuk menghitung rata-rata persentase sebaiknya tidak menggunakan rata-rata aritmatika, melainkan melakukan perhitungan dengan rata-rata geometri.

Oleh karena itu, kami menerapkan rumus rata-rata geometrik:

$MG=\sqrt[n]{\prod_{i=1}^Nx_i}=\sqrt[n]{x_1\cdot x_2\cdot \ldots x_n}$

Dan kami mengganti nilai contoh ke dalam rumus dan melakukan perhitungan:

$MG=\sqrt[5]{1,10\cdot 1,23\cdot 1,16\cdot 1,07\cdot 1,20}=1,15 \ \longrightarrow \ 15 \%$

Perhatikan bahwa kita memiliki lima titik data, jadi kita menghitung akar kelima.

Hasil numerik dari mean geometrik adalah 1,15 yang berarti perusahaan mengalami pertumbuhan ekonomi rata-rata 15% setiap tahunnya.

Ingatlah bahwa kami bisa mendapatkan rata-rata geometrik karena semua nilainya positif, tetapi jika ada persentase yang negatif, kami harus memasukkan data ke dalam rumus sebagai desimal positif dengan bagian bilangan bulat. sama dengan nol. Misalnya, pertumbuhan -30% harus dinyatakan dalam rumus sebagai 0,70 (1-0,3=0,7).

Kalkulator Rata-Rata Geometris

Masukkan statistik sampel apa pun ke dalam kalkulator di bawah ini untuk mencari rata-rata geometriknya. Data harus dipisahkan dengan spasi dan dimasukkan menggunakan titik sebagai pemisah desimal. Ingatlah bahwa Anda tidak dapat menentukan mean geometrik jika suatu nilai negatif atau nol.

Sifat-sifat mean geometrik

Rata-rata geometrik mempunyai ciri-ciri sebagai berikut:

Ini adalah jenis rata-rata yang sangat berguna untuk mencari rata-rata persentase atau indeks.

Itu hanya dapat dihitung jika semua datanya positif.

Arti geometri Rata-rata geometri dua bilangan a dan b adalah sisi-sisi persegi yang luasnya sama dengan persegi panjang yang sisi-sisinya berukuran a dan b .

$MG(a,b)=\sqrt{a\cdot b}$

Arti geometri dari rata-rata geometri tiga bilangan a , b dan c adalah sisi-sisi kubus yang volumenya setara dengan sisi-sisi sejajar a , b dan c .

$MG(a,b,c)=\sqrt[3]{a\cdot b \cdot c}$

Logaritma rata-rata geometri suatu kumpulan data memberikan rata-rata aritmatika dari logaritma kumpulan data yang sama.

Rata-rata geometrik suatu himpunan nilai akan selalu lebih kecil atau sama dengan rata-rata aritmatika.

$\sqrt[N]{x_1\cdot x_2\ldots x_N}\leq \cfrac{x_1+x_2+\ldots+x_N}{N}$

Rata-rata geometri tertimbang dihitung dengan cara yang sama seperti rata-rata geometrik, namun dengan menambahkan bobot pada eksponen setiap item data untuk memberi bobot pada nilai statistik.

$\displaystyle \left(\prod_{i=1}^n{x_i}^{\alpha_i}\right)^{\frac{1}{\sum_i{\alpha_i}}}= \left({x_1}^{\alpha_1}{x_2}^{\alpha_2}\dots{x_n}^{\alpha_n}\right)^{ \frac{1}{\alpha_1+ \dots+ \alpha_n}} \left}}$

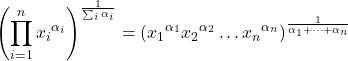
Hitung rata-rata geometrik di Excel

Terakhir, mari kita lihat cara mencari mean geometrik suatu kumpulan data menggunakan program Excel.

Untuk menghitung mean geometrik di Excel, Anda perlu menggunakan fungsi MEANS.GEOM. Cukup masukkan semua nilai yang ingin Anda ambil rata-rata geometrinya dan fungsi tersebut akan mengembalikan hasil rata-rata geometri.

Misalnya, untuk menentukan rata-rata geometrik dari contoh yang dikerjakan di atas, Anda harus menulis di kotak Excel =MEDIA.GEOM(1.1;1.23;1.16;1.07;1.20) .

Anda harus ingat bahwa jika salah satu nilainya nol atau negatif, fungsi akan mengembalikan kesalahan.

Seperti yang Anda lihat, menghitung rata-rata geometrik dengan Excel jauh lebih sederhana dan lebih cepat, karena Anda hanya perlu menyalin data ke lembar dan menggunakan rumus.

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya