Rata-rata harmonik

Berikut kami jelaskan apa itu mean harmonik dan cara menghitungnya (rumus). Selain itu, kami menghitung rata-rata harmonik dari sebuah contoh langkah demi langkah. Anda juga akan menemukan kalkulator untuk mengambil mean harmonik dari kumpulan data apa pun. Dan terakhir, Anda akan dapat melihat apa saja sifat-sifat mean harmonik.

Apa yang dimaksud dengan harmonik?

Rata-rata harmonik adalah ukuran posisi sentral statistik deskriptif. Rata-rata harmonik dihitung dengan membagi jumlah total data statistik dengan jumlah kebalikan dari setiap nilai.

Rata-rata harmonik digunakan untuk menghitung kecepatan rata-rata, waktu atau membuat perhitungan elektronik. Fitur ini membedakan rata-rata harmonik dari jenis rata-rata lainnya, yang sering digunakan dalam menghitung harga atau persentase rata-rata.

Jadi rumus mean harmoniknya adalah sebagai berikut:

Rata-rata harmonik biasanya dilambangkan dengan huruf kapital H.

Jenis rata-rata lain yang ada adalah rata-rata aritmatika, rata-rata tertimbang, rata-rata kuadrat, dan rata-rata geometri. Rata-rata harmonik memiliki kelebihan dan kekurangan dibandingkan dengan rata-rata jenis lainnya, berikut ini kita akan melihat apa saja itu.

Cara Menghitung Rata-Rata Harmonik

Untuk menghitung mean harmonik, langkah-langkah berikut harus dilakukan:

1. Hitung invers dari setiap data statistik dalam sampel.
2. Tambahkan semua invers terhitung.
3. Bagilah jumlah total data dengan jumlah yang ditemukan pada langkah sebelumnya.
4. Hasil yang diperoleh adalah mean harmonik sampel statistik.

👉 Seperti yang Anda lihat, mengambil mean harmonik dari suatu kumpulan data memerlukan banyak operasi, sehingga cukup melelahkan untuk melakukannya dengan tangan. Oleh karena itu, untuk menghitung mean harmonik, sebaiknya gunakan kalkulator di bawah ini.

Contoh mean harmonik

Setelah melihat teori tentang mean harmonik, kita akan melihat cara mencari mean harmonik dari sekumpulan data dengan menyelesaikan contoh langkah demi langkah harga suatu saham.

• Seseorang membeli saham suatu perusahaan setiap tahun selama 5 tahun berturut-turut. Selama periode ini, harga saham sangat berfluktuasi: pada tahun pertama setiap saham bernilai €7, pada tahun kedua €10, pada tahun ketiga €15, pada tahun keempat perusahaan mengalami kerugian finansial yang signifikan dan harga turun menjadi €6 per saham dan akhirnya, pada tahun kelima, perusahaan melakukan investasi besar yang menaikkan harga menjadi €11. Berapa harga rata-rata pembelian saham tersebut?

Salah satu pilihannya adalah menghitung rata-rata aritmatika, yaitu menjumlahkan semua harga dan membaginya dengan lima. Namun, karena pembelian dilakukan pada tahun yang berbeda, maka mengambil rata-rata aritmatika adalah suatu kesalahan. Oleh karena itu kita harus menemukan mean harmonik dari semua harga.

Selanjutnya kita terapkan rumus mean harmonik:

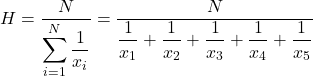
Dan kemudian kita mengganti nilai harga yang bermasalah ke dalam rumus dan menghitung mean harmonik:

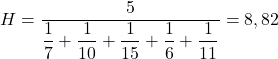
Anda harus membubuhkan lima pada pembilang pecahan karena ada lima informasi yang berbeda.

Oleh karena itu, harga rata-rata saham yang Anda beli selama periode ini adalah 8,82 euro per saham.

Kalkulator Rata-rata Harmonik

Dengan kalkulator berikut Anda dapat menghitung rata-rata harmonik dari kumpulan data statistik apa pun.

Anda harus memasukkan angka menggunakan titik sebagai pemisah desimal dan memisahkan angka dengan spasi. Ingatlah bahwa untuk mencari mean harmonik, tidak ada nilai yang boleh nol.

Sifat-sifat mean harmonik

Rata-rata harmonik mempunyai ciri-ciri sebagai berikut:

• Nilai yang besar mempunyai pengaruh yang kecil terhadap rata-rata harmonik suatu ansambel, artinya nilai yang sangat besar relatif terhadap data lain tidak akan menyebabkan perubahan nyata pada rata-rata harmonik.

• Di sisi lain, nilai yang kecil sangat mempengaruhi rata-rata harmonik suatu ansambel, sehingga mengurangi nilainya secara signifikan. Memang, kebalikan dari penyebut rumus tersebut kemudian mengambil nilai yang sangat besar.

• Rata-rata harmonik tidak dapat dihitung jika salah satu datanya nol, karena hal ini akan menyebabkan ketidakpastian dalam rumus. Dalam kasus seperti ini, mean harmonik dikatakan tidak terdefinisi.

• Kebalikan dari mean harmonik setara dengan mean aritmatika dari kebalikan observasi.

• Untuk kelompok data yang sama, mean harmonik akan lebih kecil atau sama dengan mean aritmatika.

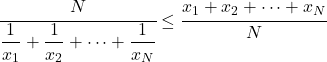
Hitung mean harmonik dengan Excel

Seperti yang telah kita lihat, menghitung mean harmonik secara manual bisa jadi sangat membosankan karena banyak perhitungan yang harus dilakukan. Dan menjadi lebih rumit lagi bila Anda memiliki data dalam jumlah besar. Oleh karena itu, untuk mencari mean harmonik, sebaiknya gunakan kalkulator atau program Excel.

Rata-rata harmonik di Excel dihitung dengan rumus MEAN.ARMO . Artinya, untuk menghitung rata-rata harmonik dari sekumpulan data, Anda perlu menyalinnya ke dalam lembar Excel dan memasukkan semua data ke dalam fungsi MEAN.ARMO .

Misalnya, untuk mendapatkan rata-rata harmonik dari latihan yang kita selesaikan di atas, tulislah di sel Excel =MEDIA.ARMO(7;10;15;6;11) .

Anda harus ingat bahwa jika salah satu nilainya nol, fungsi akan mengembalikan kesalahan, karena rata-rata harmonik dari sekumpulan nilai statistik tidak dapat ditentukan jika salah satu nilainya nol.