Rata-rata sampel

Oleh Benjamin anderson Agustus 3, 2023 Statistik 0 Komentar

Pada artikel ini Anda akan mengetahui berapa rata-rata sampel dalam statistik. Demikian pula, Anda akan menemukan cara menghitung rata-rata suatu sampel, latihan yang diselesaikan, dan, sebagai tambahan, kalkulator online untuk menghitung rata-rata sampel apa pun.

Apa yang dimaksud dengan sampel?

Dalam statistik, mean sampel adalah rata-rata dari nilai-nilai dalam suatu sampel. Untuk menghitung mean sampel, semua nilai dalam sampel harus dijumlahkan lalu dibagi dengan jumlah total data dalam sampel.

Simbol alat sampelnya adalah

$\overline{x}$

Dalam suatu penelitian statistik, umumnya tidak semua nilai suatu populasi diketahui, oleh karena itu dipilihlah sampel dari populasi untuk menganalisisnya dan mengekstrapolasi kesimpulan yang diperoleh ke seluruh populasi. Jadi, mean sampel digunakan untuk memperkirakan mean populasi.

Contoh Rumus Rata-Rata

Rata-rata sampel sama dengan jumlah seluruh nilai sampel dibagi dengan ukuran sampel. Artinya, untuk menghitung mean sampel, semua nilai dalam sampel dijumlahkan lalu dibagi dengan jumlah total data dalam sampel.

Oleh karena itu, rumus untuk menghitung mean sampel adalah:

$\displaystyle\overline{x}=\frac{\displaystyle \sum_{i=1}^n x_i}{n}=\frac{x_1+x_2+\dots +x_n}{n}$

👉 Anda dapat menggunakan kalkulator di bawah ini untuk menghitung mean sampel dari kumpulan data apa pun.

Perlu diingat bahwa mean sampel dihitung menggunakan data dari suatu sampel, sehingga nilai mean populasi mungkin berbeda dengan nilai yang dihitung.

Contoh Contoh Perhitungan Mean

Sekarang setelah kita mengetahui definisi mean sampel dan rumusnya, mari kita lihat cara mendapatkan mean sampel dari suatu kumpulan data dengan menyelesaikan contoh sederhana.

Jose ingin pindah ke pusat kota, tapi dia tidak punya banyak waktu sehingga dia tidak bisa menganalisa harga semua apartemen yang disewakan. Jadi Anda memutuskan untuk hanya melihat harga sewa lima apartemen (ditampilkan di bawah) untuk mengetahui berapa biaya yang Anda keluarkan untuk tinggal di pusat kota. Berapa harga rata-rata sampel tersebut?

€600 €430 €820 €575 €950

Untuk mencari mean sampel, kita perlu menjumlahkan semua nilai sampel lalu membaginya dengan jumlah observasi, yaitu 5. Jadi, kita terapkan rumus mean sampel:

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^n x_i}{n}=\frac{x_1+x_2+x_3+x_4+x_5}{n}$

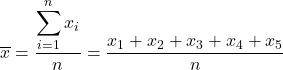
Selanjutnya, kita substitusikan data ke dalam rumus dan hitung mean sampel:

$\overline{x}=\cfrac{600+430+820+575+950}{5}=675$

Singkatnya, harga rata-rata sampel apartemen yang dipilih untuk sampel adalah €675.

Contoh Kalkulator Rata-rata

Masukkan data dari sampel statistik apa pun ke dalam kalkulator berikut untuk menghitung rata-rata sampelnya. Data harus dipisahkan dengan spasi dan dimasukkan menggunakan titik sebagai pemisah desimal.

Rata-rata sampel dan rata-rata populasi

Rata-rata populasi adalah rata-rata dari populasi statistik . Oleh karena itu, rata-rata populasi adalah rata-rata dari semua elemen yang ingin dilakukan studi statistik.

Oleh karena itu, perbedaan antara mean sampel dan mean populasi adalah mean sampel adalah rata-rata dari nilai-nilai sampel, sedangkan mean populasi adalah rata-rata dari nilai-nilai dalam populasi.

Untuk membedakan mean sampel dari mean populasi, keduanya diwakili oleh simbol yang berbeda. Simbol alat sampelnya adalah

$\overline{x}$

, sedangkan lambang penduduk artinya adalah

$\mu$

$\begin{array}{c}\overline{x} = \text{Media muestral}\\[2ex]\mu =\text{Media poblacional}\end{array}$

Rata-rata sampel digunakan untuk memperkirakan nilai rata-rata populasi, yang dapat dilakukan dengan menggunakan estimasi titik atau estimasi interval .

➤ Lihat: Berapa rata-rata populasinya?

Distribusi pengambilan sampel rata-rata sampel

Terakhir, mari kita lihat apa yang dimaksud dengan distribusi sampling dari sampel, karena ini merupakan konsep statistik yang dapat membingungkan.

Pertama, mari kita mulai dengan mendefinisikan apa itu distribusi sampling. Distribusi sampling adalah distribusi yang dihasilkan dengan memperhitungkan semua kemungkinan sampel dari suatu populasi statistik.

Oleh karena itu, distribusi sampling dari mean sampel adalah distribusi yang dihasilkan dari penghitungan mean setiap kemungkinan sampel dari suatu populasi. Artinya, jika kita mempelajari semua kemungkinan sampel dari suatu populasi dan menghitung rata-rata setiap sampel, himpunan nilai yang dihitung adalah distribusi pengambilan sampel dari rata-rata sampel.

Kesimpulannya, walaupun mean sampel dan distribusi sampling memiliki nama yang mirip, namun perlu diketahui cara membedakannya: mean sampel adalah parameter statistik yang dihitung dari suatu sampel, sebaliknya distribusi sampling adalah distribusi. yang dihasilkan dari mempelajari semua sampel yang dapat diambil dari suatu populasi.

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya