Rata-rata tertimbang

Oleh Benjamin anderson Agustus 6, 2023 Statistik 0 Komentar

Di sini kami menjelaskan apa itu rata-rata tertimbang dan cara menghitungnya. Anda akan dapat melihat latihan terselesaikan tentang cara kami menemukan rata-rata tertimbang. Dan terlebih lagi, Anda dapat menghitung rata-rata tertimbang dari setiap kumpulan data dengan kalkulator di bagian akhir.

Berapa rata-rata tertimbangnya?

Rata-rata tertimbang adalah ukuran sentralitas statistik deskriptif. Untuk menghitung rata-rata tertimbang, pertama-tama Anda harus mengalikan setiap data statistik dengan bobotnya (atau bobotnya), lalu menjumlahkan semua hasil kali, dan terakhir membagi jumlah tertimbang dengan jumlah semua bobot.

Dengan kata lain rumus rata-rata tertimbang adalah sebagai berikut:

Dimana x _i mewakili setiap sampel data dan w _i bobotnya yang sesuai.

Jadi, semakin besar bobot suatu data, semakin penting data tersebut dalam penghitungan rata-rata tertimbang. Dengan kata lain, semakin tinggi bobot suatu data, maka akan semakin besar pengaruhnya terhadap hasil rata-rata tertimbang.

Rata-rata tertimbang sangat berguna untuk menghitung nilai, karena memungkinkan Anda mengevaluasi latihan atau ujian yang diambil selama kursus dengan tingkat kepentingan yang berbeda-beda. Rata-rata tertimbang juga digunakan untuk menghitung CPI (Indeks Harga Konsumen), yang merupakan indikator untuk mengukur harga suatu populasi.

Selain rata-rata tertimbang, terdapat juga jenis rata-rata lainnya seperti rata-rata geometri, rata-rata aritmatika, rata-rata kuadrat, dan rata-rata harmonik.

Cara menghitung rata-rata tertimbang

Untuk menghitung rata-rata tertimbang, langkah-langkah berikut harus diikuti:

Kalikan setiap data statistik dengan bobotnya yang sesuai.
Jumlahkan semua produk yang dihitung pada langkah sebelumnya.
Bagilah jumlah bobot di atas dengan jumlah seluruh bobot.
Hasil yang diperoleh adalah rata-rata tertimbang dari sampel statistik.

👉 Anda dapat menggunakan kalkulator di bawah ini untuk menghitung rata-rata tertimbang dari kumpulan data apa pun.

Contoh Rata-Rata Tertimbang

Mempertimbangkan definisi rata-rata tertimbang, sekarang kita akan menyelesaikan latihan untuk memahami sepenuhnya bagaimana rata-rata tertimbang diperoleh dari sekumpulan data.

Seorang siswa SMA tahun pertama memperoleh nilai sebagai berikut dalam mata pelajaran matematika: nilai 7 pada ujian parsial yang dihitung 30%, nilai 9 pada kerja kelompok yang bernilai 20%, nilai 6 pada latihan yang diberikan di kelas dengan pembobotan. sebesar 10% dan nilai 8 pada ujian akhir yang mempunyai bobot 40%. Berapa nilai akhir Anda untuk mata pelajaran tersebut?

Untuk menentukan nilai siswa, Anda harus mencari rata-rata tertimbang dengan nilai yang diberikan oleh pernyataan tersebut. Untuk melakukan ini, kami menerapkan rumus rata-rata tertimbang:

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+x_3\cdot w_3+x_4\cdot w_4+x_5\cdot w_5}{w_1+w_2+w_3+w_4+w_5}$

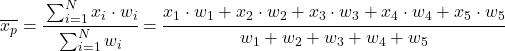
Skor setiap penyampaian merupakan nilai statistik dan persentasenya sesuai dengan bobot nilai tersebut. Oleh karena itu, kami mengganti nilai dan bobot ke dalam rumus dan melakukan perhitungan rata-rata tertimbang:

$\overline{x_p}=\cfrac{7\cdot 0,30+9\cdot 0,20+6\cdot 0,10+8\cdot 0,40}{0,30+0,20+0,10+0,40}=7,7$

Jadi nilai akhir matematika siswa tersebut adalah 7,7 karena ini merupakan hasil yang diperoleh dari rata-rata tertimbang.

Kalkulator Rata-Rata Tertimbang

Masukkan data dari sampel statistik apa pun dan bobotnya masing-masing ke dalam kalkulator di bawah ini untuk menghitung rata-rata tertimbangnya.

Masukkan data statistik pada kotak pertama dan bobotnya masing-masing pada kotak kedua. Anda harus menuliskan bobot dalam urutan yang sama dengan data dan dalam format desimal. Semua angka harus dipisahkan dengan spasi dan dimasukkan menggunakan titik sebagai pemisah desimal.

Anak timbang yang terstandarisasi

Seperti yang telah kita lihat, dalam rata-rata tertimbang, bobot adalah nilai yang diberikan pada setiap bagian data agar lebih atau kurang penting. Jadi, jika suatu informasi sangat penting maka bobotnya akan sangat tinggi, namun jika informasinya tidak terlalu relevan maka bobotnya akan sangat rendah.

Nah, bobot ternormalisasi adalah jenis pembobotan yang digunakan untuk mendapatkan rata-rata tertimbang tanpa harus melakukan pembagian apa pun.

Bobot yang dinormalisasi adalah bobot suatu item data dibagi dengan jumlah seluruh bobot.

$w_i'=\cfrac{w_i}{\sum_{k=1}^N w_k}$

Oleh karena itu, jumlah semua bobot yang dinormalisasi sama dengan satu:

$\sum_{i=1}^N w_i'=1$

Jadi, untuk menghitung rata-rata tertimbang dengan bobot yang dinormalisasi , cukup kalikan setiap item data dengan bobot yang dinormalisasi:

$\displaystyle\overline{x_p}=\sum_{i=1}^N x_i\cdot w_i'=x_1\cdot w_1'+x_2\cdot w_2'+\dots+x_N\cdot w_N'$

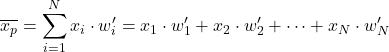
Misalnya kita mempunyai sampel statistik yang datanya 24, 35, 17, 41 dan bobotnya masing-masing adalah 4, 9, 6, 3. Untuk mencari rata-rata tertimbang dari kumpulan data ini, pertama-tama kita dapat menghitung bobot yang dinormalisasi dengan membagi setiap bobot dengan jumlah semua bobot:

$\cfrac{4}{4+9+6+3}=0,18$

$\cfrac{9}{4+9+6+3}=0,41$

$\cfrac{6}{4+9+6+3}=0,27$

$\cfrac{3}{4+9+6+3}=0,14$

Dan sekarang kalikan saja setiap data dengan bobot normalisasinya dan hasilnya akan menjadi rata-rata tertimbang:

$\overline{x_p}=24\cdot 0,18+35\cdot 0,41+17\cdot 0,27+41\cdot 0,14=28,91$

Perbedaan antara rata-rata tertimbang dan rata-rata aritmatika

Perhitungan rata-rata tertimbang dan rata-rata aritmatika dilakukan dengan cara yang sama, karena operasi serupa harus dilakukan. Dalam rata-rata tertimbang, setiap titik data dikalikan dengan bobotnya dan dibagi dengan jumlah bobotnya, namun dalam rata-rata aritmatika, semua data dijumlahkan dan dibagi dengan jumlah total titik data.

Perbedaan rata-rata tertimbang dan rata-rata aritmatika terletak pada konsepnya, karena pada rata-rata aritmatika dianggap semua data mempunyai nilai yang sama, namun pada rata-rata tertimbang setiap data mempunyai bobot yang berbeda.

Perhatikan bahwa jika semua bobot sama, maka rata-rata tertimbang setara dengan rata-rata aritmatika. Anda dapat melihat bukti matematisnya di bawah ini:

$\begin{aligned}\overline{x_p}&=\cfrac{x_1\cdot w+x_2\cdot w+x_3\cdot w+\dots+x_N\cdot w}{w+w+w+\dots +w}\\[2ex]&= \cfrac{w\cdot (x_1+x_2+\dots+x_N)}{N\cdot w}=\\[2ex] &= \cfrac{x_1+x_2+\dots+x_N}{N}=\overline{x}\end{aligned}$

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya