Regresi melalui titik asal: definisi & contoh

Regresi linier sederhana adalah metode yang dapat digunakan untuk mengukur hubungan antara satu atau lebih variabel prediktor dan variabel respon .

Model regresi linier sederhana memiliki bentuk sebagai berikut:

kamu = β ₀ + β ₁ x

Emas:

• y : Nilai variabel respon
• β ₀ : Nilai variabel respon ketika x = 0 (disebut istilah “intersep”)
• β ₁ : Rata-rata kenaikan variabel respon yang berhubungan dengan kenaikan satu satuan x
• x : Nilai variabel prediktif

Versi modifikasi dari model ini dikenal sebagai regresi melalui titik asal , yang memaksa y sama dengan 0 ketika x sama dengan 0.

Model jenis ini mengambil bentuk sebagai berikut:

kamu = _β1x

Perhatikan bahwa istilah intersep telah dihapus seluruhnya dari model.

Model ini terkadang digunakan ketika peneliti mengetahui bahwa variabel respon harus nol padahal variabel prediktornya nol.

Di dunia nyata, model jenis ini paling sering digunakan dalam studi kehutanan atau ekologi .

Misalnya, peneliti dapat menggunakan keliling pohon untuk memperkirakan tinggi pohon. Jika suatu pohon mempunyai keliling nol, maka tingginya juga harus nol.

Jadi, ketika menyesuaikan model regresi dengan data ini, tidak masuk akal jika suku aslinya bukan nol.

Contoh berikut menunjukkan perbedaan antara pemasangan model regresi linier sederhana biasa dan model yang menerapkan regresi melalui titik asal.

Contoh: regresi melalui titik asal

Misalkan seorang ahli biologi ingin menyesuaikan model regresi menggunakan keliling pohon untuk memprediksi tinggi pohon. Dia keluar dan mengumpulkan pengukuran berikut untuk sampel 15 pohon:

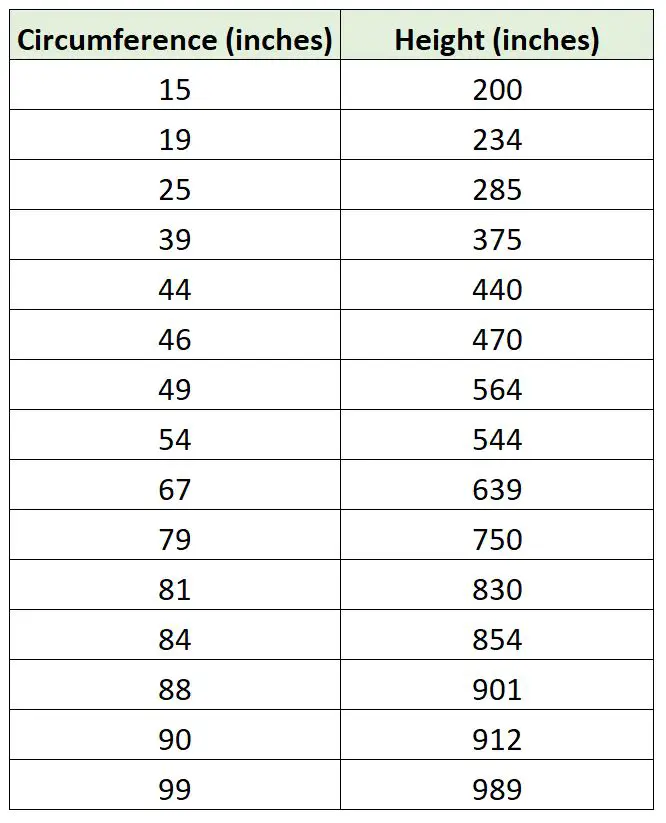
Kita dapat menggunakan kode berikut di R untuk menyesuaikan model regresi linier sederhana dengan model regresi yang tidak menggunakan intersep dan memplot dua garis regresi:

 #create data frame
df <- data. frame (circ=c(15, 19, 25, 39, 44, 46, 49, 54, 67, 79, 81, 84, 88, 90, 99),
                 height=c(200, 234, 285, 375, 440, 470, 564, 544, 639, 750, 830, 854,
                          901, 912, 989))

#fit a simple linear regression model
model <- lm(height ~ circ, data = df)

#fit regression through the origin
model_origin <- lm(height ~ 0 + ., data = df)

#create scatterplot
plot(df$circ, df$height, xlab=' Circumference ', ylab=' Height ',
     cex= 1.5 , pch= 16 , ylim=c(0.1000), xlim=c(0.100))

#add the fitted regression lines to the scatterplot
abline(model, col=' blue ', lwd= 2 )
abline(model_origin, lty=' dashed ', col=' red ', lwd= 2 )

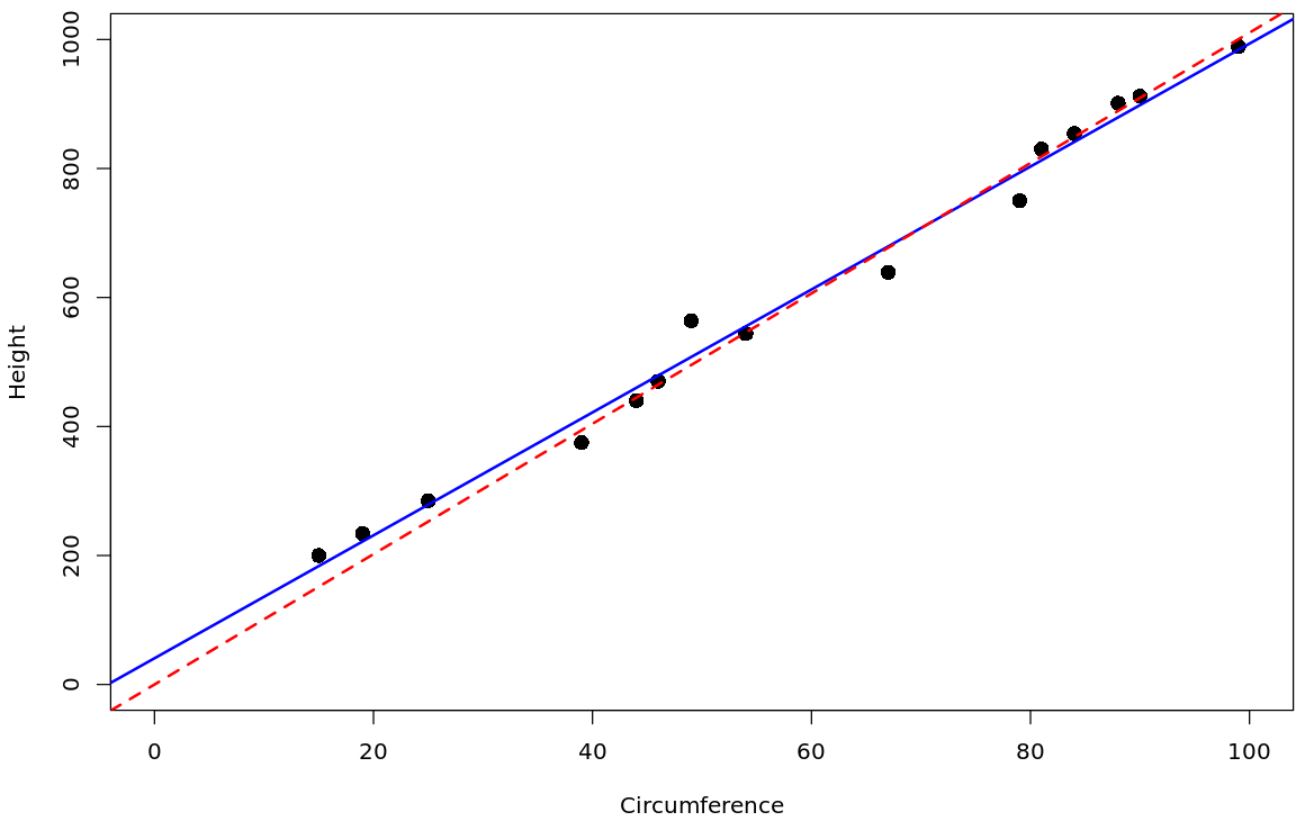
Garis putus-putus berwarna merah melambangkan model regresi yang melewati titik asal, dan garis padat berwarna biru melambangkan model regresi linier sederhana biasa.

Kita dapat menggunakan kode berikut di R untuk mendapatkan estimasi koefisien untuk setiap model:

 #display coefficients for simple linear regression model
coef(model)

(Intercept) circ 
  40.696971 9.529631 

#display coefficients for regression model through the origin
coef(model_origin)

    circ 
10.10574 

Persamaan yang cocok untuk model regresi linier sederhana adalah:

Tinggi = 40,6969 + 9,5296 (keliling)

Dan persamaan yang cocok untuk model regresi melalui titik asal adalah:

Tinggi = 10,1057 (keliling)

Perhatikan bahwa estimasi koefisien untuk variabel keliling sedikit berbeda.

Tindakan Pencegahan dalam Menggunakan Regresi melalui Asal

Sebelum menggunakan regresi intersep, Anda harus benar-benar yakin bahwa nilai 0 untuk variabel prediktor berarti nilai 0 untuk variabel respon. Dalam banyak skenario, hampir mustahil untuk mengetahui secara pasti.

Dan jika Anda menggunakan regresi melalui titik asal untuk menjaga kebebasan dalam memperkirakan titik asal, hal ini jarang menimbulkan perbedaan besar jika ukuran sampel Anda cukup besar.

Jika Anda memilih untuk menggunakan regresi melalui titik asal, pastikan untuk menguraikan alasan Anda dalam analisis atau laporan akhir Anda.

Sumber daya tambahan

Tutorial berikut memberikan informasi tambahan tentang regresi linier:

Pengantar Regresi Linier Sederhana
Pengantar Regresi Linier Berganda
Cara Membaca dan Menafsirkan Tabel Regresi