Bagaimana melakukan regresi kuadrat di r

Ketika dua variabel memiliki hubungan linier, kita sering kali dapat menggunakan regresi linier sederhana untuk mengukur hubungan keduanya.

Namun, jika dua variabel mempunyai hubungan kuadrat, kita dapat menggunakan regresi kuadrat untuk mengukur hubungannya.

Tutorial ini menjelaskan cara melakukan regresi kuadrat di R.

Contoh: regresi kuadratik di R

Misalkan kita ingin memahami hubungan antara jumlah jam kerja dan kebahagiaan yang dilaporkan. Kami memiliki data berikut mengenai jumlah jam kerja per minggu dan tingkat kebahagiaan yang dilaporkan (dalam skala 0 hingga 100) untuk 11 orang berbeda:

Gunakan langkah-langkah berikut untuk menyesuaikan model regresi kuadrat di R.

Langkah 1: Masukkan datanya.

Pertama, kita akan membuat bingkai data yang berisi data kita:

 #createdata
data <- data.frame(hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                   happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))

#viewdata 
data

   hours happiness
1 6 14
2 9 28
3 12 50
4 14 70
5 30 89
6 35 94
7 40 90
8 47 75
9 51 59
10 55 44
11 60 27

Langkah 2: Visualisasikan datanya.

Selanjutnya kita akan membuat scatterplot sederhana untuk memvisualisasikan data.

 #create scatterplot
plot(data$hours, data$happiness, pch=16) 

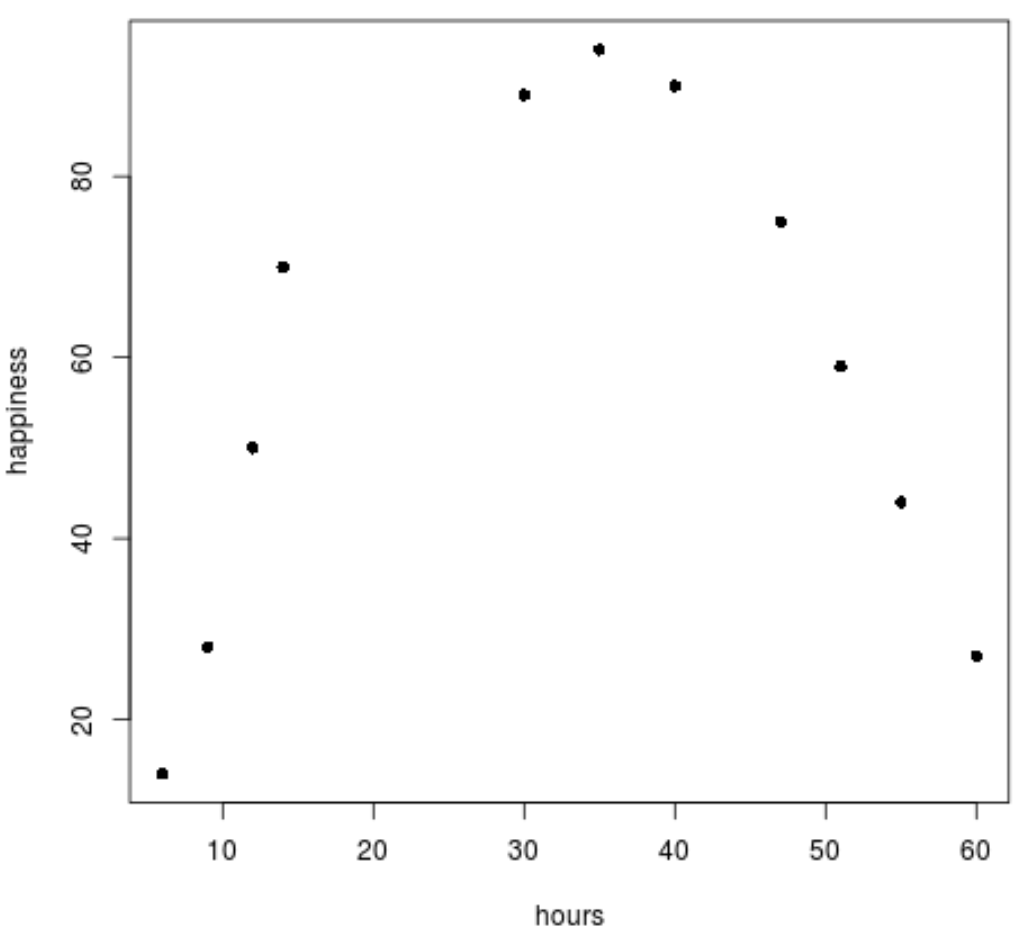
Kita dapat melihat dengan jelas bahwa data tidak mengikuti pola linier.

Langkah 3: Sesuaikan model regresi linier sederhana.

Selanjutnya, kita akan menyesuaikan model regresi linier sederhana untuk melihat seberapa cocok model tersebut dengan data:

 #fit linear model
linearModel <- lm(happiness ~ hours, data=data)

#view model summary
summary(linearModel)

Call:
lm(formula = happiness ~ hours)

Residuals:
   Min 1Q Median 3Q Max 
-39.34 -21.99 -2.03 23.50 35.11 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept) 48.4531 17.3288 2.796 0.0208 *
hours 0.2981 0.4599 0.648 0.5331  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 28.72 on 9 degrees of freedom
Multiple R-squared: 0.0446, Adjusted R-squared: -0.06156 
F-statistic: 0.4201 on 1 and 9 DF, p-value: 0.5331

Total varians kebahagiaan yang dijelaskan oleh model hanya sebesar 4,46% yang ditunjukkan oleh nilai multiple R-squared.

Langkah 4: Sesuaikan model regresi kuadrat.

Selanjutnya, kita akan menyesuaikan model regresi kuadratik.

 #create a new variable for hours 2
data$hours2 <- data$hours^2

#fit quadratic regression model
quadraticModel <- lm(happiness ~ hours + hours2, data=data)

#view model summary
summary(quadraticModel)

Call:
lm(formula = happiness ~ hours + hours2, data = data)

Residuals:
    Min 1Q Median 3Q Max 
-6.2484 -3.7429 -0.1812 1.1464 13.6678 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -18.25364 6.18507 -2.951 0.0184 *  
hours 6.74436 0.48551 13.891 6.98e-07 ***
hours2 -0.10120 0.00746 -13.565 8.38e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.218 on 8 degrees of freedom
Multiple R-squared: 0.9602, Adjusted R-squared: 0.9502 
F-statistic: 96.49 on 2 and 8 DF, p-value: 2.51e-06

Total varian kebahagiaan yang dijelaskan oleh model meningkat menjadi 96,02% .

Kita dapat menggunakan kode berikut untuk memvisualisasikan seberapa cocok model dengan data:

 #create sequence of hour values
hourValues <- seq(0, 60, 0.1)

#create list of predicted happiness levels using quadratic model
happinessPredict <- predict(quadraticModel, list(hours=hourValues, hours2=hourValues^2))

#create scatterplot of original data values
plot(data$hours, data$happiness, pch=16)
#add predicted lines based on quadratic regression model
lines(hourValues, happinessPredict, col='blue')

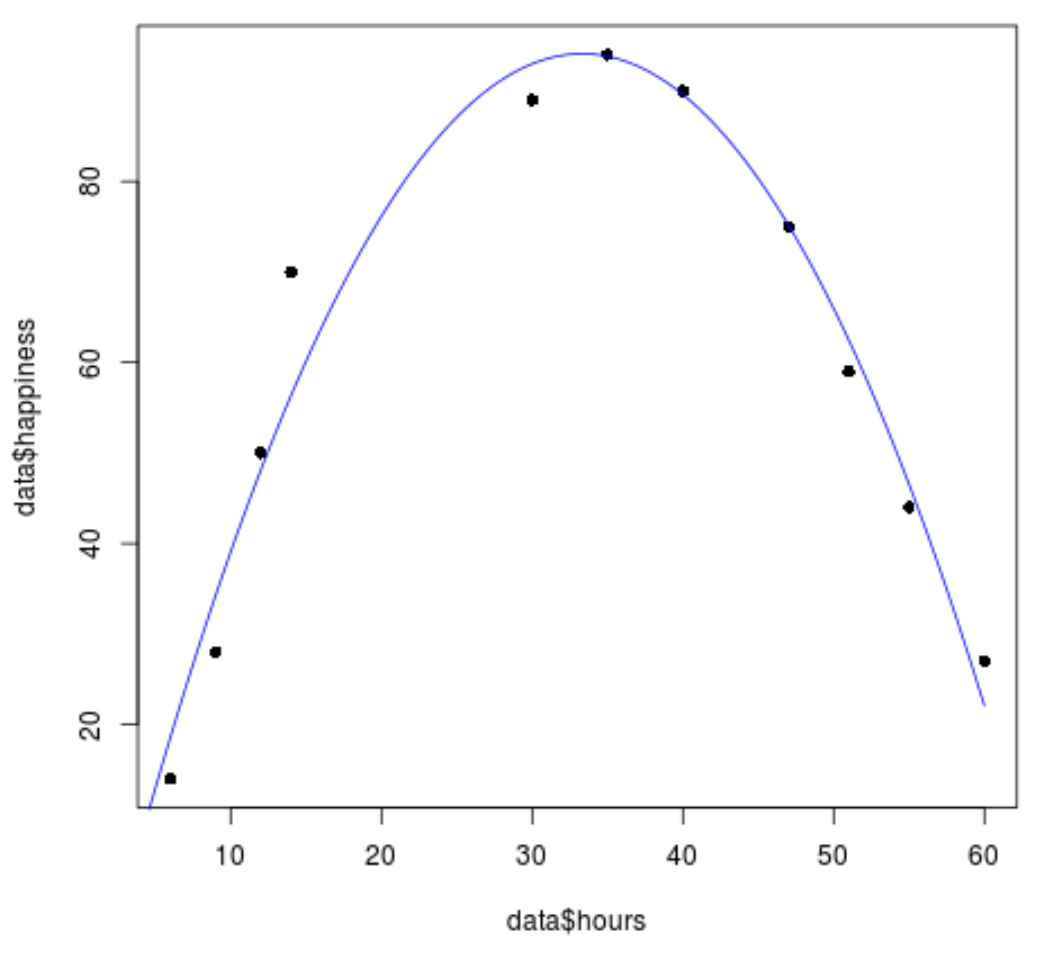
Kita dapat melihat bahwa garis regresi kuadrat cukup sesuai dengan nilai data.

Langkah 5: Tafsirkan model regresi kuadratik.

Pada langkah sebelumnya kita melihat bahwa hasil model regresi kuadrat adalah:

 Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -18.25364 6.18507 -2.951 0.0184 *  
hours 6.74436 0.48551 13.891 6.98e-07 ***
hours2 -0.10120 0.00746 -13.565 8.38e-07 ***

Berdasarkan koefisien yang disajikan di sini, regresi kuadrat yang disesuaikan adalah:

Kebahagiaan = -0,1012 (jam) ² + 6,7444 (jam) – 18,2536

Kita dapat menggunakan persamaan ini untuk mengetahui prediksi kebahagiaan seseorang, berdasarkan jumlah jam kerja mereka per minggu.

Misalnya seseorang yang bekerja 60 jam per minggu akan memiliki tingkat kebahagiaan 22,09 :

Kebahagiaan = -0,1012(60) ² + 6,7444(60) – 18,2536 = 22,09

Sebaliknya, seseorang yang bekerja 30 jam per minggu seharusnya memiliki tingkat kebahagiaan 92,99 :

Kebahagiaan = -0,1012(30) ² + 6,7444(30) – 18,2536 = 92,99