Bagaimana melakukan regresi kuantil di r

Regresi linier merupakan metode yang dapat kita gunakan untuk memahami hubungan antara satu atau lebih variabel prediktor dan variabel respon .

Biasanya, saat kita melakukan regresi linier, kita ingin memperkirakan nilai rata-rata variabel respon.

Namun, kita dapat menggunakan metode yang disebut regresi kuantil untuk memperkirakan nilai kuantil atau persentil dari nilai respons, seperti persentil ke-70, persentil ke-90, persentil ke-98, dan sebagainya.

Untuk melakukan regresi kuantil di R, kita dapat menggunakan fungsi rq() dari paket quantreg , yang menggunakan sintaks berikut:

 library (quantreg)

model <- rq(y ~ x, data = dataset, tau = 0.5 )

Emas:

• y : variabel respon
• x: variabel prediktif
• data: nama kumpulan data
• tau : Persentil yang ditemukan. Standarnya adalah median (tau = 0,5), namun Anda dapat mengaturnya ke angka apa pun antara 0 dan 1.

Tutorial ini memberikan contoh langkah demi langkah tentang cara menggunakan fungsi ini untuk melakukan regresi kuantil di R.

Langkah 1: Masukkan datanya

Untuk contoh ini, kami akan membuat kumpulan data yang berisi jam belajar dan hasil ujian yang diperoleh untuk 100 mahasiswa berbeda di sebuah universitas:

 #make this example reproducible
set.seed(0)

#create data frame 
hours <- runif(100, 1, 10)
score <- 60 + 2*hours + rnorm(100, mean=0, sd=.45*hours)
df <- data.frame(hours, score)

#view first six rows
head(df)

     hours score
1 9.070275 79.22682
2 3.389578 66.20457
3 4.349115 73.47623
4 6.155680 70.10823
5 9.173870 78.12119
6 2.815137 65.94716

Langkah 2: Lakukan Regresi Kuantil

Selanjutnya, kita akan menyesuaikan model regresi kuantil dengan menggunakan jam belajar sebagai variabel prediktor dan nilai ujian sebagai variabel respon.

Kami akan menggunakan model tersebut untuk memprediksi perkiraan nilai ujian persentil ke-90 berdasarkan jumlah jam belajar:

 library (quantreg)

#fit model
model <- rq(score ~ hours, data = df, tau = 0.9 )

#view summary of model
summary(model)

Call: rq(formula = score ~ hours, tau = 0.9, data = df)

tau: [1] 0.9

Coefficients:
            coefficients lower bd upper bd
(Intercept) 60.25185 59.27193 62.56459
hours 2.43746 1.98094 2.76989

Dari hasilnya kita dapat melihat persamaan regresi estimasi:

Nilai ujian persentil ke-90 = 60,25 + 2,437*(jam)

Misalnya, nilai persentil ke-90 untuk seluruh siswa yang belajar 8 jam seharusnya adalah 79,75:

Persentil ke-90 nilai ujian = 60,25 + 2,437*(8) = 79,75 .

Outputnya juga menampilkan batas kepercayaan atas dan bawah untuk intersep dan waktu variabel prediktor.

Langkah 3: Visualisasikan hasilnya

Kita juga dapat memvisualisasikan hasil regresi dengan membuat plot sebar dengan persamaan regresi kuantil yang dilapiskan pada grafik:

 library (ggplot2)

#create scatterplot with quantile regression line
ggplot(df, aes(hours,score)) +
  geom_point() + 
  geom_abline(intercept= coef (model)[1], slope= coef (model)[2]) 

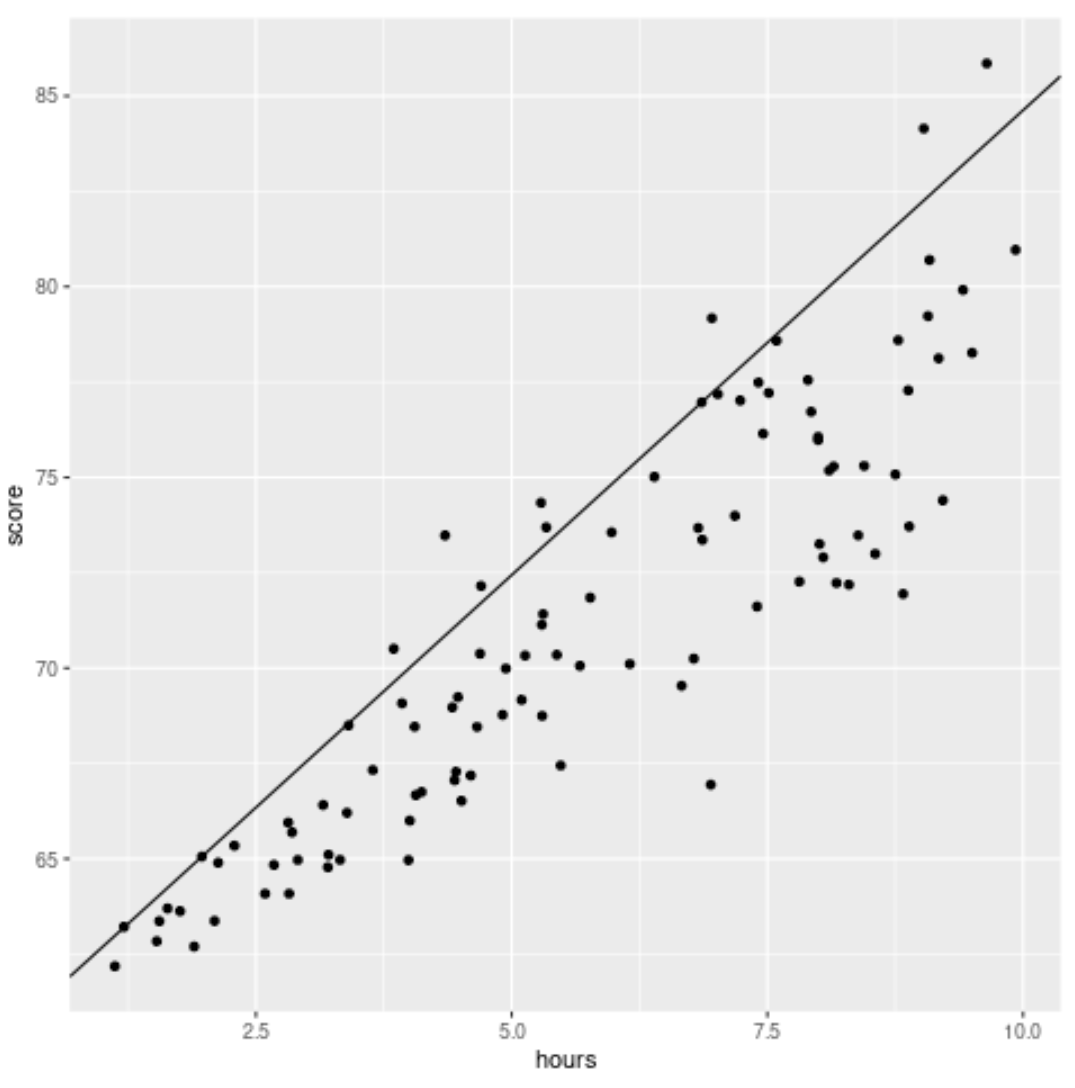
Berbeda dengan garis regresi linier tradisional, perhatikan bahwa garis yang dipasang ini tidak melewati inti data. Sebaliknya, ia melewati perkiraan persentil ke-90 pada setiap tingkat variabel prediktor.

Kita dapat melihat perbedaan antara persamaan regresi kuantil pas dan persamaan regresi linier sederhana dengan menambahkan argumen geom_smooth() :

 library (ggplot2)

#create scatterplot with quantile regression line and simple linear regression line
ggplot(df, aes(hours,score)) +
  geom_point() + 
  geom_abline(intercept= coef (model)[1], slope= coef (model)[2]) +
  geom_smooth(method=" lm ", se= F ) 

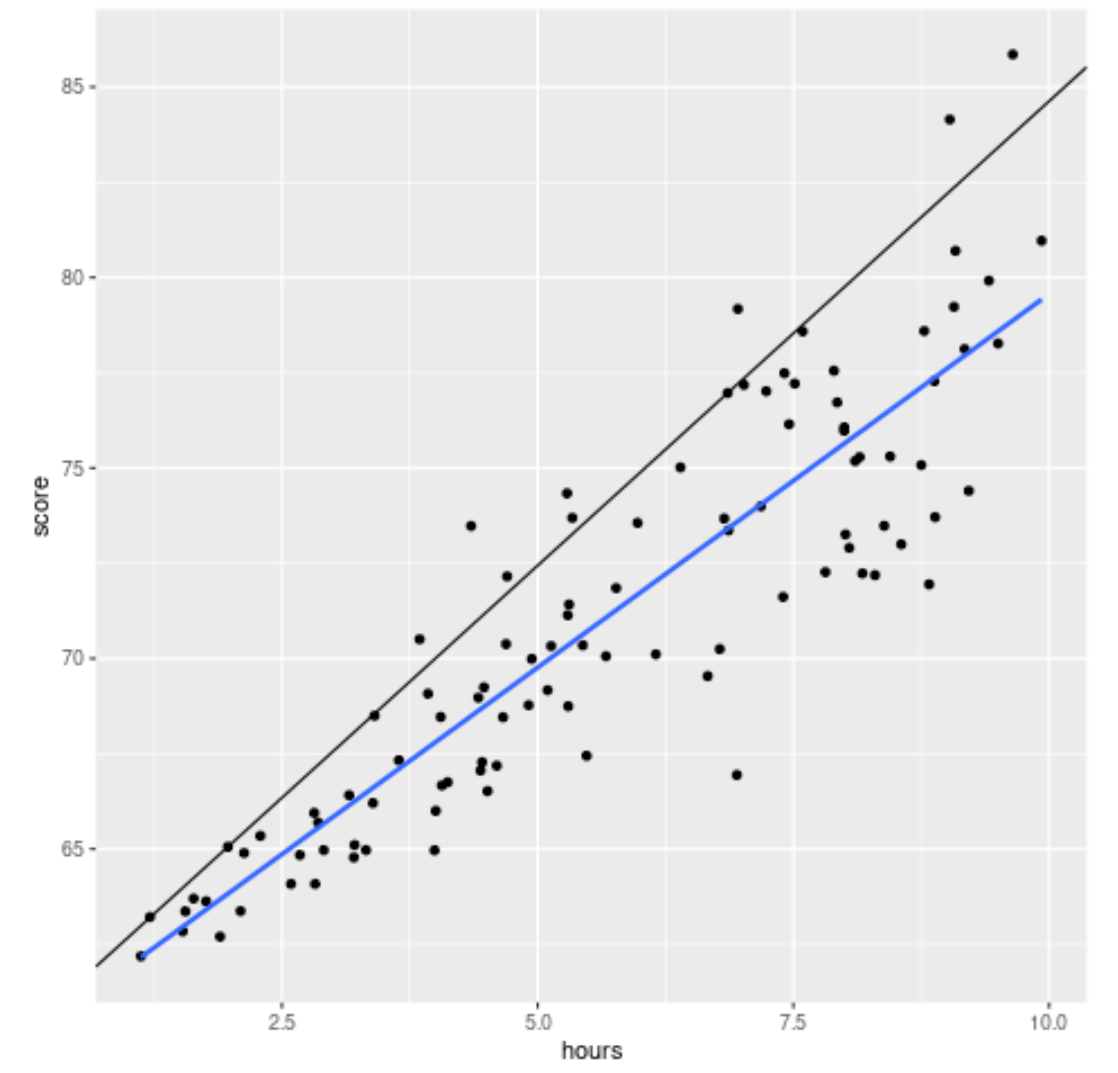
Garis hitam menampilkan garis regresi kuantil yang disesuaikan dengan persentil ke-90 dan garis biru menampilkan garis regresi linier sederhana yang memperkirakan nilai rata-rata variabel respon.

Seperti yang diharapkan, garis regresi linier sederhana menelusuri data dan menunjukkan perkiraan nilai rata-rata nilai ujian pada setiap tingkat jam.

Sumber daya tambahan

Tutorial berikut menjelaskan cara melakukan tugas umum lainnya di R:

Cara melakukan regresi linier sederhana di R
Cara melakukan regresi linier berganda di R
Bagaimana melakukan regresi kuadrat di R