Cara melakukan regresi bertahap di sas (dengan contoh)

Regresi bertahap adalah prosedur yang dapat kita gunakan untuk membangun model regresi dari sekumpulan variabel prediktor dengan memasukkan dan menghapus prediktor secara bertahap ke dalam model hingga tidak ada lagi alasan yang valid secara statistik untuk memasukkan atau hapus lebih banyak.

Tujuan dari regresi bertahap adalah untuk membuat model regresi yang mencakup semua variabel prediktor yang secara statistik berhubungan signifikan dengan variabel respon .

Untuk melakukan regresi bertahap di SAS, Anda dapat menggunakan PROC REG dengan pernyataan SELECTION .

Contoh berikut menunjukkan cara melakukan regresi bertahap di SAS dalam praktiknya.

Contoh: Melakukan Regresi Langkah demi Langkah di SAS

Misalkan kita memiliki kumpulan data berikut di SAS yang berisi empat variabel prediktor (x1, x2, x3, x4) dan satu variabel respons (y):

 /*create dataset*/
data my_data;
    input x1 x2 x3 x4 y;
    datalines ;
1 4 10 13 78
2 4 12 14 81
5 3 7 10 75
8 2 13 9 97
10 5 12 5 95
14 7 8 6 90
17 8 10 6 86 
19 5 15 5 90
20 5 12 4 93
21 4 10 3 95
;
run ;

/*view dataset*/
proc print data =my_data;

Sekarang misalkan kita ingin menentukan kombinasi variabel prediktor mana yang akan menghasilkan model regresi linier berganda terbaik.

Ketika kita berbicara tentang model regresi “terbaik”, yang kita maksud adalah model yang memaksimalkan atau meminimalkan ukuran tertentu.

Ada dua metrik yang biasa kami gunakan untuk mengevaluasi model regresi mana yang terbaik di antara sekelompok model potensial:

1. R-squared yang disesuaikan : Nilai R-squared yang disesuaikan menunjukkan kegunaan suatu model, disesuaikan berdasarkan jumlah prediktor dalam suatu model. Model dengan nilai Adjusted R-squared tertinggi dianggap yang terbaik.

2. AIC : Akaike Information Criterion (AIC) adalah metrik yang digunakan untuk membandingkan kesesuaian model regresi yang berbeda. Model dengan nilai AIC terendah dianggap terbaik.

Untungnya, kita dapat menghitung nilai R-squared dan AIC yang dipasang untuk model regresi di SAS menggunakan PROC REG dengan pernyataan SELECTION .

Kode berikut menunjukkan cara melakukan ini:

 /*perform stepwise multiple linear regression*/
proc reg data =my_data outest =est;
    model y=x1 x2 x3 x4 / selection=adjrsq aic ;
    output out =out p=pr=r;
run ;
quit ; 

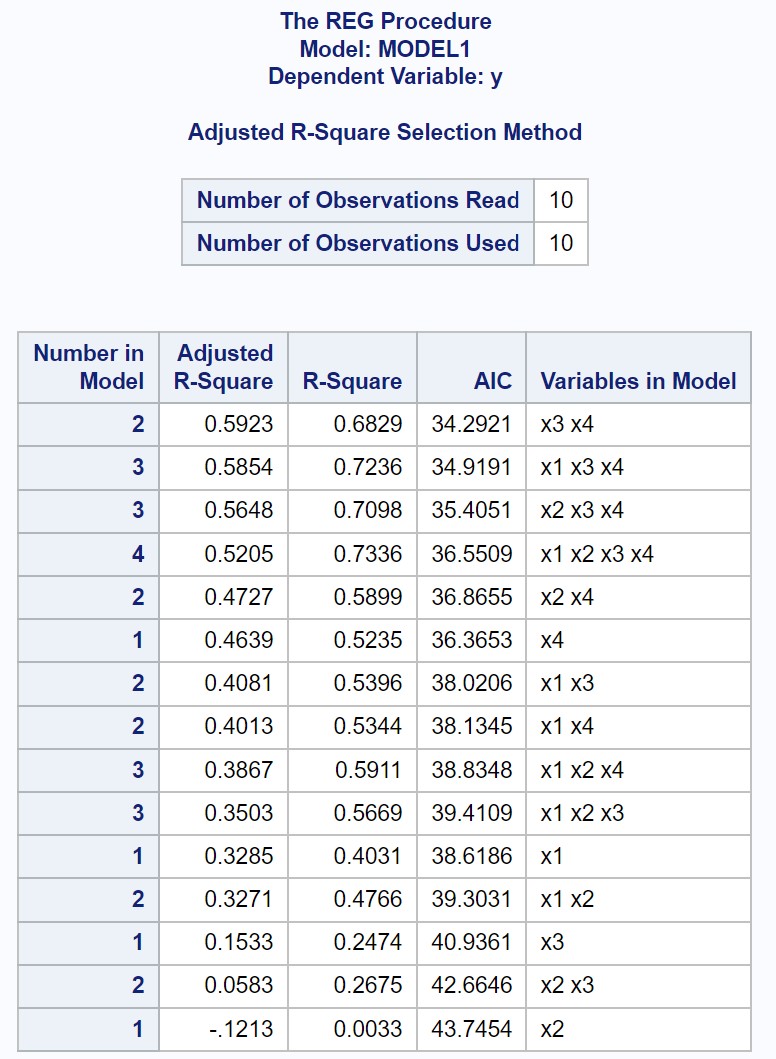
Outputnya menampilkan nilai R-squared dan AIC yang dipasang untuk setiap kemungkinan model regresi linier berganda.

Dari hasil tersebut terlihat bahwa nilai dengan nilai adjust R square tertinggi dan nilai AIC terendah merupakan model regresi yang hanya menggunakan x3 dan x4 sebagai variabel prediktor.

Dengan demikian, kami menyatakan bahwa model berikut adalah “yang terbaik” di antara semua model yang mungkin:

kamu = b ₀ + b ₁ (x3) + b ₂ (x4)

Model regresi khusus ini memiliki metrik berikut:

• Nilai R-kuadrat yang disesuaikan: 0,5923
• AIC: 34.2921

Catatan tentang pemilihan model regresi “terbaik”.

Perhatikan bahwa terkadang model dengan nilai R-kuadrat penyesuaian tertinggi tidak selalu juga memiliki nilai AIC terendah.

Saat memutuskan model regresi mana yang terbaik, R-squared dan AIC yang disesuaikan berfungsi sebagai saran, namun di dunia nyata Anda mungkin perlu menggunakan keahlian domain untuk menentukan model mana yang terbaik.

Mungkin juga bijaksana untuk memilih model yang pelit , yaitu model yang mencapai tingkat kesesuaian yang diinginkan dengan menggunakan variabel prediktor sesedikit mungkin.

Alasan di balik model jenis ini berasal dari gagasan pisau cukur Occam (kadang-kadang disebut “prinsip hemat”) yang mengatakan bahwa penjelasan paling sederhana mungkin adalah penjelasan yang benar.

Jika diterapkan pada statistik, model yang memiliki sedikit parameter tetapi mencapai tingkat kesesuaian yang memuaskan sebaiknya lebih dipilih daripada model yang memiliki banyak parameter dan hanya mencapai tingkat kesesuaian yang sedikit lebih tinggi.

Sumber daya tambahan

Tutorial berikut menjelaskan cara melakukan tugas umum lainnya di SAS:

Cara melakukan regresi linier sederhana di SAS
Cara melakukan regresi linier berganda di SAS
Cara melakukan regresi polinomial di SAS
Cara melakukan regresi logistik di SAS