Pengantar regresi lasso

Dalam regresi linier berganda biasa, kami menggunakan sekumpulan variabel prediktor p dan variabel respons agar sesuai dengan model dalam bentuk:

Y = β ₀ + β ₁ X _{1 +} β ₂ X ₂ + … + β _p

Emas:

• Y : Variabel respon
• X _j : variabel prediktif ^ke -j
• β _j : Efek rata-rata pada Y dari peningkatan satu unit X _j , dengan menganggap semua prediktor lainnya tetap
• ε : Istilah kesalahan

Nilai β ₀ , β ₁ , B ₂ , …, β _p dipilih menggunakan metode kuadrat terkecil , yang meminimalkan jumlah kuadrat residu (RSS):

RSS = Σ(y _saya – ŷ _saya ) ²

Emas:

• Σ : Simbol Yunani yang berarti jumlah
• y _i : nilai respon sebenarnya untuk observasi ^ke-i
• ŷ _i : Nilai respons yang diprediksi berdasarkan model regresi linier berganda

Namun, ketika variabel prediktor berkorelasi tinggi, multikolinearitas bisa menjadi masalah. Hal ini dapat membuat estimasi koefisien model tidak dapat diandalkan dan menunjukkan varians yang tinggi. Artinya, ketika model diterapkan pada kumpulan data baru yang belum pernah ada sebelumnya, kemungkinan besar kinerjanya akan buruk.

Salah satu cara untuk mengatasi masalah ini adalah dengan menggunakan metode yang dikenal sebagai regresi laso , yang berupaya meminimalkan hal-hal berikut:

RSS + λΣ|β _j |

dimana j beralih dari 1 ke p dan λ ≥ 0.

Suku kedua dalam persamaan ini dikenal sebagai penalti penarikan .

Ketika λ = 0, suku penalti ini tidak berpengaruh dan regresi laso menghasilkan perkiraan koefisien yang sama dengan kuadrat terkecil.

Namun, ketika λ mendekati tak terhingga, penalti penghapusan menjadi lebih berpengaruh dan variabel prediktif yang tidak dapat diimpor ke dalam model dikurangi menjadi nol dan bahkan ada yang dikeluarkan dari model.

Mengapa menggunakan regresi Lasso?

Keuntungan regresi laso dibandingkan regresi kuadrat terkecil adalah tradeoff bias-varians .

Ingatlah bahwa Mean Square Error (MSE) adalah metrik yang dapat kita gunakan untuk mengukur keakuratan model tertentu dan dihitung sebagai berikut:

MSE = Var( f̂( x ₀ )) + [Bias( f̂( x ₀ ))] ² + Var(ε)

MSE = Varians + Bias ² + Kesalahan yang tidak dapat direduksi

Ide dasar dari regresi laso adalah untuk memperkenalkan bias kecil sehingga varians dapat dikurangi secara signifikan, sehingga menghasilkan UMK yang lebih rendah secara keseluruhan.

Untuk mengilustrasikannya, perhatikan grafik berikut:

Perhatikan bahwa ketika λ meningkat, variansnya berkurang secara signifikan dengan peningkatan bias yang sangat kecil. Namun, setelah melewati titik tertentu, varians berkurang lebih lambat dan penurunan koefisien menyebabkan perkiraan yang terlalu rendah secara signifikan, yang menyebabkan peningkatan tajam dalam bias.

Kita dapat melihat dari grafik bahwa MSE pengujian paling rendah ketika kita memilih nilai λ yang menghasilkan trade-off optimal antara bias dan varians.

Ketika λ = 0, suku penalti dalam regresi laso tidak berpengaruh dan oleh karena itu menghasilkan estimasi koefisien yang sama dengan kuadrat terkecil. Namun, dengan meningkatkan λ hingga titik tertentu, kita dapat mengurangi MSE pengujian secara keseluruhan.

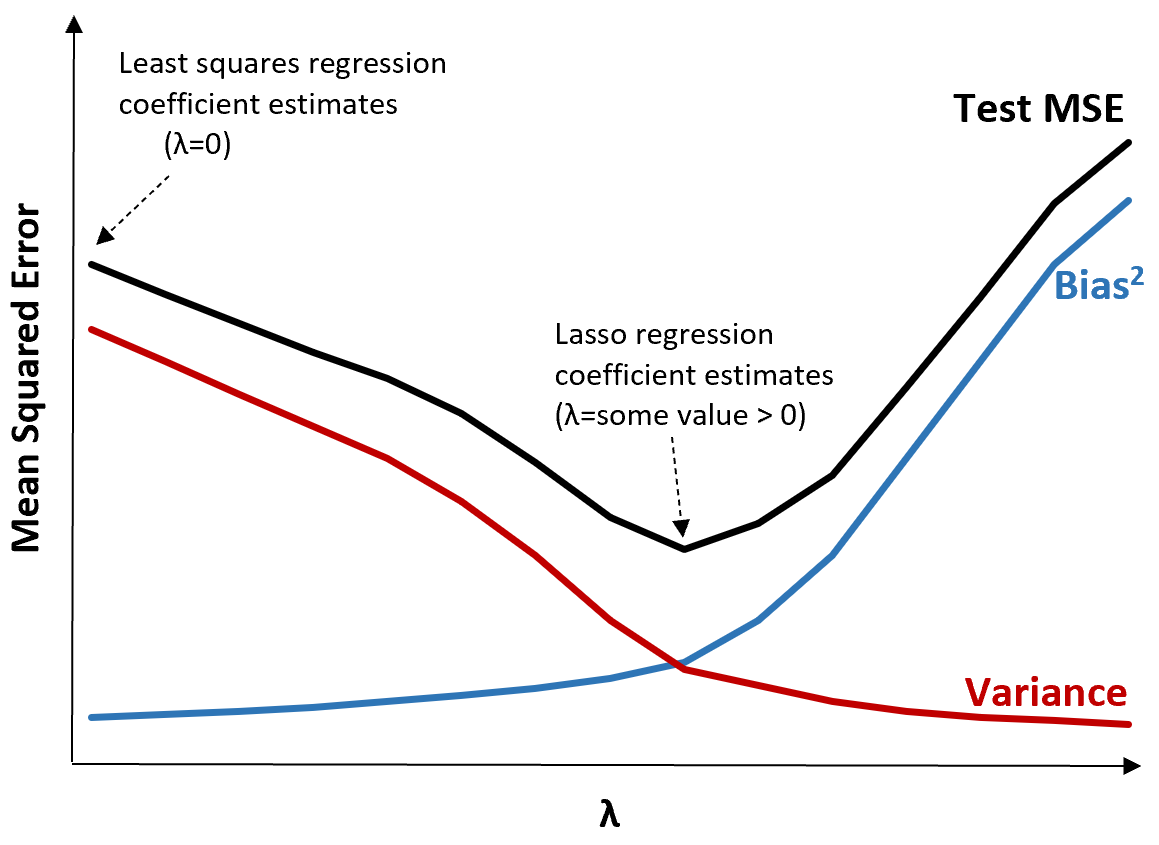
Artinya, fitting model dengan regresi laso akan menghasilkan error pengujian yang lebih kecil dibandingkan dengan fitting model dengan regresi kuadrat terkecil.

Regresi Lasso vs regresi Ridge

Regresi Lasso dan regresi Ridge keduanya dikenal sebagai metode regularisasi karena keduanya berupaya meminimalkan jumlah sisa kuadrat (RSS) serta jangka waktu penalti tertentu.

Dengan kata lain, mereka membatasi atau mengatur estimasi koefisien model.

Namun, ketentuan penalti yang mereka gunakan sedikit berbeda:

• Regresi Lasso berupaya meminimalkan RSS + λΣ|β _j |
• Regresi ridge berupaya meminimalkan RSS + λΣβ _j ²

Saat kita menggunakan regresi ridge, koefisien masing-masing prediktor dikurangi menjadi nol tetapi tidak ada satupun yang bisa mencapai nol sepenuhnya .

Sebaliknya, jika kita menggunakan regresi laso, ada kemungkinan beberapa koefisien menjadi nol sepenuhnya ketika λ menjadi cukup besar.

Secara teknis, regresi laso mampu menghasilkan model “sparse”, yaitu model yang hanya menyertakan sebagian variabel prediktor.

Hal ini menimbulkan pertanyaan: apakah regresi ridge atau regresi laso lebih baik?

Jawabannya: tergantung!

Dalam kasus di mana hanya sejumlah kecil variabel prediktor yang signifikan, regresi laso cenderung bekerja lebih baik karena mampu mereduksi sepenuhnya variabel-variabel yang tidak signifikan menjadi nol dan menghapusnya dari model.

Namun, ketika banyak variabel prediktor signifikan dalam model dan koefisiennya kira-kira sama, regresi ridge cenderung bekerja lebih baik karena semua prediktor tetap berada dalam model.

Untuk menentukan model mana yang paling efektif dalam membuat prediksi, kami melakukan validasi silang k-fold . Model mana pun yang menghasilkan mean square error (MSE) terendah adalah model terbaik untuk digunakan.

Langkah-langkah melakukan regresi laso dalam praktiknya

Langkah-langkah berikut dapat digunakan untuk melakukan regresi laso:

Langkah 1: Hitung matriks korelasi dan nilai VIF untuk variabel prediktor.

Pertama, kita perlu membuat matriks korelasi dan menghitung nilai VIF (variance inflasi faktor) untuk setiap variabel prediktor.

Jika kita mendeteksi korelasi yang kuat antara variabel prediktor dan nilai VIF yang tinggi (beberapa teks mendefinisikan nilai VIF “tinggi” sebagai 5 sementara yang lain menggunakan 10), maka regresi laso mungkin tepat.

Namun, jika tidak terdapat multikolinearitas pada data, mungkin tidak perlu dilakukan regresi laso terlebih dahulu. Sebagai gantinya, kita dapat melakukan regresi kuadrat terkecil biasa.

Langkah 2: Sesuaikan model regresi laso dan pilih nilai λ.

Setelah kami menentukan bahwa regresi laso sesuai, kami dapat menyesuaikan modelnya (menggunakan bahasa pemrograman populer seperti R atau Python) menggunakan nilai optimal untuk λ.

Untuk menentukan nilai λ yang optimal, kita dapat menyesuaikan beberapa model menggunakan nilai λ yang berbeda dan memilih λ sebagai nilai yang menghasilkan pengujian MSE terendah.

Langkah 3: Bandingkan regresi laso dengan regresi ridge dan regresi kuadrat terkecil biasa.

Terakhir, kita dapat membandingkan model regresi laso dengan model regresi ridge dan model regresi kuadrat terkecil untuk menentukan model mana yang menghasilkan uji MSE terendah menggunakan validasi silang k-fold.

Bergantung pada hubungan antara variabel prediktor dan variabel respons, sangat mungkin bahwa salah satu dari ketiga model ini akan mengungguli model lainnya dalam skenario yang berbeda.

Regresi Lasso dalam R & Python

Tutorial berikut menjelaskan cara melakukan regresi laso di R dan Python:

Regresi Lasso di R (langkah demi langkah)
Regresi Lasso dengan Python (Langkah demi Langkah)