Pengantar regresi linier sederhana

Regresi linier sederhana merupakan salah satu metode statistik yang dapat Anda gunakan untuk memahami hubungan antara dua variabel, x dan y.

Variabel, x , dikenal sebagai variabel prediktor .

Variabel lainnya, y , dikenal sebagai variabel respon .

Misalnya, kita memiliki kumpulan data berikut dengan berat dan tinggi badan tujuh orang:

Biarkan berat badan menjadi variabel prediktor dan biarkan tinggi badan menjadi variabel respon.

Jika kita membuat grafik kedua variabel ini menggunakan scatterplot, dengan bobot pada sumbu x dan tinggi pada sumbu y, maka akan terlihat seperti ini:

Misalkan kita ingin memahami hubungan antara berat badan dan tinggi badan. Dari diagram sebar kita dapat melihat dengan jelas bahwa seiring bertambahnya berat badan, tinggi badan juga cenderung meningkat, tetapi untuk benar-benar mengukur hubungan antara berat badan dan tinggi badan ini kita perlu menggunakan regresi linier.

Dengan menggunakan regresi linier, kita dapat menemukan garis yang paling “sesuai” dengan data kita. Garis ini dikenal sebagai garis regresi kuadrat terkecil dan dapat digunakan untuk membantu kita memahami hubungan antara berat badan dan tinggi badan.

Biasanya, Anda akan menggunakan perangkat lunak seperti Microsoft Excel, SPSS, atau kalkulator grafik untuk mencari persamaan garis ini.

Rumus garis yang paling sesuai ditulis:

ŷ = b ₀ + b ₁ x

dimana ŷ adalah nilai prediksi variabel respon, b ₀ adalah intersep, b ₁ adalah koefisien regresi, dan x adalah nilai variabel prediktor.

Terkait: 4 Contoh Penggunaan Regresi Linier dalam Kehidupan Nyata

Temukan “jalur yang paling cocok”

Untuk contoh ini, kita cukup memasukkan data kita ke dalam kalkulator regresi linier statistik dan tekan Hitung :

Kalkulator secara otomatis menemukan garis regresi kuadrat terkecil :

ŷ = 32,7830 + 0,2001x

Jika kita memperkecil tampilan diagram sebar sebelumnya dan menambahkan garis ini ke grafik, tampilannya akan seperti ini:

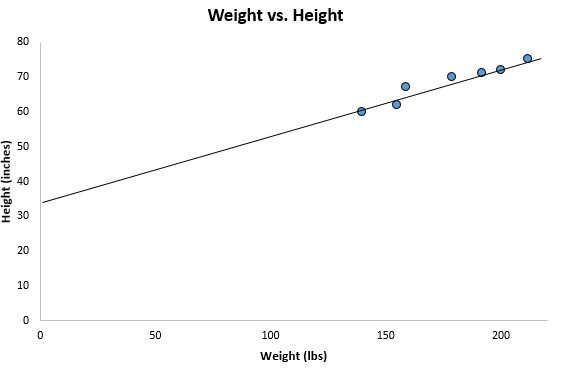
Perhatikan bagaimana titik data kita tersebar di sekitar garis ini. Memang benar, garis regresi kuadrat terkecil ini adalah garis yang paling sesuai dengan data kita di antara semua kemungkinan garis yang dapat kita gambar.

Bagaimana menafsirkan garis regresi kuadrat terkecil

Berikut cara mengartikan garis regresi kuadrat terkecil ini: ŷ = 32,7830 + 0,2001x

_b0 = 32,7830 . Artinya ketika variabel prediktor berat badan adalah nol pon, maka tinggi badan yang diprediksi adalah 32,7830 inci. Terkadang nilai b ₀ berguna untuk diketahui, tetapi dalam contoh spesifik ini tidak masuk akal untuk menafsirkan b ₀ karena seseorang tidak dapat memiliki berat nol pon.

_b1 = 0,2001 . Artinya kenaikan satu satuan pada x dikaitkan dengan kenaikan 0,2001 satuan pada y . Dalam hal ini, peningkatan berat badan sebesar satu pon dikaitkan dengan peningkatan tinggi badan sebesar 0,2001 inci.

Cara menggunakan garis regresi kuadrat terkecil

Dengan menggunakan garis regresi kuadrat terkecil ini, kita dapat menjawab pertanyaan seperti:

Untuk seseorang yang beratnya 170 pon, berapa tinggi badan yang kita harapkan?

Untuk menjawab pertanyaan ini, kita cukup memasukkan 170 ke dalam garis regresi untuk x dan menyelesaikan untuk y:

ŷ = 32,7830 + 0,2001(170) = 66,8 inci

Untuk seseorang yang beratnya 150 pon, berapa tinggi badan yang kita harapkan?

Untuk menjawab pertanyaan ini, kita dapat memasukkan 150 ke dalam garis regresi untuk x dan menyelesaikan untuk y:

ŷ = 32,7830 + 0,2001(150) = 62,798 inci

Perhatian: Saat menggunakan persamaan regresi untuk menjawab pertanyaan seperti ini, pastikan untuk hanya menggunakan nilai variabel prediktor yang berada dalam rentang variabel prediktor dalam kumpulan data. asal yang kami gunakan untuk menghasilkan garis regresi kuadrat terkecil. Misalnya, bobot dalam kumpulan data kami berkisar antara 140 dan 212 pon. Jadi masuk akal untuk menjawab pertanyaan tentang tinggi badan yang diharapkan ketika berat badan antara 140 dan 212 pon.

Koefisien determinasi

Salah satu cara untuk mengukur seberapa cocok garis regresi kuadrat terkecil dengan data adalah dengan menggunakan koefisien determinasi yang dilambangkan dengan R ² .

Koefisien determinasi merupakan proporsi variansi variabel respon yang dapat dijelaskan oleh variabel prediktor.

Koefisien determinasi dapat bervariasi dari 0 hingga 1. Nilai 0 menunjukkan bahwa variabel respon tidak dapat dijelaskan sama sekali oleh variabel prediktor. Nilai 1 menunjukkan bahwa variabel respon dapat dijelaskan dengan sempurna tanpa kesalahan oleh variabel prediktor.

R2 ^antara 0 dan 1 menunjukkan sejauh mana variabel respon dapat dijelaskan oleh variabel prediktor. Misalnya, R ² sebesar 0,2 menunjukkan bahwa 20% varians dalam variabel respon dapat dijelaskan oleh variabel prediktor; R ² sebesar 0,77 menunjukkan bahwa 77% varians variabel respon dapat dijelaskan oleh variabel prediktor.

Perhatikan bahwa pada hasil sebelumnya kami memperoleh R ² sebesar 0,9311, yang menunjukkan bahwa 93,11% variabilitas tinggi badan dapat dijelaskan oleh variabel prediktor berat badan:

Ini memberi tahu kita bahwa berat badan adalah indikator tinggi badan yang sangat baik.

Asumsi Regresi Linier

Agar hasil model regresi linier valid dan dapat diandalkan, kita harus memverifikasi bahwa empat asumsi berikut terpenuhi:

1. Hubungan linier : Terdapat hubungan linier antara variabel bebas, x, dan variabel terikat, y.

2. Independensi: Residunya bersifat independen. Secara khusus, tidak ada korelasi antara residu yang berurutan dalam data deret waktu.

3. Homoskedastisitas : Residual mempunyai varian yang konstan pada setiap level x.

4. Normalitas: Residual model berdistribusi normal.

Jika satu atau lebih asumsi ini tidak terpenuhi, maka hasil regresi linier kami mungkin tidak dapat diandalkan atau bahkan menyesatkan.

Lihat artikel ini untuk penjelasan masing-masing asumsi, cara menentukan apakah asumsi tersebut terpenuhi, dan apa yang harus dilakukan jika asumsi tersebut tidak terpenuhi.