Regresi linier berganda dengan tangan (langkah demi langkah)
Regresi linier berganda merupakan metode yang dapat kita gunakan untuk mengukur hubungan antara dua atau lebih variabel prediktor dan variabel respon .
Tutorial ini menjelaskan cara melakukan regresi linier berganda secara manual.
Contoh: regresi linier berganda dengan tangan
Misalkan kita mempunyai kumpulan data berikut dengan variabel respon y dan dua variabel prediktor x 1 dan x 2 :
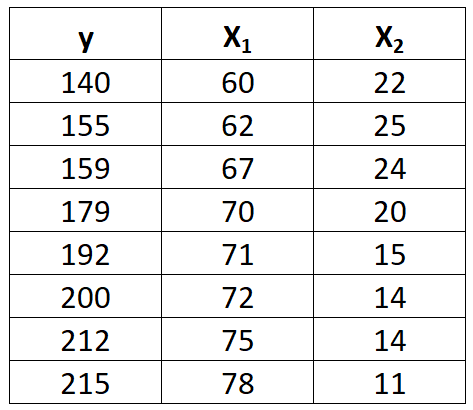
Selesaikan langkah-langkah berikut untuk menyesuaikan model regresi linier berganda dengan kumpulan data ini.
Langkah 1: Hitung x 1 2 , x 2 2 , x 1 y, x 2 y dan x 1 x 2 .
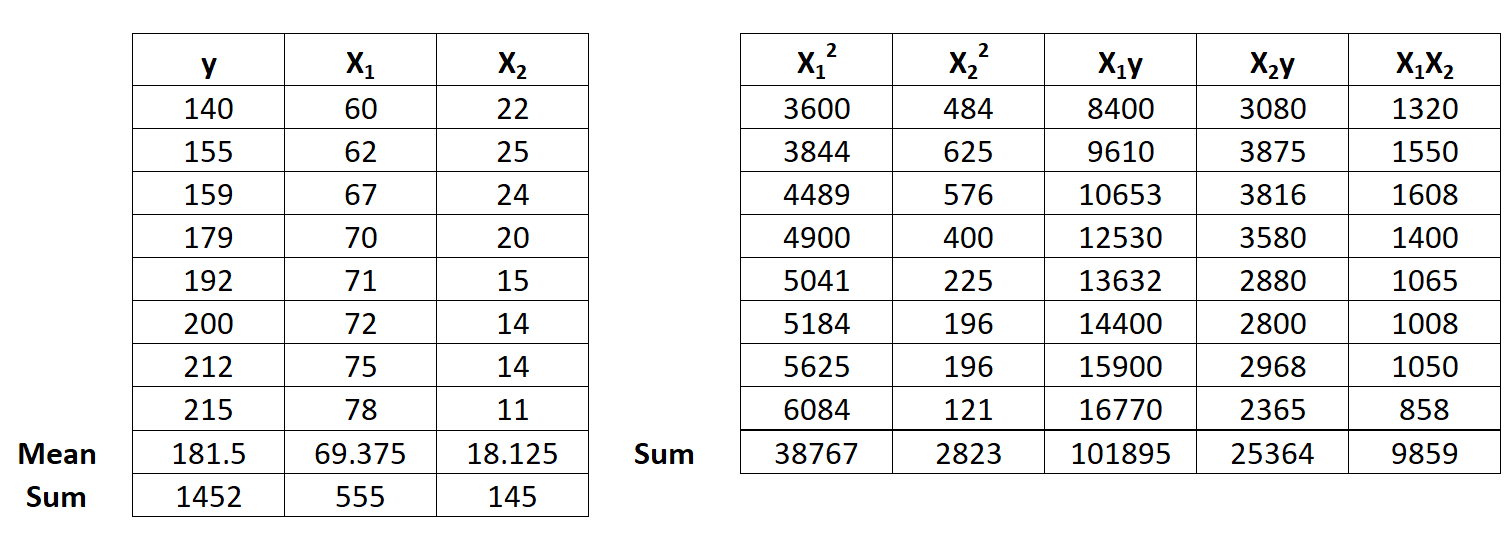
Langkah 2: Hitung jumlah regresi.
Selanjutnya, lakukan perhitungan jumlah regresi berikut:
- Σx12 = ΣX12 – ( ΣX1 ) 2 / n = 38,767 – (555) 2 / 8 = 263,875
- Σx22 = ΣX22 – ( ΣX2 ) 2 / n = 2823 – (145) 2 / 8 = 194,875
- Σ x 1 kamu = Σ
- Σ x 2 kamu = Σ
- Σ x 1 x 2 = Σ
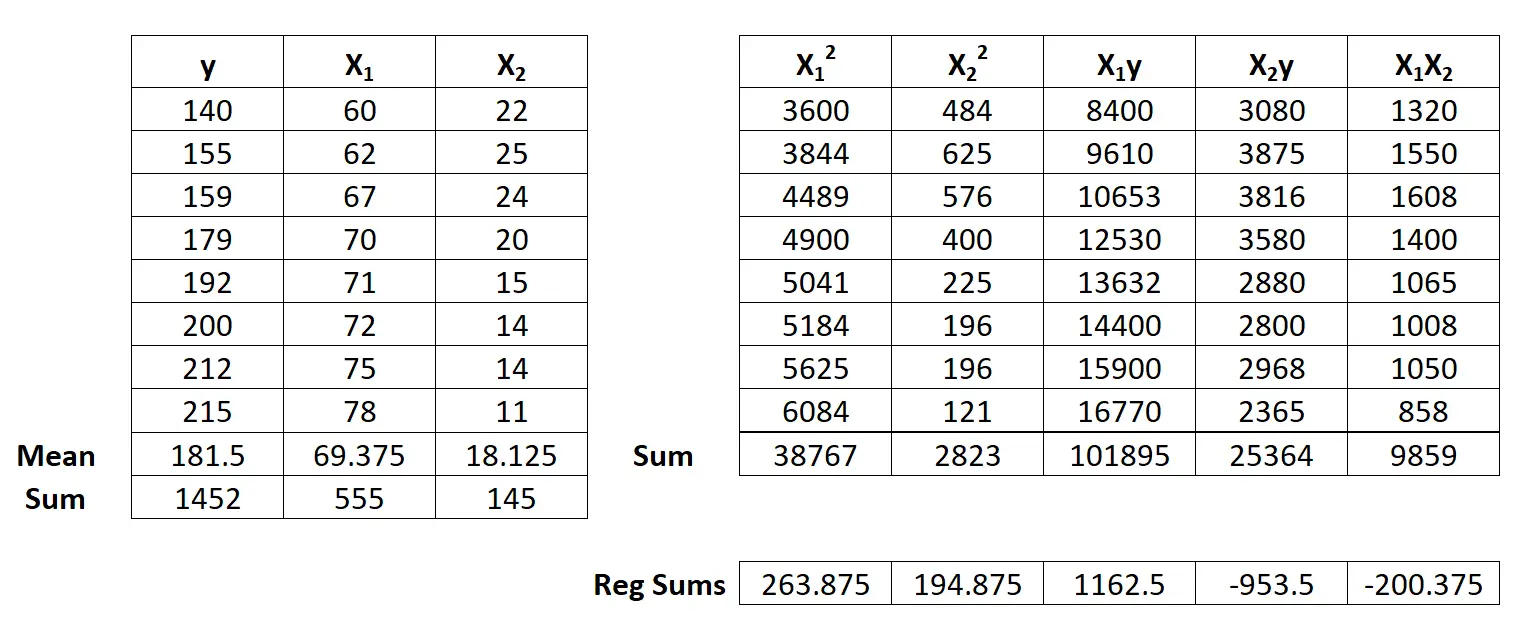
Langkah 3: Hitung b 0 , b 1 dan b 2 .
Rumus untuk menghitung b 1 adalah: [(Σx 2 2 )(Σx 1 y) – (Σx 1 x 2 )(Σx 2 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
Jadi, b 1 = [(194.875)(1162.5) – (-200.375)(-953.5)] / [(263.875) (194.875) – (-200.375) 2 ] = 3.148
Rumus untuk menghitung b 2 adalah: [(Σx 1 2 )(Σx 2 y) – (Σx 1 x 2 )(Σx 1 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
Jadi, b 2 = [(263.875)(-953.5) – (-200.375)(1152.5)] / [(263.875) (194.875) – (-200.375) 2 ] = -1.656
Rumus untuk menghitung b 0 adalah: y – b 1 X 1 – b 2 X 2
Jadi, b 0 = 181,5 – 3,148(69,375) – (-1,656)(18,125) = -6,867
Langkah 5: Tempatkan b 0 , b 1 dan b 2 ke dalam estimasi persamaan regresi linier.
Persamaan regresi linier yang diestimasi adalah: ŷ = b 0 + b 1 *x 1 + b 2 *x 2
Dalam contoh kita, ŷ = -6,867 + 3,148x 1 – 1,656x 2
Bagaimana menafsirkan persamaan regresi linier berganda
Berikut cara menafsirkan persamaan regresi linier taksiran ini: ŷ = -6,867 + 3,148x 1 – 1,656x 2
b0 = -6.867 . Ketika kedua variabel prediktor sama dengan nol, maka nilai rata-rata y sebesar -6,867.
b1 = 3,148 . Peningkatan satu unit pada x 1 dikaitkan dengan peningkatan rata-rata 3,148 unit pada y, dengan asumsi x 2 tetap konstan.
b2 = -1,656 . Peningkatan satu unit pada x 2 dikaitkan dengan penurunan rata-rata 1.656 unit pada y, dengan asumsi x 1 tetap konstan.
Sumber daya tambahan
Pengantar Regresi Linier Berganda
Cara melakukan regresi linier sederhana dengan tangan
Tentang Penulis
Benjamin anderson
Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya