Cara melakukan regresi linier berganda di sas

Regresi linier berganda merupakan salah satu metode yang dapat kita gunakan untuk memahami hubungan antara dua atau lebih variabel prediktor dan suatu variabel respon .

Tutorial ini menjelaskan cara melakukan regresi linier berganda di SAS.

Langkah 1: Buat datanya

Misalkan kita ingin menyesuaikan model regresi linier berganda yang menggunakan jumlah jam yang dihabiskan untuk belajar dan jumlah ujian praktik yang diambil untuk memprediksi nilai ujian akhir siswa:

Nilai ujian = β ₀ + β ₁ (jam) + β ₂ (persiapan ujian)

Pertama, kita akan menggunakan kode berikut untuk membuat kumpulan data yang berisi informasi ini untuk 20 siswa:

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 96
5 4 90
3 4 82
4 4 85
6 5 99
2 1 83
1 0 62
2 1 76
;
run ;

Langkah 2: Lakukan Regresi Linier Berganda

Selanjutnya, kita akan menggunakan proc reg untuk menyesuaikan model regresi linier berganda dengan data:

 /*fit multiple linear regression model*/
proc reg data =exam_data;
    model score = hours prep_exams;
run ; 

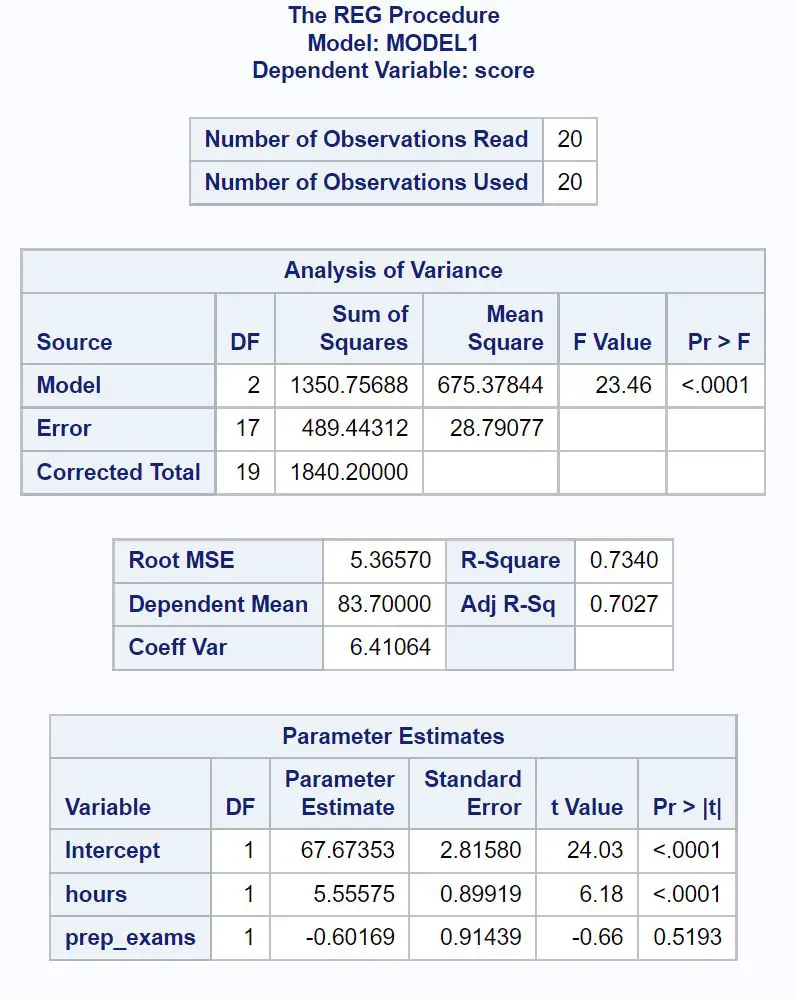
Berikut cara menafsirkan angka paling relevan di setiap tabel:

Tabel analisis kesenjangan:

Nilai F keseluruhan model regresi adalah 23,46 dan nilai p yang sesuai adalah <0,0001 .

Karena nilai p ini kurang dari 0,05, kami menyimpulkan bahwa model regresi secara keseluruhan signifikan secara statistik.

Tabel kesesuaian model:

Nilai R-Square menunjukkan persentase variasi nilai ujian yang dapat dijelaskan oleh jumlah jam belajar dan jumlah persiapan ujian yang diambil.

Secara umum, semakin besar nilai R-squared suatu model regresi maka semakin baik pula variabel prediktor dalam memprediksi nilai variabel respon.

Dalam hal ini, 73,4% variasi nilai ujian dapat dijelaskan oleh jumlah jam belajar dan jumlah persiapan ujian yang diambil.

Nilai Root MSE juga berguna untuk diketahui. Ini mewakili jarak rata-rata antara nilai yang diamati dan garis regresi.

Dalam model regresi ini, nilai yang diamati rata-rata menyimpang sebesar 5,3657 satuan dari garis regresi.

Tabel estimasi parameter:

Kita dapat menggunakan nilai estimasi parameter dalam tabel ini untuk menulis persamaan regresi yang sesuai:

Skor ujian = 67.674 + 5.556*(jam) – 0.602*(ujian_persiapan)

Kita dapat menggunakan persamaan ini untuk mengetahui perkiraan nilai ujian siswa, berdasarkan jumlah jam belajar dan jumlah ujian praktik yang telah mereka ikuti.

Misalnya, seorang siswa yang belajar selama 3 jam dan mengikuti 2 ujian persiapan harus mendapat nilai ujian 83,1 :

Perkiraan nilai ujian = 67.674 + 5.556*(3) – 0.602*(2) = 83.1

Nilai p untuk jam (<0,0001) kurang dari 0,05, yang berarti memiliki hubungan yang signifikan secara statistik dengan hasil ujian.

Namun, nilai p untuk ujian persiapan (0,5193) tidak kurang dari 0,05, yang berarti tidak memiliki hubungan yang signifikan secara statistik dengan hasil ujian.

Kami mungkin memutuskan untuk menghapus ujian persiapan dari model, karena ujian tersebut tidak signifikan secara statistik, dan sebagai gantinya melakukanregresi linier sederhana menggunakan jam belajar sebagai satu-satunya variabel prediktor.

Sumber daya tambahan

Tutorial berikut menjelaskan cara melakukan tugas umum lainnya di SAS:

Cara menghitung korelasi di SAS
Cara melakukan regresi linier sederhana di SAS
Cara melakukan ANOVA satu arah di SAS