Regresi linier sederhana

Oleh Benjamin anderson Agustus 2, 2023 Statistik 0 Komentar

Artikel ini menjelaskan apa itu regresi linier sederhana dalam statistik dan bagaimana cara kerjanya. Demikian pula, Anda akan menemukan latihan regresi linier sederhana yang diselesaikan dan, sebagai tambahan, kalkulator regresi linier sederhana online.

Apa itu regresi linier sederhana?

Regresi linier sederhana adalah model statistik yang digunakan untuk menghubungkan suatu variabel independen dan kami mencoba memperkirakan hubungan yang ada antara kedua variabel tersebut.

Oleh karena itu, regresi linier sederhana digunakan untuk mencari persamaan yang menghubungkan dua variabel secara linier. Logikanya, hubungan kedua variabel harus linier, jika tidak maka harus digunakan model regresi jenis lain.

Persamaan model regresi linier sederhana terdiri dari dua koefisien: konstanta persamaan (b ₀ ) dan koefisien korelasi kedua variabel (b ₁ ). Oleh karena itu, persamaan model regresi linier sederhana adalah y=b ₀ +b ₁ x.

$y=b_0+b_1x$

Persamaan regresi linier sederhana digambarkan sebagai garis lurus, sehingga koefisien b ₀ adalah titik potong dan koefisien b ₁ adalah kemiringan garis.

Rumus regresi linier sederhana

Rumus untuk menghitung koefisien regresi linier sederhana adalah sebagai berikut:

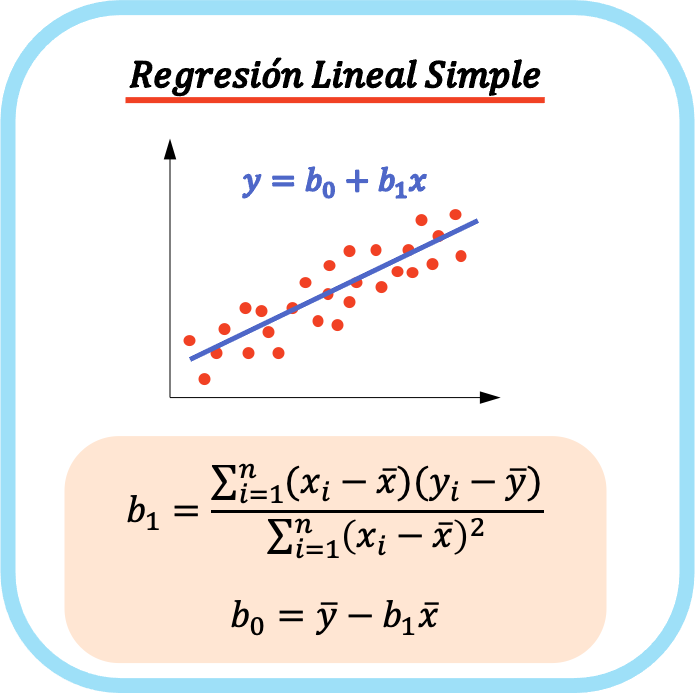
👉 Anda dapat menggunakan kalkulator di bawah ini untuk menghitung koefisien regresi linier sederhana untuk kumpulan data apa pun.

Tentunya persamaan yang dihasilkan dari model regresi linier sederhana tidak akan dapat menebak nilai pasti dari seluruh observasi, karena model ini hanya berusaha mencari persamaan yang mendekati hubungan kedua variabel. Dengan demikian, residu didefinisikan sebagai selisih antara nilai sebenarnya dan nilai yang diperkirakan oleh model regresi linier.

$e_i=y_i-\widehat{y}_i$

Perhatikan bahwa tujuan model regresi linier sederhana adalah untuk meminimalkan kuadrat dari residu, yaitu regresi linier sederhana didasarkan pada kriteria kuadrat terkecil .

Contoh konkrit regresi linier sederhana

Untuk menyelesaikan pemahaman metode regresi linier sederhana, berikut adalah contoh praktis langkah demi langkah di mana persamaan model regresi linier sederhana dihitung dari sekumpulan data statistik.

Setelah mengikuti ujian statistik, lima siswa ditanyai berapa jam belajar yang telah mereka curahkan untuk ujian tersebut. Datanya disajikan pada tabel di bawah ini. Lakukan model regresi linier sederhana dari data statistik yang dikumpulkan untuk menghubungkan jam belajar secara linier dengan nilai yang dicapai.

Untuk menjalankan model regresi linier sederhana kita harus menentukan koefisien b ₀ dan b ₁ dari persamaan tersebut dan, untuk ini, kita harus menggunakan rumus yang terlihat pada bagian di atas.

Namun untuk menerapkan rumus regresi linier sederhana, pertama-tama kita harus menghitung mean variabel independen dan mean variabel dependen:

$\begin{array}{c}\overline{x}=\cfrac{11+5+10+12+7}{5}=9\\[4ex]\overline{y}=\cfrac{7+4+5+8+6}{5}=6\end{array}$

Sekarang setelah kita mengetahui rata-rata variabel, kita menghitung koefisien b ₁ model menggunakan rumus yang sesuai:

$\begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[10ex] b_1=\cfrac{\begin{array}{c}(11-9)(7-6)+(5-9)(4-6)+(10-9)(5-6)+\\+(12-9)(8-6)+(7-9)(6-6)\end{array}}{(11-9)^2+(5-9)^2+(10-9)^2+(12-9)^2+(7-9)^2}\\[6ex]b_1=0,4412\end{array}$

Terakhir, kami menghitung koefisien b ₀ model menggunakan rumus yang sesuai:

$\begin{array}{l}b_0=\overline{y}-b_1\overline{x}\\[3ex]b_0=6-0,4412\cdot 9 \\[3ex]b_0=2,0294\end{array}$

Singkatnya, persamaan model regresi linier sederhana dari permasalahan tersebut adalah:

$y=2,0294+0,4412x$

Di bawah ini Anda dapat melihat representasi grafis dari data sampel serta garis lurus model regresi linier sederhana:

Terakhir, setelah kita menghitung persamaan model regresi linier sederhana, yang tersisa hanyalah menginterpretasikan hasil yang diperoleh. Untuk itu, penting untuk menghitung koefisien determinasi model regresi, Anda dapat melihat cara melakukannya dengan mencari artikel terkait di situs web kami.

Asumsi Regresi Linier Sederhana

Untuk melakukan regresi linier sederhana, asumsi berikut harus dipenuhi:

Kemandirian : residu yang diamati harus independen satu sama lain. Cara umum untuk memastikan independensi model adalah dengan menambahkan keacakan pada proses pengambilan sampel.
Homoskedastisitas : Harus ada homogenitas varians dari residu, yaitu variabilitas dari residu harus konstan.
Normalitas : Residunya harus berdistribusi normal, atau dengan kata lain harus mengikuti distribusi normal dengan mean 0.
Linearitas – Hubungan antara variabel independen dan variabel dependen harus linier.

Kalkulator Regresi Linier Sederhana

Masukkan contoh data ke dalam kalkulator di bawah ini agar sesuai dengan model regresi linier sederhana antara dua variabel. Anda perlu memisahkan pasangan datanya, sehingga pada kotak pertama hanya terdapat nilai variabel bebas X dan pada kotak kedua hanya terdapat nilai variabel terikat Y.

Data harus dipisahkan dengan spasi dan dimasukkan menggunakan titik sebagai pemisah desimal.

Regresi linier sederhana dan berganda

Terakhir, kita akan melihat apa perbedaan antara regresi linier sederhana dan regresi linier berganda, karena keduanya merupakan dua jenis regresi linier yang sering digunakan dalam statistik.

Regresi linier berganda memungkinkan untuk menghubungkan secara matematis dua atau lebih variabel penjelas ke variabel respon. Artinya, dalam regresi linier berganda, dibuat model yang paling sedikit terdapat dua variabel bebas.

Oleh karena itu, perbedaan antara regresi linier sederhana dan regresi linier berganda terletak pada jumlah variabel bebasnya. Pada regresi linier sederhana hanya terdapat satu variabel bebas, sedangkan pada regresi linier berganda terdapat dua atau lebih variabel bebas.

➤ Lihat: Regresi linier berganda

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya