Cara melakukan regresi linier sederhana di sas

Regresi linier sederhana merupakan teknik yang dapat kita gunakan untuk memahami hubungan antara variabel prediktor dan variabel respon .

Teknik ini menemukan garis yang paling “sesuai” dengan data dan mengambil bentuk berikut:

ŷ = b ₀ + b ₁ x

Emas:

• ŷ : Perkiraan nilai respons
• b ₀ : Asal garis regresi
• b ₁ : Kemiringan garis regresi

Persamaan ini membantu kita memahami hubungan antara variabel prediktor dan variabel respon.

Contoh langkah demi langkah berikut menunjukkan cara melakukan regresi linier sederhana di SAS.

Langkah 1: Buat datanya

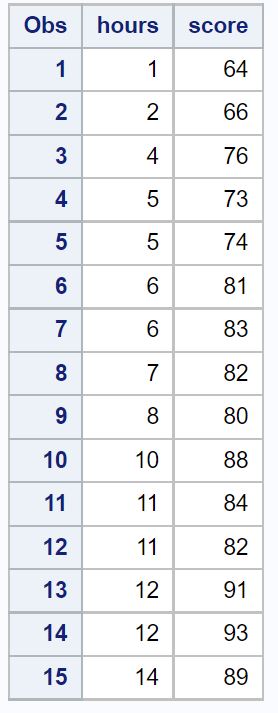
Untuk contoh ini, kita akan membuat dataset yang berisi jumlah jam belajar dan nilai ujian akhir 15 siswa.

Kami akan menyesuaikan model regresi linier sederhana dengan menggunakan jam sebagai variabel prediktor dan skor sebagai variabel respon.

Kode berikut menunjukkan cara membuat kumpulan data ini di SAS:

 /*create dataset*/
data exam_data;
    input hours score;
    datalines ;
1 64
2 66
4 76
5 73
5 74
6 81
6 83
7 82
8 80
10 88
11 84
11 82
12 91
12 93
14 89
;
run ;

/*view dataset*/
proc print data =exam_data;

Langkah 2: Sesuaikan model regresi linier sederhana

Selanjutnya, kita akan menggunakan proc reg agar sesuai dengan model regresi linier sederhana:

 /*fit simple linear regression model*/
proc reg data =exam_data;
   model score = hours;
run ; 

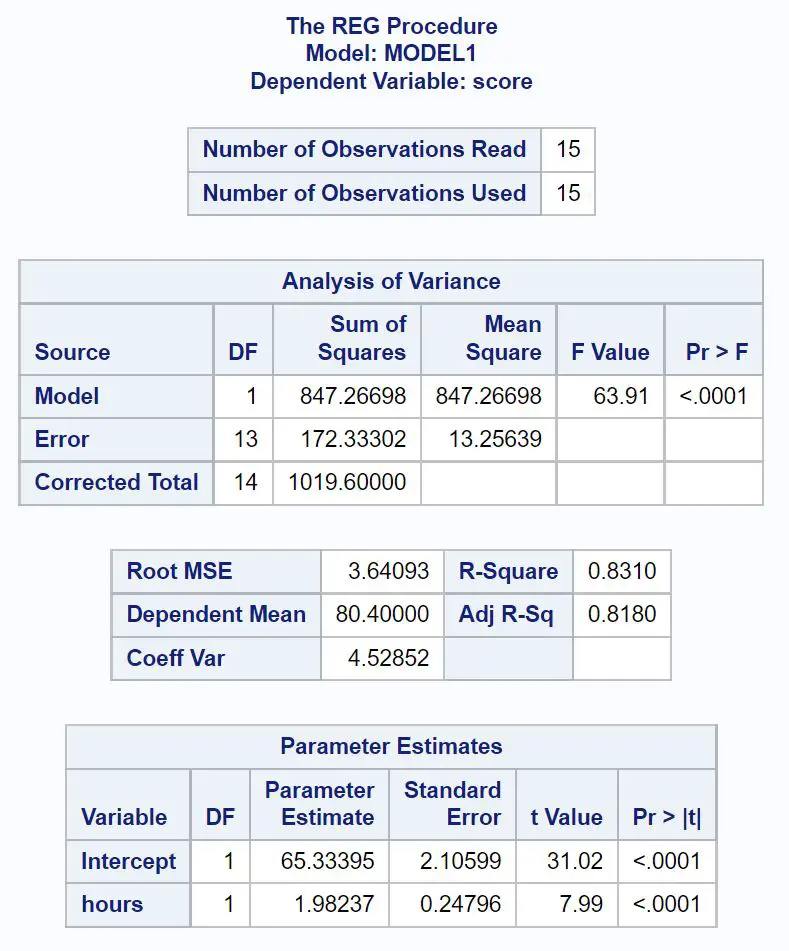
Berikut cara menginterpretasikan nilai terpenting dari setiap tabel pada hasil:

Tabel analisis kesenjangan:

Nilai F keseluruhan model regresi adalah 63,91 dan nilai p yang sesuai adalah <0,0001 .

Karena nilai p ini kurang dari 0,05, kami menyimpulkan bahwa model regresi secara keseluruhan signifikan secara statistik. Dengan kata lain, jam kerja adalah variabel yang berguna untuk memprediksi hasil ujian.

Tabel kesesuaian model:

Nilai R-Square menunjukkan persentase variasi nilai ujian yang dapat dijelaskan oleh jumlah jam belajar.

Secara umum, semakin besar nilai R-squared suatu model regresi maka semakin baik pula variabel prediktor dalam memprediksi nilai variabel respon.

Dalam hal ini, 83,1% variasi nilai ujian dapat dijelaskan oleh jumlah jam belajar. Nilai ini cukup tinggi, menunjukkan bahwa jam belajar merupakan variabel yang sangat berguna dalam memprediksi hasil ujian.

Tabel estimasi parameter:

Dari tabel ini kita dapat melihat persamaan regresi yang sesuai:

Skor = 65,33 + 1,98*(jam)

Kami menafsirkan hal ini berarti bahwa setiap jam belajar tambahan dikaitkan dengan peningkatan rata-rata skor ujian sebesar 1,98 poin .

Nilai aslinya memberitahu kita bahwa rata-rata nilai ujian untuk siswa yang belajar selama nol jam adalah 65,33 .

Kita juga dapat menggunakan persamaan ini untuk mencari nilai ujian yang diharapkan berdasarkan jumlah jam belajar seorang siswa.

Misalnya, seorang siswa yang belajar selama 10 jam harus mencapai nilai ujian 85,13 :

Skor = 65,33 + 1,98*(10) = 85,13

Karena nilai p (<0,0001) untuk jam kerja kurang dari 0,05 pada tabel ini, kami menyimpulkan bahwa ini adalah variabel prediktor yang signifikan secara statistik.

Langkah 3: Analisis plot sisa

Regresi linier sederhana membuat dua asumsi penting tentang residu model :

• Residunya berdistribusi normal.
• Residual tersebut mempunyai varians yang sama (“ homoskedastisitas ”) pada setiap level variabel prediktor.

Jika asumsi ini tidak dipenuhi, maka hasil model regresi kami mungkin tidak dapat diandalkan.

Untuk memverifikasi bahwa asumsi ini terpenuhi, kita dapat menganalisis plot sisa yang ditampilkan SAS secara otomatis di output:

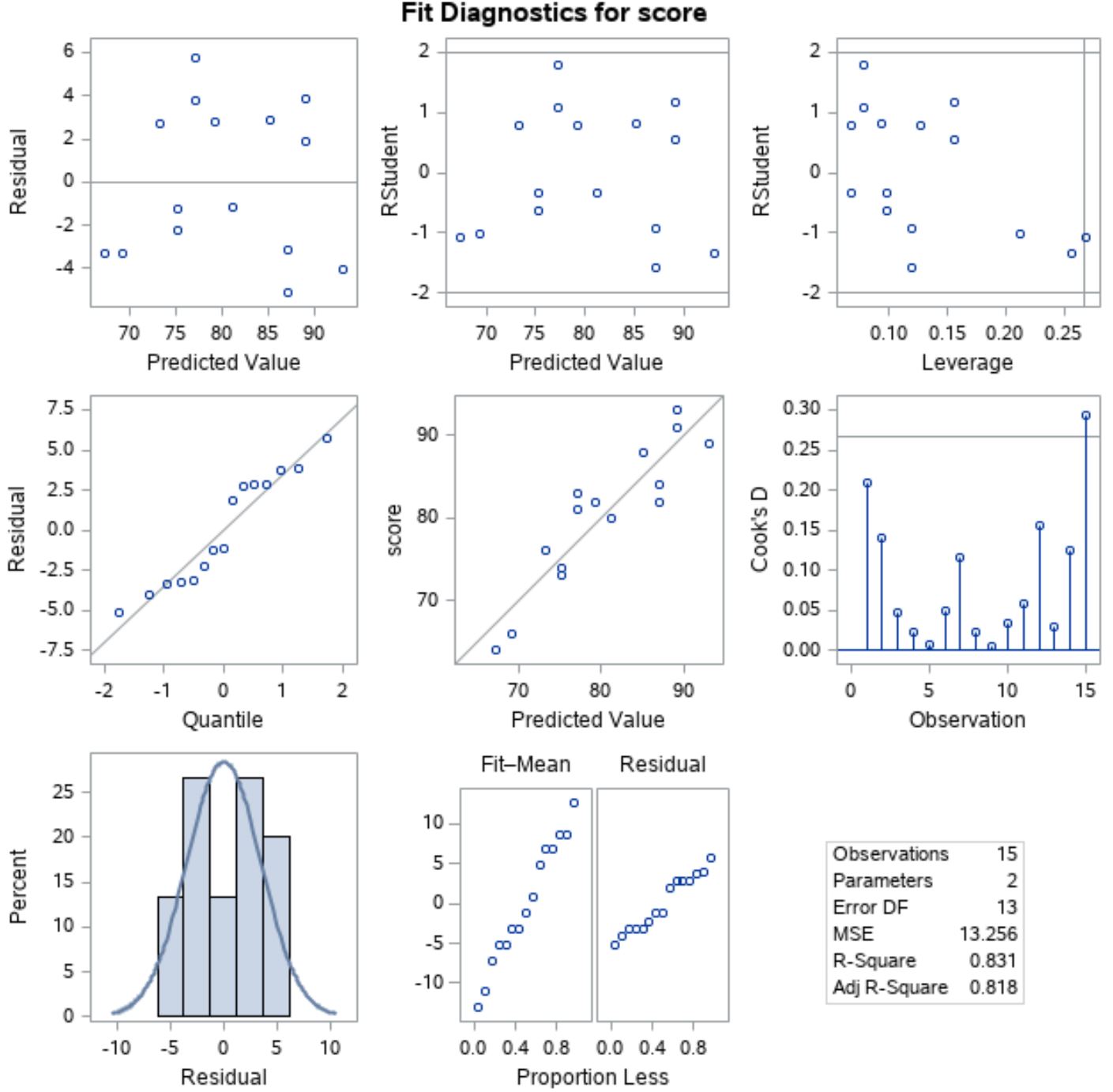
Untuk memverifikasi bahwa residu berdistribusi normal , kita dapat menganalisis plot di posisi kiri garis tengah dengan “Kuantil” di sepanjang sumbu x dan “Sisa” di sepanjang sumbu y.

Plot ini disebut plot QQ , kependekan dari “quantile-quantile”, dan digunakan untuk menentukan apakah suatu data berdistribusi normal atau tidak. Jika data berdistribusi normal, titik-titik pada plot QQ akan terletak pada garis lurus diagonal.

Dari grafik kita dapat melihat bahwa titik-titik tersebut terletak kira-kira sepanjang garis diagonal lurus, sehingga kita dapat mengasumsikan bahwa residunya berdistribusi normal.

Selanjutnya untuk memverifikasi bahwa residunya homoskedastis , kita dapat melihat plot di posisi kiri baris pertama dengan “Nilai prediksi” di sepanjang sumbu x dan “Sisa” di sepanjang sumbu y.

Jika titik-titik plot tersebar secara acak di sekitar nol tanpa pola yang jelas, maka kita dapat mengasumsikan bahwa residunya bersifat homoskedastis.

Dari plot tersebut terlihat bahwa titik-titik tersebar di sekitar nol secara acak dengan variansi yang kurang lebih sama pada setiap level di seluruh plot, sehingga dapat diasumsikan bahwa residunya bersifat homoskedastis.

Karena kedua asumsi terpenuhi, kita dapat berasumsi bahwa hasil model regresi linier sederhana dapat diandalkan.

Sumber daya tambahan

Tutorial berikut menjelaskan cara melakukan tugas umum lainnya di SAS:

Cara melakukan ANOVA satu arah di SAS
Cara melakukan ANOVA dua arah di SAS
Cara menghitung korelasi di SAS