Cara melakukan regresi loess di r (dengan contoh)

Regresi LOESS , terkadang disebut regresi lokal, adalah metode yang menggunakan penyesuaian lokal untuk menyesuaikan model regresi dengan sekumpulan data.

Contoh langkah demi langkah berikut menunjukkan cara melakukan regresi LOESS di R.

Langkah 1: Buat datanya

Pertama, mari buat bingkai data berikut di R:

 #view DataFrame
df <- data. frame (x=c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14),
                 y=c(1, 4, 7, 13, 19, 24, 20, 15, 13, 11, 15, 18, 22, 27))

#view first six rows of data frame
head(df)

  xy
1 1 1
2 2 4
3 3 7
4 4 13
5 5 19
6 6 24

Langkah 2: Sesuaikan beberapa model regresi LOESS

Kita dapat menggunakan fungsi loess() untuk menyesuaikan beberapa model regresi LOESS ke kumpulan data ini, menggunakan nilai berbeda untuk parameter span :

 #fit several LOESS regression models to dataset
loess50 <- loess(y ~ x, data=df, span= .5 )
smooth50 <- predict(loess50) 

loess75 <- loess(y ~ x, data=df, span= .75 )
smooth75 <- predict(loess75) 

loess90 <- loess(y ~ x, data=df, span= .9 )
smooth90 <- predict(loess90) 

#create scatterplot with each regression line overlaid
plot(df$x, df$y, pch= 19 , main=' Loess Regression Models ')
lines(smooth50, x=df$x, col=' red ')
lines(smooth75, x=df$x, col=' purple ')
lines(smooth90, x=df$x, col=' blue ')
legend(' bottomright ', legend=c(' .5 ', ' .75 ', ' .9 '),
        col=c(' red ', ' purple ', ' blue '), pch= 19 , title=' Smoothing Span ')

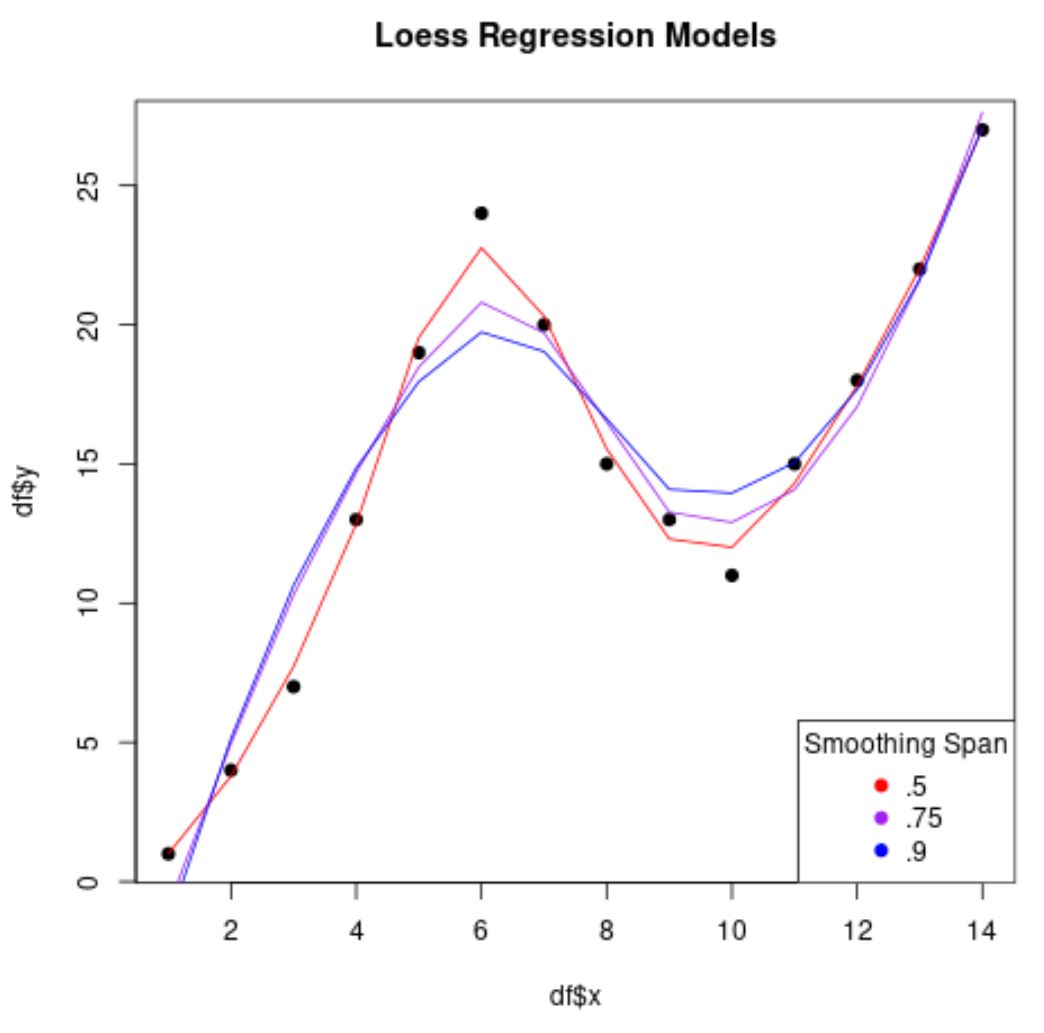
Perhatikan bahwa semakin rendah nilai yang kita gunakan untuk span , semakin tidak “mulus” model regresinya dan semakin besar upaya model untuk menyesuaikan titik data.

Langkah 3: Gunakan K-Fold Cross-Validation untuk Menemukan Model Terbaik

Untuk menemukan nilai jangkauan optimal yang akan digunakan, kita dapat melakukan validasi silang k-fold menggunakan fungsi dalam paket tanda sisipan :

 library (caret)

#define k-fold cross validation method
ctrl <- trainControl(method = " cv ", number = 5 )
grid <- expand. grid (span = seq( 0.5 , 0.9 , len = 5 ), degree = 1 )

#perform cross-validation using smoothing spans ranging from 0.5 to 0.9
model <- train(y ~ x, data = df, method = " gamLoess ", tuneGrid=grid, trControl = ctrl)

#print results of k-fold cross-validation
print (model)

14 samples
 1 predictor

No pre-processing
Resampling: Cross-Validated (5 fold) 
Summary of sample sizes: 12, 11, 11, 11, 11 
Resampling results across tuning parameters:

  span RMSE Rsquared MAE      
  0.5 10.148315 0.9570137 6.467066
  0.6 7.854113 0.9350278 5.343473
  0.7 6.113610 0.8150066 4.769545
  0.8 17.814105 0.8202561 11.875943
  0.9 26.705626 0.7384931 17.304833

Tuning parameter 'degree' was held constant at a value of 1
RMSE was used to select the optimal model using the smallest value.
The final values used for the model were span = 0.7 and degree = 1.

Terlihat bahwa nilai span yang menghasilkan nilai root mean square error (RMSE) terendah adalah 0.7 .

Jadi, untuk model regresi LOESS terakhir kita, kita akan memilih untuk menggunakan nilai 0,7 untuk argumen span dalam fungsi loess() .

Sumber daya tambahan

Tutorial berikut memberikan informasi tambahan tentang model regresi di R:

Cara melakukan regresi linier sederhana di R
Cara melakukan regresi linier berganda di R
Bagaimana melakukan regresi logistik di R
Bagaimana melakukan regresi kuantil di R
Bagaimana melakukan regresi tertimbang di R