Regresi logaritma
Artikel ini menjelaskan apa itu regresi logaritma dan bagaimana cara kerjanya. Selain itu, Anda dapat melihat contoh regresi logaritmik untuk memahami konsepnya sepenuhnya.
Apa itu regresi logaritma?
Regresi logaritma adalah model regresi yang memasukkan logaritma dalam persamaannya. Secara khusus, dalam regresi logaritma, logaritma variabel independen diambil. Jadi persamaan model regresi logaritma adalah y=a+b·ln(x).
Regresi logaritmik sangat berguna untuk menyesuaikan model regresi ketika data sampel membentuk kurva logaritmik, sehingga model regresi lebih cocok dengan data sampel. Di bawah ini kita akan melihat kapan Anda harus melakukan regresi logaritmik.
Jadi, regresi logaritmik merupakan salah satu jenis regresi nonlinier, sama seperti regresi eksponensial dan regresi polinomial.
Rumus Regresi Logaritma
Model regresi logaritma melibatkan pengambilan logaritma variabel independen. Oleh karena itu, rumus persamaan regresi logaritma adalah y=a+b·ln(x).
![]()
Emas:
-

adalah variabel terikat.
-

adalah variabel independen.
-

adalah koefisien regresi.
Perhatikan bahwa y=a+b·ln(x) sebenarnya adalah persamaan garis, namun alih-alih mengacu pada variabel asal x dan y, ia mengacu pada variabel ln(x) dan y.
Kapan melakukan regresi logaritma?
Regresi logaritmik perlu dilakukan jika grafik data sampel berbentuk kurva logaritma, yaitu jika plot titik-titiknya mirip dengan grafik fungsi logaritma.
Lihat diagram sebar di bawah, model regresi linier telah dipasang ke kumpulan data. Seperti yang Anda lihat, garis bukanlah perkiraan data yang buruk, namun jika Anda berhati-hati, nilainya meningkat lebih cepat di awal grafik daripada di akhir, sehingga garis tersebut tidak sepenuhnya sesuai dengan pengamatan. .
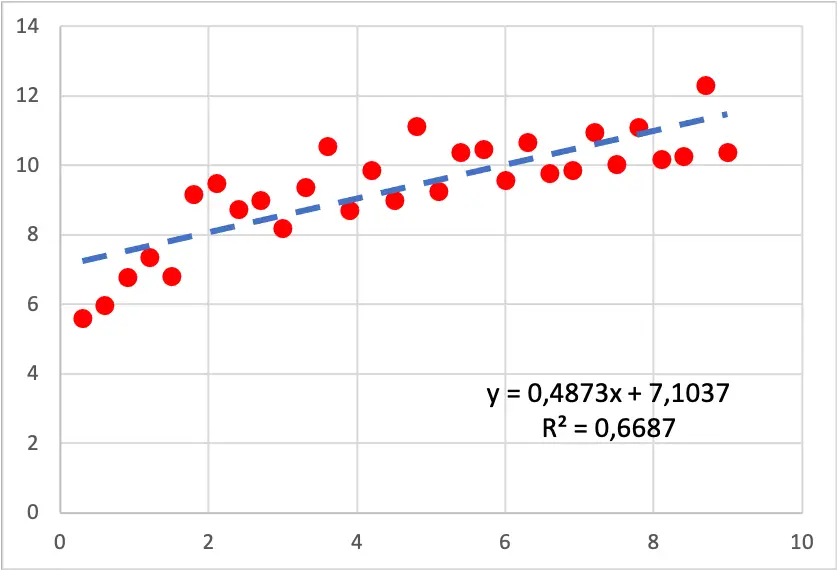
Jadi ada baiknya mencoba membuat model regresi logaritmik, karena datanya terlihat mengikuti kurva logaritmik. Hasil yang diperoleh dari model regresi logaritmik adalah sebagai berikut:

Seperti yang Anda lihat pada grafik sebelumnya, model regresi logaritmik yang dihasilkan lebih sesuai dengan data sampel. Faktanya, koefisien determinasi meningkat dari 66,87% menjadi 80,05%, sehingga model kini dapat menjelaskan data sampel dengan lebih baik. Oleh karena itu, dalam hal ini sebaiknya menggunakan regresi logistik untuk mencari persamaan yang mendekati nilai data.
Jenis regresi nonlinier lainnya
Tiga kasus regresi nonlinier yang paling umum adalah:
- Regresi logaritma : diambil logaritma variabel bebasnya.
- Regresi eksponensial : Variabel independen adalah eksponen persamaan.
- Regresi Polinomial : Persamaan model regresi berbentuk polinomial.